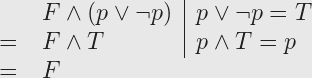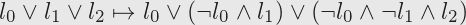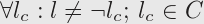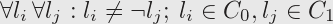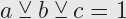DOGgy Style Programming
| Author: | Wolfgang Scherer |
|---|
Doggy style commonly refers to performing an act, highly focused on a part of yourself that eludes conscious control, with minimal coordinating support by other senses, affecting your mind in wondrous and mysterious ways. Or in a nutshell: Doing something without actually knowing what you're doing.

Contents
Contents
- Contents
- Introduction
- Problems
- Logic
- The Wonders of Single Selection
- So what now?
- Satoku - The Game
- Design Principle
- Independent Set Problem and Adjacency Matrix
- Satoku Matrix
- Satoku Matrix Properties
- Requirements Update Algorithm
- Other Operations
- Conflict Maximization
- Merging Clause Sub-Matrixes
- Conflict Comparison
- Clause Reduction By Redundancy Removal
- Cross Clause Requirements
- Alternate Clause Representations
- Reverse Mapping of a Satoku Matrix
- 1,2,k-SAT, soft, hard, weak and strong
- Making Decisions
- Logical Reasoning
- Undriven Clause Learning
- 3,4-SAT Splitting
- Informed Decisions
- Advantages
- Obfuscated XOR Structure
- Per-Problem Worst Case Upper Bound
- Summary
- Mathematical Theories
- Data Is Amorphous
- Programming Techniques
- Documentation
- Template Languages
- Unit Tests
- Libraries
- IDE
- Expert Systems
- Footnotes
- References
Introduction
The picture above is an activity diagram, showing a DOGgy style programmer fiercely tackling a problem, which appears to be pretty unimpressed by these efforts. The programmer's boss and customers are obviously quite surprised by the unexpected course of events.
DOG is actually meant to stand for Delusions Of Grandeur. However, the reference to the animal seems fitting, too.
Dogs are said to have bad eyesight but can smell exceptionally well which implies certain limitations in their perceived reality. For instance, a person's visual appearance often arrives before their smell in a dog's field of perception. In that case a dog barks at the perceived threat before realizing that it's actually a friendly entity. This could account for the joy expressed by dogs, which might seem unusually exaggerated for a being with better eyesight than sense of smell. However, considering the initial fear and subsequent relief of a dog, it appears perfectly normal[1].
This example is meant to illustrate the irreconcilable differences between the perceptive realities of normal people and DOGgy style programmers. The communication is often conflicted.
Back on topic, let me assert that a DOGgy style programmer has a good amount of delusions of grandeur and that it is both essential for and detrimental to performing a programming task.
Theorem: The central axiom of DOGgy style programming comes from the book The Mythical Man-Month: Prepare to do it twice. In the context of DOGgy style programming, this is a demand, not a proposition. And it is a recursive statement, which also holds for the second and further turns.
Theorem: DOGgy style programming asserts and demands that everthing is always finished. You will always be interrupted, and never come back to continue what you started. If you do come back, you will have forgotten what the whole matter was about, including what you were planning to do. Always look at your program and consider that this is as good as it gets. Add some hints for your future self, if you're not satisfied right then.
Theorem: The principle of included middle: Balance you must find, young warrior!, Yoda says, and so DOGgy style programming demands.
All principles also apply to this treatise. Don't try to understand it the first time. Take, what is useful for you, skip what is boring, and come back later (or not), to get some more. Since this is itself an exercise in DOGgy style programming and already the n-th incarnation in the never ending preparation cycle, chances are that I have added some more.
Applying the second priniciple leads to the conclusion that you will no longer be able to find this page when you do intend to come back, so you best take everything you can.
Chances are, that I will not be able to find this page anymore on my harddrive, or that I have completely forgotten about it. And therefore, this is as good as it gets and nothing will ever be added. So don't be disappointed.
Warning
It may take a streak of self-irony to understand this guide. Otherwise, it could appear offending and be detrimental to your mental health[2].
Problems
The main task of a programmer consists of solving problems.
Mathematicians believe that logical problems (3-SAT) generally have exponential worst case behavior. Some special cases, however, can be solved in polynomial time. E.g., XOR-SAT problems can be mapped to linear equations which can be easily solved by Gaussian elimination.
It surely requires delusions of grandeur to even consider solving any non-trivial problems, let alone in a timely manner.
Solving problems involves a good deal of logic (see Logic - By Branch / Doctrine - The Basics of Philosophy for an introductory overview) and almost no mathematics, except combinatorics (unless your problem is mathematical, then you need a lot of mathematics).
I do not think mathematics is useless -- quite to the contrary -- but I disagree on its universal usefulness for solving problems. I have found logic, general semantics and cybernetics far more helpful than mathematics.
While mathematics appears to a DOGgy style programmer like the drug of a tautology-junkie suffering from symmetry-OCD, DOGgy style appears to a mathematician like the life-style of a sloppy hobo who cannot even get his facts straight.
However, appearances can be deceiving, and despite its appearance, DOGgy style programming is a serious and balanced process, which cannot simply be simulated with sloppiness. It takes years of devoted practice and failed discipline to master this programming style. Most of the time is spent examining various other processes that claim to be easier to learn, to have better results, and generally be the one true way into the light.
Since beginners will have to apply the other processes anyway, they may as well start with them and collect the necessary experience on the way. However, beginners can still get some guidance here on how to avoid the dangerous endless loop of "I have done it for so long, therefore it must be right."
Lemma: Applying Occam's razor too early can seriously damage your program. Cutting away properties which you have no immediate use for can lead to dead ends in later stages of a project. It really is easier to cut away stuff, after you actually find out what you are doing.
Corollary: Resist the temptation of unnecessary decision-making. This is not good DOGgy style practice. Always be aware, that mighty logicians (with brighter minds than yours) have still not found a universally accepted resolution for the problem of future contingents.
The assumption that since a matter has to be decided eventually, it is therefore necessary that it be decided right now is a logical fallacy.
Logic
Is not the same as mathematics. Believing that the symmetries of mathematics are the most useful applications of logic is a serious case of delusions of grandeur.
Lemma: Most problems come AS IS[3] and do not fit any single mathematical model. Whatever is available should be used, as long as it fits at least loosely. If the model must be modified to make it fit, then change it. Avoid changing the problem to fit the model. Model whatever you know. Do not model, what you do not know (yet), but do identify what you don't know!
My very own personal delusions of grandeur regarding logic appeared by thinking for 25 years, that there would be nothing new and surprising in the field of propositional logic for me.
Until someone gave me a book about NP-completeness with the words:
Whenever I come across a problem [like yours] that is contained in this book, I realize, that it does not make any sense to try and solve it.
And so I ventured to find out why.
Unary Logic Functions
Let's have a look at unary logic functions. There are exactly four of them (this is a very useful application of combinatorics):
| p | F0 | F1 | F2 | F3 |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
These functions can be described as follows:
| F0 | Contradiction | F |
| F1 | Identity, Single Selection, Multiple Selection | p, X1(p), MS(p) |
| F2 | Negation | ¬p |
| F3 | Tautology | T |
- X1 stands for single selection (exactly one selection must be made, i.e. exactly one of the variables must be true).
- MS stands for multiple selection (one ore more selections must be made, i.e. one ore more of the variables must be true).
Lemma: The correct representation of unary logic function F0 would be F0,1 -- but DOGgy style allows to have faith in the ability of the reader to understand the concept of context.
In this case, there is no need within a section about unary functions to redundantly identify all functions as unary. (It's implicit, dummy.)
Binary Logic Functions
Let's have a look at binary logic functions. There are exactly 16 of them (another useful application of combinatorics):
| p | q | F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | F15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
These functions can be described as follows:
| F0 | Contradiction | |
| F1 | Conjunction | AND |
| F2 | ¬(p → q) | |
| F3 | p | |
| F4 | ¬(¬p → q) | |
| F5 | q | |
| F6 | Antivalence, Single Selection | XOR, X1 |
| F7 | Disjunction, Multiple Selection | OR, MS |
| F8 | NOR | |
| F9 | Equivalence | IFF p THEN q |
| F10 | ¬q | |
| F11 | ¬p → q | |
| F12 | ¬p | |
| F13 | Implication | IF p THEN q |
| F14 | NAND | |
| F15 | Tautology |
Hmm, besides the selection thingies, not much new.
Ternary Logic Functions
Ternary logical functions are defined by subsequent application of the binary function to the result of the binary function and the next logical value, e.g.:
OR(p, q, r) = ((p OR q) OR r) F127,3(p, q, r) = F7,2((F7,2(p, q), r)
Generally, any n-ary logic function can be recursively broken down to repeated applications of the binary version:
f[n] ( v0, .., v[n-1] ) = f[2] ( f[n-1] ( v0, .., v[n-2] ), v[n-1] )
Now, isn't that nice! All those theorems and lemmas and transitivities and distributivities and symmetries, you name it! And then there is no need to examine all those n-ary functions in a truth table, it's just great! Logic seems very mathematical indeed.
I should not have been surprised, when I discovered that I was using antivalence (XOR) and single selection (X1) interchangeably (which is correct in binary contexts only).
Lemma: DOGgy style predicts, that you will keep confusing similar but not identical concepts for quite some time before realizing that there is a difference.
The difference is that n-ary single selection cannot be broken down to a binary single selection applied to the result of an (n-1)-ary single selection and a truth value:
F105,3(p, q, r) == F6,2(F6,2(p, q), r) # XOR F104,3(p, q, r) != F6,2(F6,2(p, q), r) # X1
It is possible to define a quasi-ternary logic, to be used for intermediate results, which allows to process n-ary single selections in the usual manner. Here 1 stands for true and 0, -1 both stand for false. But I am not sure whether that helps :).
| p | q | FX2 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | -1 | -1 |
| 1 | 0 | 1 |
| 1 | 1 | -1 |
| 1 | -1 | -1 |
| -1 | 0 | -1 |
| -1 | 1 | -1 |
| -1 | -1 | -1 |
F104,3(p, q, r) = FX2(FX2(p, q), r) > 0
If you present someting like this, you will immediately arouse heated excitement (and not of the good kind). You are mixing boolean operators with arithmetical operators. It does not matter, that your programming language allows you to do so and that it is therefore a correct model of what your program does. It is still forbidden, since you have not explicitely stated, that you are talking Programmese. And it is also forbidden to take other people's hard work and deface in such an apalling way. You are hereby expelled from the calculus. Nothing you say makes any sense at all!
Lemma: In DOGgy style programming it is always a good idea to mention very early on, that you are using Programmese to describe the features of your program. If need be, contact me and I will set up a Bitbucket project about the promising ongoing research in Programmese, which will state that a formalized theory will be presented real soon. This will not only protect you from attacks, but it will elicit the impression that you are on the bleeding edge of the next best hype in computer science.
So, the interesting ternary functions regarding selection are these:
| p | q | r | F104 | F105 | F127 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 |
The functions can be described as follows:
| F104 | Single Selection | X1 |
| F105 | Antivalence | XOR |
| F127 | Disjunction, Multiple Selection | OR, MS |
The Wonders of Single Selection
Single selection "hides" for a while behind other logical functions[4]:
- Single selection is equivalent to the identity F2,1 (multiple selection) in a unary context.
- Single selection is equivalent to F6,2 (XOR) in a binary context.
- It only appears as something completely different in a ternary context as F104,3.
Let me illustrate, why this lack of knowledge cost me about 4 years of hobby-time fiddling with SAT, before it became unavoidably obvious to me, that the corresponding selection problem is in no way the same as the decision problem. (The way I finally found out would rather be a good theme for a Monty Python movie).
Lemma: In DOGgy style programming it is dumb to dismiss different perspectives to a problem, because somebody else says that it is useless. But keep in mind, that getting it right the first time deprives you of the deeper knowledge gained by being dumb and finding out why after the fact. But do not worry, the universe will give you plenty of opportunities to enjoy the cathartic experience of finding out that you have been dumb.
Historic Context
Note
Despite their titles, this and the next section merely illustrate the merits and pitfalls of ranting and other bad practices.
Except for the statement about the equivalence of multiple selection and OR, they do not contribute anything essential.
Before talking about SAT-problems, I would like to limit the expectations in regard to that matter (beware of DOG!).
At the time when I started fiddling with SAT problems (around 2004), the available material still cited the worst case for a brute-force attack:
"It takes worst case exponential time (2^n) over the variables, if there is only a single solution (or no solution at all), and if that solution (contradiction) is found last[5]."
| [1] | Have you ever played Sudoku? The funny thing about Sudokus is, that they all have a single solution. I once mapped a Sudoku to a SAT problem and found that it was pretty impressive:
After trivial resolution the following clauses remained: // clauses: 1105 // max literal count: 17 After mapping to satoku matrix: // clauses: 319 // 2-SAT clauses: 140 // k-SAT clauses: 179 |
I was under the impression, that it must be a lot harder to find all solutions. And since I was looking for a hobby to last me a lifetime, I thought that it would make no difference just how unsolvable the problem is. In order to understand the structure of a problem, I decided it was best to acquire as much information as possible and went with trying to find all possible solutions instead of just a single one.
I did not set out to prove P vs. NP or be the fastest kid on the block. I was just curious, whether I could get a clue as to why that problem was so hard.
Since my goal was different from the standard research in this field (and since I cannot understand mathematical texts so well), I did not do a lot of research. Instead I wrote programs to visualize the problem structure and explore various algorithms.
The purpose of the programs I wrote is to facilitate analysis of logical k-SAT problems. The exponentiality is still there, I just have a much better idea why that is so. And I have a tool to perform logical reasoning in a geometrically structured environment without the symbolic clutter of algebraic symbols.
The satoku matrix scales well from 1-SAT to k-SAT and back, and it delivers a polynomial time 2-SAT solver without the need to search for a solution. That is aesthetically especially nice. (I.e., I like my program better, but who wouldn't :)).
I find it funny, that it turns out to be actually slightly more efficient to find a single solution when searching for all possible solutions simultaneously, than it is when searching for a single solution only.
The current state of affairs allows me to get a good upper bound on the worst-case running time per individual problem, so that I can display the message "No need to get up" or "You can go on a nice trip to Hawaii". This is good, since you are supposed to always give progress feedback to the user.
Lemma: If you feel the need to explain yourself -- as most DOGgy style programmers do as a pastime -- you should consider bringing that up at your next PA (Programmers Anonymous) meeting. If you cannot suppress the urge to do it right there and then, at least consider putting the stuff in a footnote or an appendix. It's just boring for everybody else and does not change the facts. But thanks for sharing.
Course of Events
Satisfiability problems are sometimes defined in a manner as in the following citation from 2-satisfiability on Wikipedia (emphasis added by me):
The 2-satisfiability problem is to find a truth assignment to these variables that makes a formula of this type true: we must choose whether to make each of the variables true or false, so that every clause has at least one term that becomes true.
I had read that "each SAT problem gives rise to a similar selection problem, which is again NP-complete"[someone]. I misunderstood this as a selection problem being the same problem and the at least to stand for multiple selection[6]:
Select (multiple) literals from clauses so that at least one of them is true.
The proper form is to demand that exactly one literal must be selected from each clause (single selection), so that no two selected literals represent a variable and its negation.
Although the assignment of a truth value may seem implicit, there is no necessity to do so. (It will later become obvious, why it is a good thing, that actual assignment can be deferred indefinitely).
It is obvious, that the condition for proving satisfiability for a selection problem can be met without actually making any truth value assignment. Even, if the implict assignment of True to a selected variable:
literal = variable → variable = T
or False to a selected negated variable:
literal = ¬variable → variable = F
is accepted, that still leaves cases where it is it not necessary to select all of the variables.
In the trivial case, where all variables only appear once in a formula, it is even impossible to make a satisfying selection which contains all variables. E.g.:
(a ∨ ¬b ∨ c) ∧ (d ∨ e ∨ ¬f)
Fun fact: in this case, it is not even necessary to make any selection or assignment. Since there are no conflicts, all assignments satisfy the problem.
However, once such a partial core-assignment is found, all fully assigned solutions that statisfy the multiple selection property can be trivially derived through permutations[7] of the possible truth values over the remaining unassigned variables.
The statement "Formula X is satisfiable" becomes true, as soon as the single selection condition is met. The assignment of thus far unassigned variables does no longer have an influence on that truth value[8].
In other words: It is possible, that a fully assigned solution cannot be presented by single selection. Nonetheless, it is certain, that a fully assigned solution can eventually be constructed and that it will take at most linear time over the set of unassigned variables to do so.
The fact that it is necessary to assign all variables for a complete assignment of truth values is completely off-topic. Even for the decision problem variant, a partial assignment is already sufficient to check the validity of the prospective fully assigned solutions: If there is any true assignment present in a clause, the condition at least is already satisfied. No reason to demand more[9].
What is the reason behind the demand, that all variables must be assigned? The principle of excluded middle? Logicians can only count to 1? My computer ran out of numbers? I could not find a class in Java? Too much effort, maybe?
If 1 represents true, 0 represents false and -1 represents unassigned, then the following algorithm correctly checks the validity of a partially assigned solution (it also works, if all variables are assigned):
good = False # I cannot remember whether an empty clause set
good = True # signifies True or False \|:todo:|
# So I go with: `Is a non-existent problem satisfiable`? A: yes
for i in range(len(clauses)):
clause = clauses[i]
good = False
for j in range(len(clause)):
if clause[j] == 1:
good = True
break
if not good:
break
if good:
print("SAT")
else:
print("UNSAT")
This algorithm does exactly, what the definition of the problem demands for verifying a solution. I have to admit I'm stumped.
Lemma: In DOGgy style programming it is true, that Thou shalt not rant!. Remember principle 3 of DOGgy style programming. As RMS once pointed out:
Criticizing the flaws of other people's thinking about the problem does not help me understand the problem or your solution. So it is best to leave that out.
Or bring it up at your PA meeting.
Corollary: Ranting usually means, that you have not fully understood a mechanism. Wait a while until it becomes clear. If ranting helps you to bide your time, feel free to do so. However, you should not publish the rant, but rather replace it with the enlightenment you have found. In this special case, you can keep the rant to demonstrate the principle.
Corollary: Try to find out, why you don't understand it. What is the context of the statement[10]? Maybe ask somebody else.
Lemma: However, this example is still useful to show why in DOGgy style programming you must not fall prey to decision-making-OCD. All decisions must be procrastinated until they are absolutely necessary. And even then, you should rather spend your time with making excuses for not yet deciding, than acting against that gut-feeling that still tells you that the decision is potentially dangerous. Good half-truths are always: "The code needs to be cleaned up", "An important part of the program needs attention, because it can still turn the whole project into a failure".
Experience shows, that right after you irrevocably made the decision and cleaned up your program in many places, you will all of a sudden realize in clairvoyant brilliance why it was dumb to make the decision the way you made it. You will blush and your gut-feeling will smirk (again): "told you so!"
Corollary: This leads directly to the rule, that in DOGgy style programming you must never ever work without version control. No matter how much other people insist on it not being necessary when you work on your own. This is their own varition of delusions of grandeur, that you must never deal with.
Lemma: Gut-feeling (or intuition) is a central part of DOGgy style programming. It is the part of yourself that eludes conscious control and the driving force behind DOGgy style programming. Therefore, DOGgy style programming can never be a conscious process and no rigid model can ever be constructed. But you must never stop to try, since the journey is the destination.
As multiple selection turns out to be just another name for a disjunction (OR), I will refer to single selection (X1) as simply selection from here on out (and maybe above, if I forget, that plain selection is not supposed to appear before this point, or as I'm sure to forget, that I must move this paragraph to the beginning.) (|:todo:| don't! This TODO serves as a perfect example for a bad TODO. The requested action should have happened immediately).
So what now?
Single selection is pretty boring in itself. No nice formulas, no nice other thingies, no fields, rings, groups, no theorems, no nix[11]. But it is nonetheless used for selection problems. To show its usefulness, let's design an algorithm to better understand the structure of SAT problems.
I have no idea, whether any of this is generally known or not, but I checked n-tuple times that everything is correct and that the reasoning is sound. However, I know by far not enough mathematics to be able to express my thoughts in generally accepted mathematical terms[12].
Therefore my findings are presented AS IS in the hope that they will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
Satoku - The Game
Although a game of Satoku can be played entirely with pencil and paper, it is best played in Emacs with satoku-mode. (Get satoku.el, see Satoku README for basic instructions).
The examples from this article are included in the package to make it easier to follow the argument.
Design Principle
The design principle for this algorithm is based on the concept of strong decisions and weak decisions, where
- a strong decisions is a decision that never has to be reversed
- a weak decision is a decision that possibly needs to be reversed (backtracking).
The goal of the algorithm developed here is to avoid weak decisions as long as possible and still provide a useful tool for structural analysis of boolean satisfiability problems.
Independent Set Problem and Adjacency Matrix
As shown in David M. Mount, CMSC 451 Lecture Notes, Fall 2012[13], pp. 92, a 3-SAT problem can be mapped to an independent set problem in polynomial time.
Before I found this proof, I illustrated the principle with a game called Pick-A-Puck (I should have used an undirected graph, but I did not know too much about graph theory).
Lemma: If you do proper research and talk to the right people, you can save a lot of time and effort. You will also find out, what the rest of the world accepts as proof and what not. DOGgy style programming ist not about sloppiness! It is about efficiency!
The mapping to an independent set problem ensures, that only one literal can be selected from each clause. (Not so) coincidentally that is excatly what the single selection function requires.
Independent set problems can further be mapped to an adjacency matrix, which can be inverted directly during mapping by exchanging 0 and 1.
Mapping the following CNF 3-SAT formula:
(¬a ∨ ¬b ∨ c) ∧ (¬a ∨ b ∨ ¬c) ∧ (¬a ∨ b ∨ c) ∧ ( a ∨ ¬b ∨ ¬c) ∧ ( a ∨ ¬b ∨ c) ∧ ( a ∨ b ∨ ¬c) ∧ ( a ∨ b ∨ c)
to an inverted adjacency matrix looks like this:

You could now go ahead and use algebraic methods on this construct, or whatever it is, that is available for this structure (I should do some research one of these days). Or you can choose to go another route.
Lemma: DOGgy style programming is all about choice and pleasing someone (if not the customer, than at least yourself). If you can support different possiblities at minimal cost, you should always do so, no matter whether it is currently needed or not.
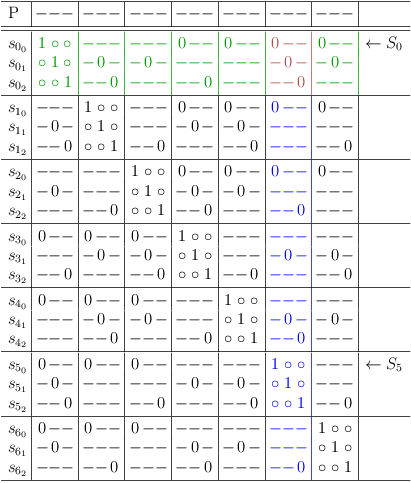
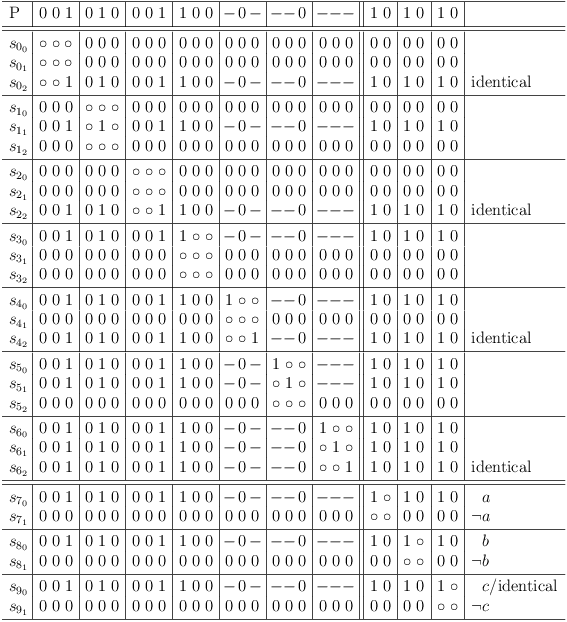
Satoku Matrix
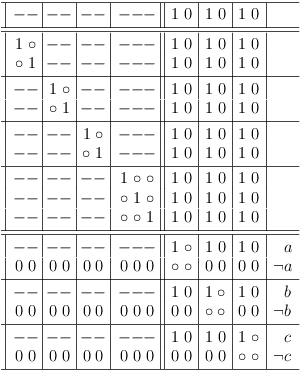
The inverted adjacency matrix of the independent set graph does not show the clause restrictions, which were explicitly introduced during the mapping (and are therefore implicit in the final inverted adjacency matrix). However, the information is readily available during mapping and allows to subdivide the matrix into regions, which clearly indicate the relation of the matrix to the mapped clauses:

This augmented inverted adjacency matrix is called satoku matrix (SM) to clearly indicate, that the algorithm is unrelated to graph theory. Whether graph theory does or does not apply beyond the basic property of mapping a SAT problem correctly to an (inverted) adjacency matrix is outside the scope of this discussion.
Lemma: In DOGgy style programming, when something acquires different properties (be they substantial or merely oranmental), it must get a new name to avoid ambiguities. You can always call it XXX or use the placeholder system of your choice, if you cannot think of a name right now.
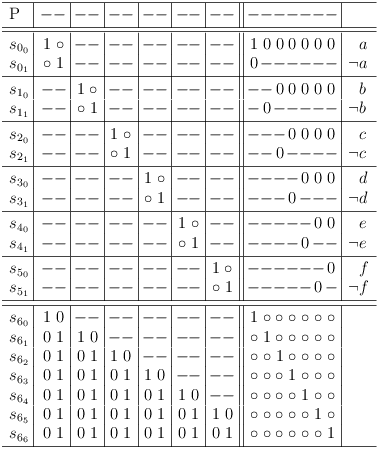
In the context of selection rows, a matrix cell is denoted as c[[i, j], [f,g]] corresponding to selection rows s[i,j] and s[f,g].
The truth value instances of 1 in the SM{} are classified based on the number of occurrences in a clause segment of a selection row.
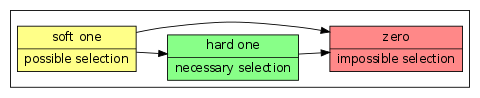
- If a clause segment in a selection row contains more than one matrix cell with the value 1, the values are replaced by a dash (-) and called soft one. Note that the truth value of a soft one is still 1, the substitution is merely ornamental.
- If a clause segment cs[[i,j], f] in a selection row s[i,j] contains exactly one matrix cell c[[i,j], [f,g]] with the value 1, the value is unchanged and called a hard one. The corresponding selection row s[f,g] becomes a required (or necessary) selection for selection row s[i,j].
After these rules are applied, the satoku matrix looks like this:
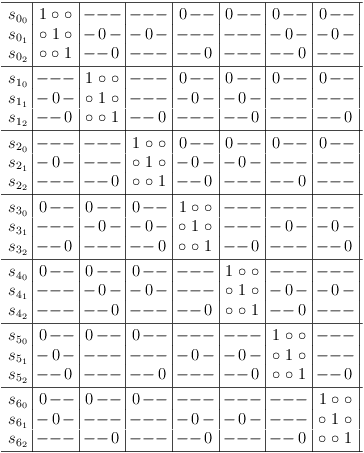
For a better overview, a status row, representing the selection status of the entire problem is introduced. It is labeled P and behaves essentially like a matrix row. If an entire column of the satoku matrix becomes 0, the corresponding cell in the status line also becomes 0:
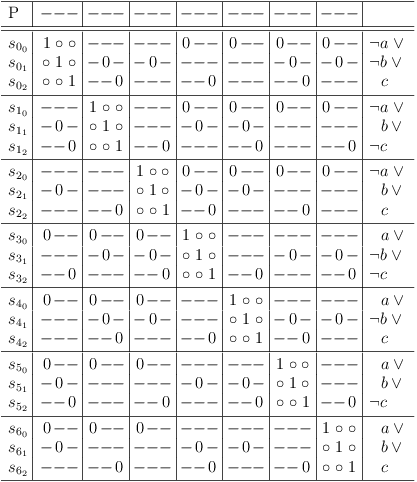
Finally, the original SAT problem is augmented with some tautologies to represent the (possible) selection of either a variable or its negation[14]:
(¬a ∨ ¬b ∨ c) ∧ (¬a ∨ b ∨ ¬c) ∧ (¬a ∨ b ∨ c) ∧ ( a ∨ ¬b ∨ ¬c) ∧ ( a ∨ ¬b ∨ c) ∧ ( a ∨ b ∨ ¬c) ∧ ( a ∨ b ∨ c) ∧ ( a ∨ ¬a) ∧ ( b ∨ ¬b) ∧ ( c ∨ ¬c)
Proof: For all propositional formulas F the following statement is true:
Lemma: In DOGgy style programming proofs are way cool! Give them, if you can. But don't worry too much about them. If your program works, there is no need to prove it.
Since these tautologies are entirely optional, they are separated from the original core problem (upper left matrix region) by a double line.
So the final satoku matrix looks like this:
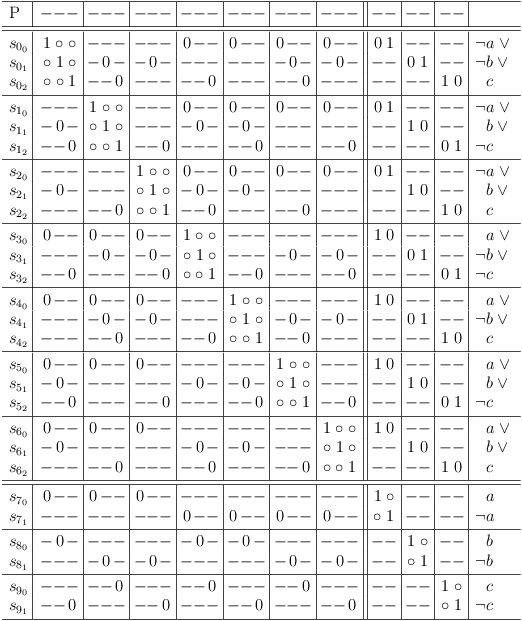
A dash (-) is merely a substitution for the truth value 1, if there is more than one matrix cell containing the value 1 present in a clause segment of a selection row.
A selection row is an entire satoku matrix row, which represents a selection from a clause of the mapped SAT problem including the dependencies on all other selections.
The selection row indexing
refers to literal j from clause i of the mapped SAT problem.
satoku matrix subdivisions limited by horizontal lines represent clause sub-matrixes S[i], containing one or more selection rows.
Clause sub-matrixes are further divided by vertical lines into clause conflict sub-matrixes S[i, f], where f has the same range of values as i.
A clause conflict sub-matrix S[i, f] represents the dependencies between all selections from two SAT problem clauses S[i] and S[f].
The special clause conflict sub-matrix S[i, i] is called clause identity sub-matrix.
A clause segment cs[[i,j], f] is the intersection of selection row s[i,j] and clause conflict sub-matrix S[i,f].
The row labeled P is not part of the matrix, it shows the status of globally possible (- or +), required (1) and impossible (0) selections.
The double lines are just visual aids to separate semantically different groups (e.g., core problem clauses and variables). They have the same meaning as a single line.
The right margin is used for comments which can be completely ignored.
Do you remember, that the clauses are mapped to single selection clauses and that single selection is equivalent to XOR in a binary context? So the additional variable clauses can also be read (sel(p) XOR sel(¬p)) in the context of the satoku matrix.
Lemma: If you are suffering from instant-cleanup-OCD or everything-must-have-a-purpose-OCD, unnecessary things are thrown away. However, in DOGgy style we never throw anything away, even if we do not (yet) know, whether it is useful or not (it does at least visualize a concept in this case). If we do not know all facets of the problem yet, it may come in useful later on.
Satoku Matrix Properties
For general matrix cell properties, the standard index scheme for row f and column g is used (f, g ∈ (0,1, ..)) . Rows are denoted by r[f], matrix cells are denoted by c[f,g].
An inverted adjacency matrix is necessarily symmetrical (mirrored at the matrix diagonal). This property follows from mapping an undirected graph to an inverted adjacency matrix. This property also holds for the satoku matrix.
The row and column indexes of a matrix cell are equivalent to the row indexes of the related rows. E.g., cell c[3, 5] refers to row r[3] and row r[5].
If the value of the matrix cell c[f,g] is zero (0), it is said that the selection of row r[f] depends on (conflicts with) the selection of row r[g], or that selection of row r[f] makes selection of row r[g] impossible.
Due to symmetry, it can also be said, that selection of row r[g] depends on (conflicts with) the selection of row r[f].
If the value of the matrix cell c[f,g] is one (1), it is said that the selection of row r[f] is independent from the selection of row r[g].
Due to symmetry, it can also be said, that the selection of row r[g] is independent from the selection of row r[f].
Fun fact (just to see, whether TeX conversion works): Given a set of clauses C and a set of variables V, the matrix cell count MC is:
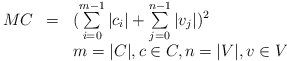
Therefore the space requirements of the mapping algorithm are O(m^2).
Requirements Update Algorithm
The satoku matrix is used as a dynamic data structure. It is therefore necessary to define the operations in a manner as to preserve the properties of an inverted adjacency matrix.
Selection Logic
The logic of selections involves the boolean values 0, 1 and the logical functions AND and (implicitely) X1.
X1 stands for single selection (see DOGgy style programming, section Ternary Logic Functions).
The hard/soft property is determined contextually and has different semantics in regard to the required updates and the relationship between selection rows. However, for the purpose of logical operations both hard ones and soft ones have the boolean value 1.
Since there are no changes from zero to one in the scope of this algorithm, these do not have to be considered (design principle to avoid weak decisions). See section Making Decisions for backtracking provisions.
Mirror Property
Each matrix cell c[f,g] has a mirror cell c[g ,f], which must be kept synchronized. Cells on the matrix diagonal are their own mirror, which makes synchronization trivial since they are obviously always synchronized to themselves. (If you wish, you can also posit that cells on the matrix diagonal do not have a mirror. The effect is the same.)
Lemma: Ask your local computer science professor, which interpretation is least disruptive and then choose the one you like best, depending on your mood, or if you forgot it on the way home. It may be advantageous to take notes, but DOGgy style predicts that you will forget that, too. Or you will not find the notes when you need them. So it may be a waste of energy after all.
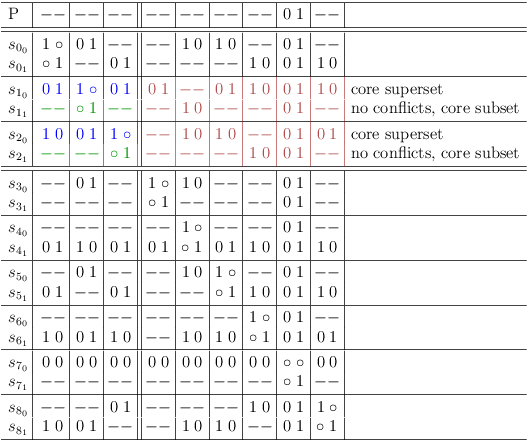
Soft/Hard Property, Superset Rows
If there is a selection row s[i,j], with a hard one in cell c[[i,j] [f,g]], it follows, that if the selection represented by r[f] is made then the selection represented by s[i,j] must also be made. This is necessary to preserve satisfiability.
Therefore, all values in the matrix cells c[[i,j], [x,y]] of selection row s[i,j] are replaced by the logical AND of the value in c[[i,j], [x,y]] and the value in c[[f,g], [x,y]] from selection row s[f,g]:
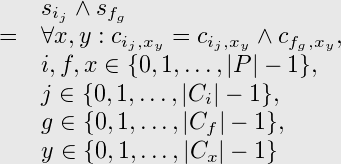
This effectively adds all conflicts (zeroes) from selection row s[f,g] to selection row s[i,j].
It is said, that selection row s[i,j] requires selection row s[f,g] (necessary selection). Therefore, s[i,j] is called a superset row of s[f,g].
RT: O(n)
Lemma: This is a perfectly good DOGgy style example for illustrating the difference between decision making and information gathering. When a selcetion row s[i,j] requires another selection row s[f,g], there is no decision involved. The decision that this should be the case has already been made by a higher entity. And, for what its worth, it is irrevocable. In other words, it is a fact.
The decision at hand is whether you wish to select this particular row s[i,j] or not. DOGgy style asserts, that this decision you must not make, unless it solves your problem.
One could argue, if it is not known, whether the decision has to be made at all, then why bother with following the consequences in case it will ever be made? It would have been a waste of time to follow up, if the final decision was to not select the row.
That is true, but you cannot make an informed decision, if you do not gather the necessary information. For all you know, this decision could lead to the philospher's stone, which would be some nice fodder for your DOG.
But don't get excited and keep your DOG on the leash. Information gathering is a pretty dull process. Do not go on a venture, only collect what is readily available, do not make decisions that may have to be reversed (at great expense) later on and wait for it to settle.
Just remember, that procrastination of decision making is not the same as sloppiness. Delusions of grandeur stare right at you, if you think you can make a decision without information.
If it so happens, that a clause segment cs[[i,j], f] of a selection row s[i,j] is filled with zeroes except for a single soft one at c[[i,j], [f,g]], the soft one is converted to a hard one and the conflicts of the required selection row s[f,g] are added to row s[i,j].
RT: O(n)
If new conflicts are added to a selection row, all superset rows must be updated accordingly (see Worst Case Running Time below) .
Unselectable Rows, Unsatisfiability
If it so happens, that any clause segment cs[[i,j], f] of a selection row s[i,j] is filled entirely with zeroes, it can no longer be selected at all, i.e., it becomes unselectable. Therefore the entire row s[i,j] is filled with zeroes. Due to the mirror cell requirements, column sc[i,j] is also filled with zeroes.
RT: O(n)
If all rows in a clause sub-matrix become unselectable, the corresponding logical problem becomes unsatisfiable.
RT: O(1)
Requirement Update Example
Here is an example to illustrate the requirement update.
Transition 1 -> 0:
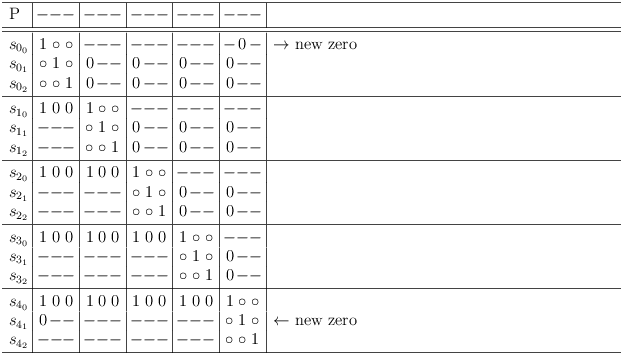
Mark requirement updates:
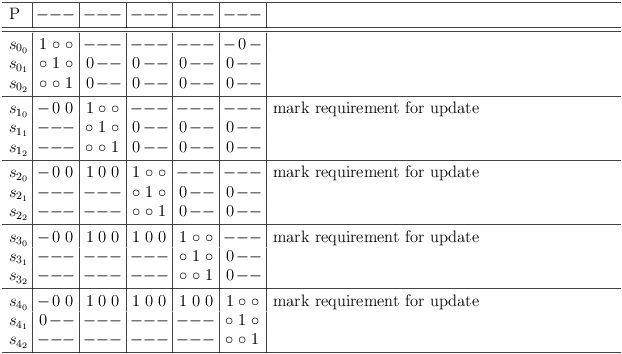
First requirement update leads to 1 -> 0 transition and more requirement updates:

This continues:

until the last requirement update does not cause any changes:
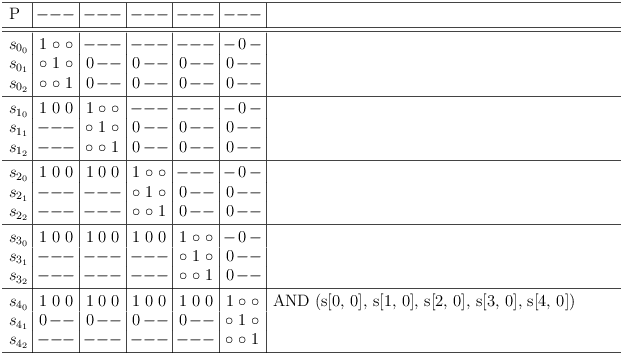
Worst Case Running Time
For a satoku matrix M, a transition 1 -> 0 triggers m requirement updates, m = number of selection rows in M.
The cost for marking the maximum number of requirement updates is m.
Each requirement update involves a maximum of m linear AND operations.
Each requirement update causes a transition 1 -> 0, which in turn causes m further requirement updates.
The maximum cost for marking and applying requirement updates is therefore m * m * m = m^3.
If a selection becomes impossible, m-1 selection rows are affected and therefore m-1 requirement updates are potentially detected.
This process will definitely stop, when all clause sub-matrixes degrade to 1-SAT clauses, making them all identical. The worst case running time is therefore O(P), P = m^x, x = (1, 2, ..).
Summary
The most expensive part of the program is the algorithm to keep the matrix cells up to date.
I am using crude implementations in C++, Perl and Emacs Lisp since olden days. Although I have already designed a more efficient version, I have yet to encounter the urgent need to implement it.
Lemma: In DOGgy style programming it is allowed to give run-time efficiency estimates based on subjective intuitive experience. Maybe brag a little bit about what size problems you were working on? 232 clauses, 87 variables, really? 260 clauses, 391 variables, good. With unoptimized Emacs Lisp? How funny!
The significance of a soft one is, that it can be changed to zero without further adverse consequences, while a hard one cannot be changed to zero without rendering the row unselectable. Therefore, a soft one can also be called a possible selection, while a hard one is called a necessary or required selection.
To make it perfectly clear, here are the only possible state transitions of matrix cell values in the scope of this algorithm:
Other Operations
In the context of this discussion, a satoku matrix is also manipulated in the following ways:
- Selection rows (and corresponding columns) are removed.
- Requirements update algorithm is not necessary if the selection row was already unselectable.
- Requirements update algorithm is necessary after each removal of a selectable row (rows must be removed sequentially).
- Entire clause sub-matrixes (including their vertical counterparts) are removed. There is no action necessary after removal.
- Entire empty clause sub-matrixes (including their vertical counterparts) are added. There is no action necessary after addition.
- Selection row conflicts are added manually. Requirements update algorithm is necessary after any change to a selection row.
Conflict Maximization
It becomes obvious, that zeroes and hard ones are a good thing. Soft ones eventually require a decision to be made, which is known to be prone to inefficienct backtracking.
So, let's extend the original formula a little. The following extension:
is applied to the previous SAT instance:
(¬a ∨ ( a ∧ ¬b) ∨ ( a ∧ b ∧ c)) ∧ (¬a ∨ ( a ∧ b) ∨ ( a ∧ ¬b ∧ ¬c)) ∧ (¬a ∨ ( a ∧ b) ∨ ( a ∧ ¬b ∧ c)) ∧ ( a ∨ (¬a ∧ ¬b) ∨ (¬a ∧ b ∧ ¬c)) ∧ ( a ∨ (¬a ∧ ¬b) ∨ (¬a ∧ b ∧ c)) ∧ ( a ∨ (¬a ∧ b) ∨ (¬a ∧ ¬b ∧ ¬c)) ∧ ( a ∨ (¬a ∧ b) ∨ (¬a ∧ ¬b ∧ c)) ∧ ( a ∨ ¬a) ∧ ( b ∨ ¬b) ∧ ( c ∨ ¬c)
Proof: With:
A = ¬p ∧ q B = ¬p ∧ ¬q ∧ rinduction over the full truth table:
p q r ¬p ¬q A B p ∨ q ∨ r p ∨ A ∨ B 0 0 0 1 1 0 0 0 0 0 0 1 1 1 0 1 1 1 0 1 0 1 0 1 0 1 1 0 1 1 1 0 1 0 1 1 1 0 0 0 1 0 0 1 1 1 0 1 0 1 0 0 1 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 1 1 shows that (p ∨ q ∨ r) and (p ∨ A ∨ B) are logically equivalent.
For the mapping of a SAT problem to a satoku matrix it is necessary to decide, whether a literal and a conjunction can be selected independently or not. This is formalized in the following statements.
A literal l and a conjunctive clause C can be selected independently, if the literal l can be selected independently from all literals l[c] of C:
Proof: is trivial: p ∧ (q ∧ r) = (p ∧ q) ∧ (p ∧ r).
Two conjunctive clauses C0, C1 can be selected independently, if all literals l[i] of C0 can be selected independently from all literals l[j] of C1:
RT: O(k^2), k = |C|
The extended SAT formula is now mapped into the satoku matrix and the requirements update algorithm is applied:
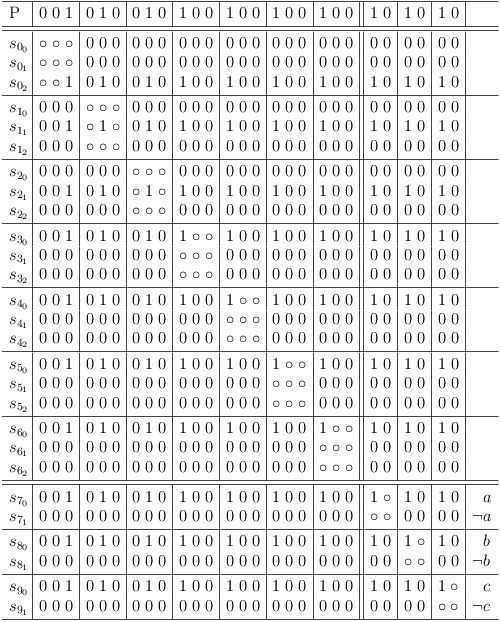
Surprised much? Probably not. The CNF formula was just an encoded conjunction (a ∧ b ∧ c) to begin with. (I chose it for the high density instant solution effect).
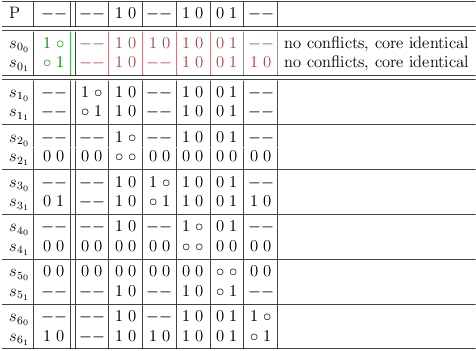
Here are some more properties that can be observed:
- Rows that require each other become identical (this can be used to optimize the requirements update algorithm).
- If a clause has only one selectable row, that row is required by all other clauses (1-SAT property).
- Unselectable rows and their corresponding columns can be removed from the matrix. (Note, that this may break the relation between selection row indexes and clause literal indexes).
- If two clauses consist of only identical rows (each row of one clause requires exactly one row in the other clause) (redundant clauses), one of the clauses (rows and corresponding columns) can be removed from the matrix. (Note, that this will break row/clause index relations).
- A redundant clause can also be removed, if each row of a clause presents the same conflict structure as a row in the other clause (except for the clause segments at the matrix diagonal). (Note, that this also breaks row/clause index relations).
Here is the result, after cleaning up the satoku matrix:
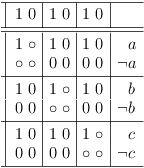
For obvious reasons, the variable selection clauses have been left intact. However, the selection indices have been removed because they do no longer represent the selection row/SAT clause relation correctly.
Lemma: Once a problem is solved, it is good to clean up. Since all disambiguities have been resolved. It is also good to remove information that is no longer applicable!
Merging Clause Sub-Matrixes
Iff a single selection must be made from one clause and a single selection must be made from another clause, then a single selection must be made from the possible combinations of exactly one literal from one clause and exactly one literal from the other clause:
X1(p, q) ∧ X1(r, s) ↔ X1(p ∧ r, p ∧ s, q ∧ r, q ∧ s)
Proof:
Let statements A and B be:
A = X1(p, q) ∧ X1(r, s) B = X1(p ∧ r, p ∧ s, q ∧ r, q ∧ s)Induction over the full truth table shows, that statement A and statement B are logically equivalent:
p q r s X1(p, q) X1(r, s) A p ∧ r p ∧ s q ∧ r q ∧ s B A 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 1 1 1 0 0 0 1 1 1 0 1 1 0 1 1 1 0 0 1 0 1 1 0 1 1 1 1 0 0 0 0 1 1 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 1 1 1 1 0 1 0 0 1 1 1 0 1 0 1 1 1 1 0 0 0 1 1 1 0 1 1 1 0 0 1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 1 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 0 1 0 0 0 1 1 1 1 0 0 0 1 1 1 1 0 0 Note, that p, q, r, s stand for the truth value of a selection being made, they do not refer to any boolean values of variables in the underlying SAT problem. (I hope that is enough).
The problem with this proof is, that n-ary single selection X1 cannot be defined recursively like other logical functions. So it could be argued, that it should be proved for all possible cases of n-ary single selection, which of course is not possible. If anybody has a better idea, please, let me know (combinatorics maybe?).
From what I understand, that principle is somehow related to the DPLL algorithm and possibly does not need to be proved. That would be nice.
Lemma: DOGgy style programming encourages you to prove things to yourself. Choose the method best suited for your purpose and don't worry about other people so much. You can find out later, what the correct way is.
I think I have a better idea! Based on De Morgan's laws and the distributive property, P ∧ (Q ∨ R) = (P ∧ Q) ∨ (P ∧ R), a different proof would be as follows. The equivalence
(p ∨ q) ∧ (r ∨ s) = ((p ∧ r) ∨ (p ∧ s) ∨ (q ∧ r) ∨ (q ∧ s))
allows to transform the conjunction of two disjunctive clauses into a single disjunctive clause with 4 conjunctive sub-clauses. According to the principle of conflict maximization, this constitutes a single clause SAT problem which can be mapped into a single clause satoku matrix.
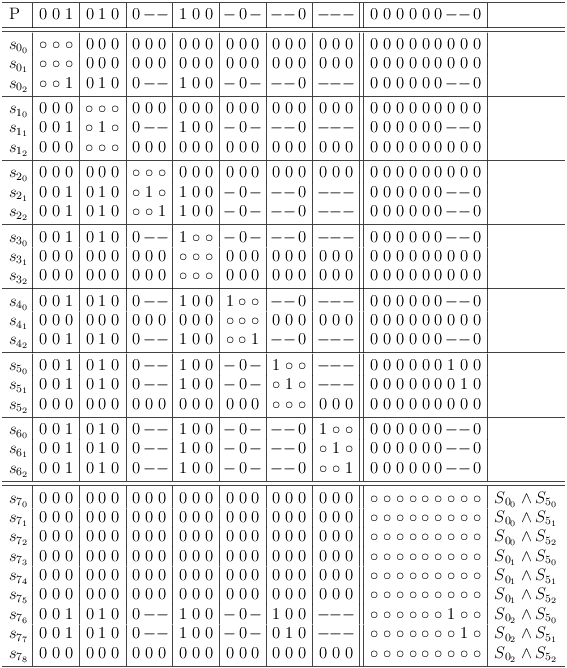
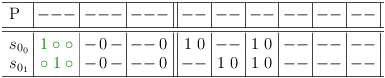
Back on topic, let's start with the example conjunction from above. The goal is to merge clause sub-matrixes S0 and S5.
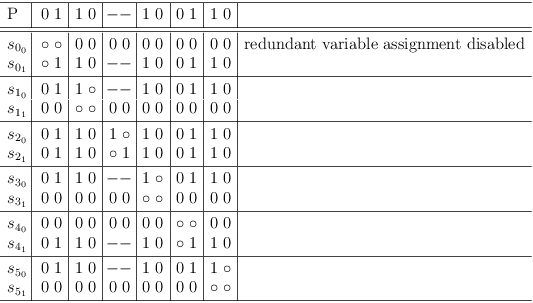
When counting the possible and impossible selections in the clause conflict sub-matrix S[0, 5] at the intersection of row S0 and column S5, the number of possible selections is the predicted number of selection rows, which the merge result will have (in this case: 6).
Both clause sub-matrixes S0 and S5 have 3 selection rows each. The number of possible combinations is therefore 3 * 3 = 9.
Start merging by adding an empty clause sub-matrix with 9 rows and columns (press `C-u 9 > >' in satoku-mode), and fill out clause conflict sub-matrix S[7, 0] with requests for all selection rows of clause sub-matrix S0. Each request must be repeated twice for a total of 3 requests per selection row:

Now clause conflict sub-matrix S[7, 5] is also filled with 3 requests each per selection row of S5. However, the order of the requests must be chosen such as to produce all possible combinations of selection rows:

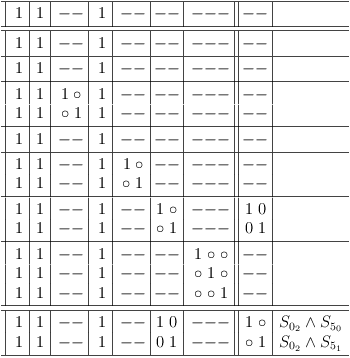
When the requirements update algorithm has finished (press `r u' in satoku-mode), the satoku matrix looks pretty torn up:
After removing the impossible selections (rows/columns with all zeroes) (press `d l' in satoku-mode on a row with all zeroes to delete it[sm-single]), a conflict free satoku matrix is revealed, which still has some single row clauses (aka. 1-SAT clauses) and two identical clause sub-matrixes (they require each other):
The final result, after removing the trivial single row clause sub-matrixes and the redundant clause sub-matrix (press `d L' in satoku-mode to remove a clause sub-matrix):
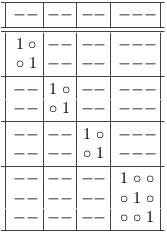
All selection rows can be mapped to truth assignments of the SAT problem variables, since no conflicts (zeroes) are present.
It appears as if there are many solutions to the problem, but when the variables are also mapped, it can be seen, that the truth value assignment for all selection rows is identical. The effective assignment is the single solution for the conjunction (a ∧ b ∧ c):
| [sm-single] | In satoku-mode it is not possible to delete a row, when there are only two rows left. This is a restriction of the clause detection algorithm, which is not very thoroughly designed. (The insight, that rows/columns can be removed came quite late). |
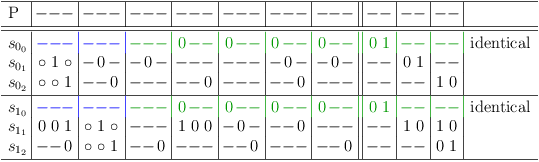
Conflict Comparison
The special clause identity segment cs[[i,j], i] is ignored in each selection row, when comparing the conflicts of selection rows. The difference in the clause identity segments trivially states, that the selection rows represent different selections. But clearly the effects of different selections can still be the same.
E.g., given two selection rows s[0, 0], s[0, 1]:
for the purpose of conflict comparison, the clause identity segments cs[[0, 0], 0] and cs[[0, 1], 0] are assumed to be set to 1:

The comparison shows, that the effect of either selection is identical in the core problem sub-matrix and that the effect is different in the variable section.
Whether selection rows conflict with each other or not is immaterial for conflict comparison. It follows for selection rows in different clauses, that both clause identity segments are ignored in both selection rows.
E.g., given two selection rows s[0, 0], s[1, 0]:
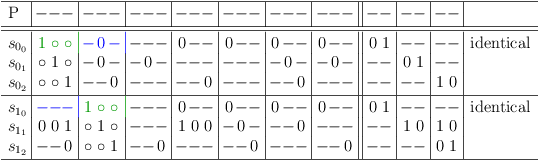
for the purpose of conflict comparison, the clause identity segments cs[[0, 0], 0], cs[[0, 0], 1], cs[[1, 0], 0] and cs[[1, 0], 1] are assumed to be set to 1:
Clause Reduction By Redundancy Removal
- If there are two selection rows in the same clause sub-matrix, where one selection row is a superset of of the other selection row, the superset can be removed (obfuscation).
- From 1. follows: If two selection rows in the same clause sub-matrix present the same conflicts, one of them can be deleted.
Proof:
Given selection s[i,j] and selection s[i, h], a common conflicting selection q, and a conflicting selection r which is unique to selection s[i, h]:
selection s[i,j] -> ¬q selection s[i, h] -> ¬q ∧ ¬r p = selection s[i,j] ∨ selection s[i, h]it follows, that making any of the selections will make selection q impossible or it will make both selections q and r impossible:
p -> ¬q ∨ (¬q ∧ ¬r)Full induction based on the truth table:
p q r ¬r ¬q ¬q ∧ ¬r p -> ¬q ∧ ¬r p -> ¬q p -> ¬q ∨ (¬q ∧ ¬r) 0 0 0 1 1 1 1 1 1 0 0 1 0 1 0 1 1 1 0 1 0 1 0 0 1 1 1 0 1 1 0 0 0 1 1 1 1 0 0 1 1 1 1 1 1 1 0 1 0 1 0 0 1 1 1 1 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 shows that there is no difference in the result if the term (¬q ∧ ¬r) is dropped. Therefore, it is sufficient to consider selection s[i,j] only.
Note: if only the core part of the selection rows is considered, the total number of solutions will be incorrect, if the variable requirements differ. However, satisfiability cannot be affected, since the core problem is sufficient to determine satisfiability. The variable part is entirely optional.
Note: Do not forget to run the requirements update algorithm after removing a selection row, especially if there is a differing variable part and only the core problem part was considered matching. Also run the requirements update algorithm before removing an entire clause.
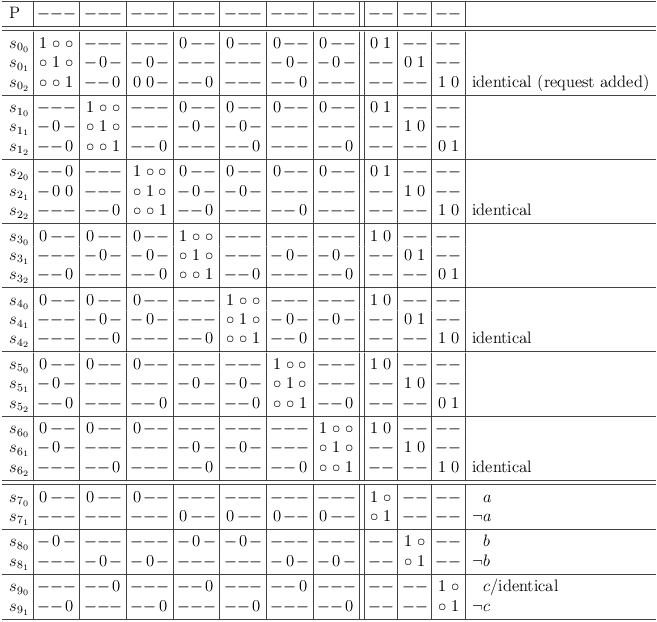
Example:

After first round of redundancy elimination:
Note: If a selection row does not have any conflicts, this corresponds to the statement:
"If a variable appears only unnegated or only negated in a forumula, it can be set to T or F respectively and all clauses containing the literal can be removed from the formula."
After second round of redundancy elimination:
Final result:
Cross Clause Requirements
- If there are two lines in different clause sub-matrixes, where one line is a subset of of the other line, the subset can be made a requirement of the superset, if they do not conflict with each other.
- From 1. follows: If two lines in different clause sub-matrixes present the same conflicts, they can be made identical, if they do not conflict with each other.
Note: requirement requests must be issued sequentially. I.e., after a request, the requirements update algorithm must be run, before the next request can be issued.
The following example shows how a requirement request is added to the clause segment cs[[0, 2], 2] of selection row s[0, 2]:
That request is enough to let the requirements update algorithm detect the underlying conjunction:
Alternate Clause Representations
If several lines in different clause sub-matrixes present the same conflicts, but cannot be made identical, they represent a single selection of lines distributed across clause sub-matrixes. They can be placed into a clause sub-matrix of their own. An additional line is added to allow for none of the lines to be selected. (See Strange Thing for an alternate approach to that type of conflict).
The regular clause sub-matrixes are implictely based on such a construct. In this example the selection rows s[2, 0], s[3, 0], s[4, 0] are mutually exclusive:
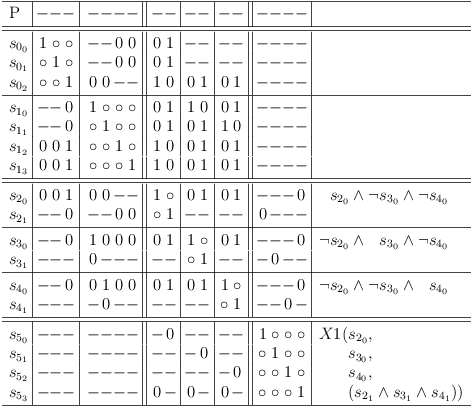
The requirements update algorithm normalizes this as shown in the following satoku matrix. Note, that the alternative "none selected" is invalid:
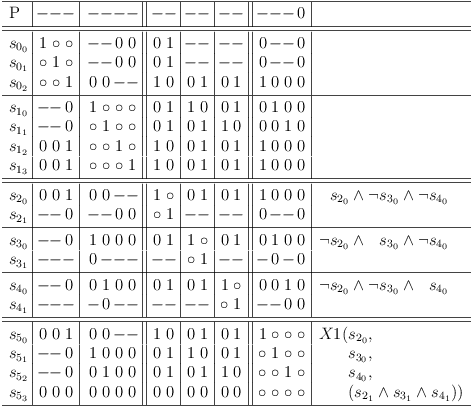
Reverse Mapping of a Satoku Matrix
Based on the equivalence:
p → q = ¬p ∨ q
If a selection s[i,j] is made, it follows that another selection s[k, l] cannot be made.
E.g., encoding this satoku matrix:
// | || S|| 0| 0|| 1 1 1 | 1 1 1 | // +----++----++---+----++-------+-------+ // +-----+----++---+----++-------+-------+ // | | 0|| | || 1 * * | 0 _ _ | // | | 1|| | || * 1 * | _ 0 _ | // | | 2|| | || * * 1 | _ _ 0 | // +-----+----++---+----++-------+-------+ // | | 3|| | || 0 _ _ | 1 * * | // | | 4|| | || _ 0 _ | * 1 * | // | | 5|| | || _ _ 0 | * * 1 | // +-----+----++---+----++-------+-------+ // |:info:| move point inside and press `C-u M-x satoku-mode RET'
renders (redundant clauses removed):
// S0 weak selection (allow one or more selections) s[0,0] ∨ s[0,1] ∨ s[0,2] // S0 intra-clause conflicts (require single selection) ¬s[0,0] ∨ ¬s[0,1] ¬s[0,0] ∨ ¬s[0,2] ¬s[0,1] ∨ ¬s[0,2] // S1 weak selection (allow one or more selections) s[1,0] ∨ s[1,1] ∨ s[1,2] // S1 intra-clause conflicts (require single selection) ¬s[1,0] ∨ ¬s[1,1] ¬s[1,0] ∨ ¬s[1,2] ¬s[1,1] ∨ ¬s[1,2] // S[0, 1] inter-clause conflicts ¬s[0,0] ∨ ¬s[1,0] ¬s[0,1] ∨ ¬s[1,1] ¬s[0,2] ∨ ¬s[1,2]
In order to produce a SAT problem with CNF clauses, the disjunctions (OR) are mapped to a set of disjunctive clause vectors.
Since the SAT problem to satoku matrix mapping function explicitely adds the intra-clause conflicts, they can be dropped in the reverse mapping:
[ 1 1 1 - - - ] [ - - - 1 1 1 ] [ 0 - - 0 - - ] [ - 0 - - 0 - ] [ - - 0 - - 0 ] s s s s s s 0 0 0 1 1 1 0 1 2 0 1 2
The clause vectors can then be translated to a SAT problem in conjunctive normal form[15]:
( s00 ∨ s01 ∨ s02) ∧ ( s10 ∨ s11 ∨ s12) ∧ (¬s00 ∨ ¬s10 ) ∧ (¬s01 ∨ ¬s11 ) ∧ (¬s02 ∨ ¬s12 )
If you map this problem back to a satoku matrix (without mapping the variables!), this is what you get:
// | || S || 0| 0|| 1 1 1 | 1 1 1 || 1 1 | 1 1 | 1 1 | // +-----++---++---+----++-------+-------++-----+-----+-----+ // +-----+----++---+----++-------+-------++-----+-----+-----+ // | 0 H| 0|| 2| 2|| 1 * * | 0 _ _ || _ _ | _ _ | 1 0 | // | | 1|| 2| 2|| * 1 * | _ 0 _ || _ _ | 1 0 | _ _ | // | | 2|| 2| 2|| * * 1 | _ _ 0 || 1 0 | _ _ | _ _ | // +-----+----++---+----++-------+-------++-----+-----+-----+ // | 1 H| 3|| 2| 2|| 0 _ _ | 1 * * || _ _ | _ _ | 0 1 | // | | 4|| 2| 2|| _ 0 _ | * 1 * || _ _ | 0 1 | _ _ | // | | 5|| 2| 2|| _ _ 0 | * * 1 || 0 1 | _ _ | _ _ | // +-----+----++---+----++-------+-------++-----+-----+-----+ // +-----+----++---+----++-------+-------++-----+-----+-----+ // | 2 H| 6|| 1| 1|| _ _ _ | _ _ 0 || 1 * | _ _ | _ _ | // | | 7|| 1| 1|| _ _ 0 | _ _ _ || * 1 | _ _ | _ _ | // +-----+----++---+----++-------+-------++-----+-----+-----+ // | 3 H| 8|| 1| 1|| _ _ _ | _ 0 _ || _ _ | 1 * | _ _ | // | | 9|| 1| 1|| _ 0 _ | _ _ _ || _ _ | * 1 | _ _ | // +-----+----++---+----++-------+-------++-----+-----+-----+ // | 4 H| 10|| 1| 1|| _ _ _ | 0 _ _ || _ _ | _ _ | 1 * | // | | 11|| 1| 1|| 0 _ _ | _ _ _ || _ _ | _ _ | * 1 | // +-----+----++---+----++-------+-------++-----+-----+-----+
Interesting, isn't it? Obviously each 2-literal clause vector maps nicely to a variable.
So the satoku matrix can also be mapped to a SAT problem in this manner:
with s[2,0] = a, s[2,1] = !a, s[3,0] = b, s[3,1] = !b, s[4,0] = c, s[4,1] = !c: (a | b | c ) & (!a | !b | !c)
This shows unambiguously, that in the context of the satoku matrix it is completely irrelevant to make any distinction between variables and 2-SAT clauses. Their effects are identical.
1,2,k-SAT, soft, hard, weak and strong
Now, that we have come full circle mapping SAT problems to satoku matrixes and satoku matrixes back to (possibly different, but isomorphic) SAT problems, it is a good time to consolidate the theory.
In the context of satoku matrixes (and CNF formulas for that matter), there is nothing special about 1-SAT, 2-SAT, k-SAT with k >=3. The only difference is the effect of conflicts. But the conditions remain the same:
- If a clause segment in a selection row has no possible selections (ones), the entire selection row becomes impossible and the selection row and corresponding column are filled with zeroes.
- If all selection rows of a clause sub-matrix become impossible, the entire problem is unsatisfiable. (My crude version of the requirements update algorithm actually follows the propagation rules and fills the entire satoku matrix with zeroes for no deeper purpose at all.)
1-SAT Problems
For clauses of 1-SAT problems, that means, that case 1 and 2 are identical. Both happen, as soon as a single conflict is introduced. I.e. for a 1-SAT problem to be satisfiable, there must not be any concflicts. It follows, that all ones are hard ones and no weak decisions can be made.
Unless you are completely stoned or remarkably stubborn. Actually, if the problem is satisfiable, you can only make a single very strong decision, which is that you can just deny it anyway.
2-SAT Problems
With 2-SAT problems, there can be at most one conflict in any clause segment of a selection row. A conflict in a 2-SAT clause segment is immediately propagated throughout the entire satoku matrix by the requirements update algorithm. Soft ones only appear completely unrestricted, i.e., they cannot be combined with a conflict and still remain soft ones.
When a selection row becomes impossible, a 2-SAT clause sub-matrix degrades to a 1-SAT clause sub-matrix.
It follows, that the effects of a conflict in a 2-SAT problem are immediately known. There are no conflicts, that can be detected "later". Making Weak decisions based on soft ones remains possible. But since there is no need, it seems pretty clumsy. And the propagation of the consequences will immediately show, whether it was a good or bad decision.
The following example demonstrates that it is impossible to construct an indirect contradiction in a 2-SAT satoku matrix.
For an indirect contradiction, we need 2 selection rows s[0, 0], s[1, 0] that result in a contradiction (s[2, 0] cannot be selected) when both are actually selected:
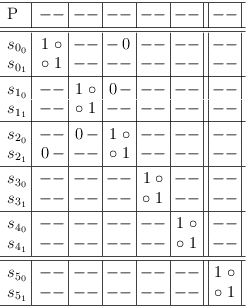
Add two more selections s[3, 0], s[4, 0], which - when actually selected together - will require both s[0, 0] and s[1, 0]:
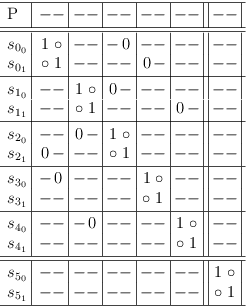
Selection row s[5, 0] requires both s[3, 0] and s[4, 0], which will indirectly lead to a contradiction:
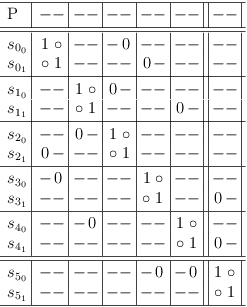
The resulting satoku matrix looks perfectly fine, as long as the consequences of conflicts are ignored. But, running the requirements update algorithm detects the contradiction immediately:
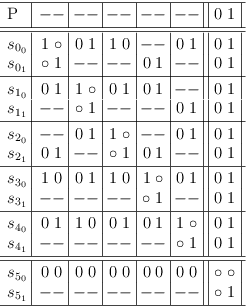
This example also shows, that mapping a SAT problem to an inverted adjacency matrix and ignoring the clause constraints as negligible (since they are implicit) is a fallacy. It further shows, that mapping a 2-SAT problem to a DFS (depth-first search) graph is clumsy, since the representation of all possible solutions is unstructured and an additional search operation is needed to determine satisfiability.
Note
It may be interesting to check, whether mapping the DFS graph to an inverted adjacency matrix is equivalent to mapping the 2-SAT problem directly. But anyhow, the required DFS is definitely not equivalent to the requirements update algorithm.
Extracting Solutions from 2-SAT Satoku Matrixes
The set of unique solutions for a 2-SAT problem can be determined in the following manner.
The following 2-SAT problem:
( ¬p ∨ ¬r ) ∧ ( ¬p ∨ s ) ∧ ( ¬p ∨ t ) ∧ ( ¬p ∨ ¬u ) ∧ ( p ∨ q ) ∧ ( q ∨ ¬r ) ∧ ( q ∨ s ) ∧ ( q ∨ t ) ∧ ( q ∨ ¬u ) ∧ ( r ∨ s ) ∧ ( r ∨ t ) ∧ ( r ∨ ¬u ) ∧ ( ¬s ∨ t ) ∧ ( ¬s ∨ ¬u ) ∧ ( t ∨ u )
maps to:
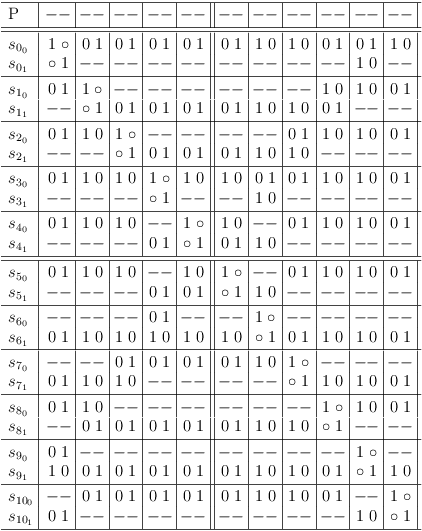
After removing redundant clauses, find a variable selection row with the maximum number of conflicts:
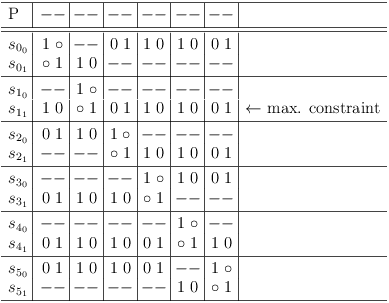
Use the (possibly partial) selection row as solution, disable the selection and continue with the next selection row, that has the maximum number of conflicts:
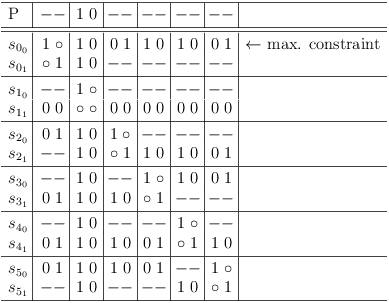
Repeat, until all solutions are extracted:
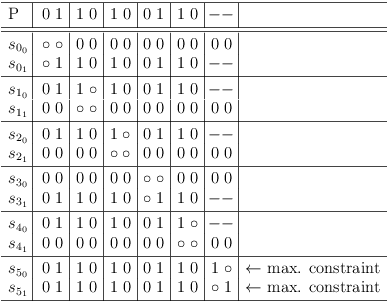
The set of solutions for this problem is:
[ 1 0 0 1 1 0 ] [ 1 1 0 1 1 0 ] [ 0 1 0 1 1 0 ] [ 0 1 1 1 1 0 ] [ 0 1 1 0 0 1 ] [ 0 1 1 0 1 1 ] [ 0 1 1 0 1 0 ] p q r s t u
This algorithm also works trivially for solution sets without conflicts:
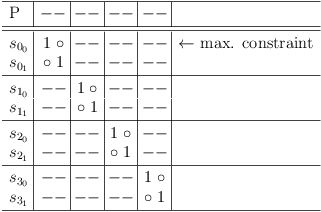
The next partial solution:

The entire set of partial solutions is:
[ 1 _ _ _ ] // 2^3 = 8
[ 0 1 _ _ ] // + 2^2 = 4
[ 0 0 1 _ ] // + 2^1 = 2
[ 0 0 0 1 ] // + 1
[ 0 0 0 0 ] // + 1
a b c d // ----------
// 16
3-SAT Problems
Only k-SAT, k>=3 eventually requires weak decisions, because conflicts from two different clauses can combine during a merge operation in such a manner, that a soft one must be converted to a hard one. Since the effects of the newly detected hard one only become known, when the merge actually happens, such k-SAT problems can become unsatisfiable "later".
When a selection row becomes impossible, a 3-SAT clause sub-matrix degrades to a 2-SAT clause sub-matrix.
Indirect Impossible Selections
An indirect impossible selection occurs, when the selection of two rows eventually requires selecting a third row, which renders the entire selection invalid.
Given the following situation:
Q | * * 1 | .. | 0 - - |
..
R | 0 - - | ..
..
S | - 0 - | .. | - - 0 |
..
T | - - 0 | .. | * 1 * |
when row R and row S are selected together, the selection of row Q is also required:
=> R&S | 0 0 1 | .. | - - 0 | -> requires Q
adding the conflicts from selection row Q leads to the required selection of row T:
=> R&S&Q | 0 0 1 | .. | 0 - 0 | -> requires T
adding the conflicts from selection row T makes the entire selection impossible:
=> R&S&T&Q | 0 0 0 | ..
It is evident, that such a conflict situation requires SAT clauses with a minimum of 3 literals.
Worst Case Upper Bounds
The fact, that 2-SAT problems are immediately solvable means, that k-SAT problems can be solved by making weak decisions that reduce the satoku matrix to a set of 2-SAT problems.
The standard complexity calculations are based on weak decisions over the number of variables n that appear in a SAT problem (1-SAT decisions). I will call this complexity n-complexity (NC) to distinguish it from the complexity calculations based on the number of clauses m, which I will call m-complexity (MC).
For a SAT problem P, with clauses C, it follows, that the upper bound for the worst case running time for clause based decisions is not
k^m, k = |C|, m = |P|,
but
⌈ k/2 ⌉ ^ m
which for 3-SAT and 4-SAT is 2^m.
While m-complexity for a 1-SAT and 2-SAT problems is trivially 1^m = 1, n-complexity for 1-SAT and 2-SAT problems is counter-intuitively still 2^n. This is factually not the case, and therefore a difference must be postulated for 1,2,3-SAT, when using n-complexity.
Summary
Since any "well-formed" x-SAT, x >= 1 eventually degrades to a mixed SAT problem, the distinction between 1,2,3-SAT is essentially meaningless.
The notable special feature of 2-SAT problems is, that they produce a satoku matrix, that is either unsatisfiable or it must have at least one solution, after the initial run of the requirements update algorithm. This follows from the fact, that there cannot be any indirect impossible selections in 2-SAT problems.
So for 2-SAT problems to make the true statement that the problem is satisfiable, it is not even necessary to assign any variables at all.
However, depending on the requirements for acceptable solutions, it may become necessary to arbitrarily reduce a satoku matrix to a 1-SAT problem, if all variables must be assigned.
Making Decisions
While it is possible to make variable based decisions in a satoku matrix, that type of algorithm is already thoroughly researched.
Therefore, this discussion only explores clause based strategies to reduce a k-SAT problem to one or more 2-SAT problems.
|:todo:| 2-SAT backtracking: find the right words ...
There are no provisions for backtracking in the scope of the satoku matrix. The following method can be employed to make it possible:
- Make a copy of the satoku matrix to get 2 sub-problems SM0 and SM1.
- In SM0 enforce the 2-SAT decision.
- In SM1 enforce the complement of the 2-SAT decision (which does not necessarily result in a 2-SAT clause sub-matrix, depending on the size of the original clause sub-matrix).
.
Ci
/\
2 / \ k-2
/ \
Ci,0 Ci,1
/\
2 / \ k -4
/ \
Similarities between MC and NC
Starting with the satoku matrix SM:
- Make a 2 copies of SM and name them SM0, SM1.
- Make selection s[0, 0] impossible in SM0.
- Make the complementary selections s[0, 1], s[0, 2] impossible in SM1.
SM:
// | || S|| 0| 0|| 1 1 1 | 1 1 1 || 1 1 | 1 1 | 1 1 |
// +----++----++---+----++-------+-------++-----+-----+-----+
// +-----+----++---+----++-------+-------++-----+-----+-----+
// | 0 H| 0|| | || 1 * * | 0 _ _ || 1 0 | _ _ | _ _ |
// | | 1|| | || * 1 * | 1 0 0 || 0 1 | 1 0 | 1 0 |
// | | 2|| | || * * 1 | 1 0 0 || 0 1 | 0 1 | 0 1 |
// +-----+----++---+----++-------+-------++-----+-----+-----+
// | 1 H| 3|| | || 0 _ _ | 1 * * || 0 1 | _ _ | _ _ |
// | | 4|| | || 1 0 0 | * 1 * || 1 0 | 0 1 | _ _ |
// | | 5|| | || 1 0 0 | * * 1 || 1 0 | 1 0 | 0 1 |
// +-----+----++---+----++-------+-------++-----+-----+-----+
// +-----+----++---+----++-------+-------++-----+-----+-----+
// | 2 H| 6|| | || 1 0 0 | 0 _ _ || 1 * | _ _ | _ _ | \hphantom{\neg} a
// | | 7|| | || 0 _ _ | 1 0 0 || * 1 | _ _ | _ _ | \neg a
// +-----+----++---+----++-------+-------++-----+-----+-----+
// | 3 H| 8|| | || _ _ 0 | _ 0 _ || _ _ | 1 * | _ _ | \hphantom{\neg} b
// | | 9|| | || _ 0 _ | _ _ 0 || _ _ | * 1 | _ _ | \neg b
// +-----+----++---+----++-------+-------++-----+-----+-----+
// | 4 H| 10|| | || _ _ 0 | _ _ 0 || _ _ | _ _ | 1 * | \hphantom{\neg} c
// | | 11|| | || _ 0 _ | _ _ _ || _ _ | _ _ | * 1 | \neg c
// +-----+----++---+----++-------+-------++-----+-----+-----+
// |:info:| move point inside and press `C-u M-x satoku-mode RET'
SM0:
// | || S|| 0| 0|| 0 1 1 | 1 0 0 || 0 1 | 1 1 | 1 1 |
// +----++----++---+----++-------+-------++-----+-----+-----+
// +-----+----++---+----++-------+-------++-----+-----+-----+
// | 0 H| 0|| | || 1 * * | 0 0 0 || 0 0 | 0 0 | 0 0 |
// | | 1|| | || * 1 * | 1 0 0 || 0 1 | 1 0 | 1 0 |
// | | 2|| | || * * 1 | 1 0 0 || 0 1 | 0 1 | 0 1 |
// +-----+----++---+----++-------+-------++-----+-----+-----+
// | 1 H| 3|| | || 0 _ _ | 1 * * || 0 1 | _ _ | _ _ |
// | | 4|| | || 0 0 0 | * 1 * || 0 0 | 0 0 | 0 0 |
// | | 5|| | || 0 0 0 | * * 1 || 0 0 | 0 0 | 0 0 |
// +-----+----++---+----++-------+-------++-----+-----+-----+
// +-----+----++---+----++-------+-------++-----+-----+-----+
// | 2 H| 6|| | || 0 0 0 | 0 0 0 || 1 * | 0 0 | 0 0 | \hphantom{\neg} a
// | | 7|| | || 0 _ _ | 1 0 0 || * 1 | _ _ | _ _ | \neg a
// +-----+----++---+----++-------+-------++-----+-----+-----+
// | 3 H| 8|| | || 0 1 0 | 1 0 0 || 0 1 | 1 * | 1 0 | \hphantom{\neg} b
// | | 9|| | || 0 0 1 | 1 0 0 || 0 1 | * 1 | 0 1 | \neg b
// +-----+----++---+----++-------+-------++-----+-----+-----+
// | 4 H| 10|| | || 0 1 0 | 1 0 0 || 0 1 | 1 0 | 1 * | \hphantom{\neg} c
// | | 11|| | || 0 0 1 | 1 0 0 || 0 1 | 0 1 | * 1 | \neg c
// +-----+----++---+----++-------+-------++-----+-----+-----+
// |:info:| move point inside and press `C-u M-x satoku-mode RET'
SM1:
// | || S|| 0| 0|| 1 0 0 | 0 1 1 || 1 0 | 1 1 | 1 1 |
// +----++----++---+----++-------+-------++-----+-----+-----+
// +-----+----++---+----++-------+-------++-----+-----+-----+
// | 0 H| 0|| | || 1 * * | 0 _ _ || 1 0 | _ _ | _ _ |
// | | 1|| | || * 1 * | 0 0 0 || 0 0 | 0 0 | 0 0 |
// | | 2|| | || * * 1 | 0 0 0 || 0 0 | 0 0 | 0 0 |
// +-----+----++---+----++-------+-------++-----+-----+-----+
// | 1 H| 3|| | || 0 0 0 | 1 * * || 0 0 | 0 0 | 0 0 |
// | | 4|| | || 1 0 0 | * 1 * || 1 0 | 0 1 | _ _ |
// | | 5|| | || 1 0 0 | * * 1 || 1 0 | 1 0 | 0 1 |
// +-----+----++---+----++-------+-------++-----+-----+-----+
// +-----+----++---+----++-------+-------++-----+-----+-----+
// | 2 H| 6|| | || 1 0 0 | 0 _ _ || 1 * | _ _ | _ _ | \hphantom{\neg} a
// | | 7|| | || 0 0 0 | 0 0 0 || * 1 | 0 0 | 0 0 | \neg a
// +-----+----++---+----++-------+-------++-----+-----+-----+
// | 3 H| 8|| | || 1 0 0 | 0 0 1 || 1 0 | 1 * | 0 1 | \hphantom{\neg} b
// | | 9|| | || 1 0 0 | 0 1 0 || 1 0 | * 1 | _ _ | \neg b
// +-----+----++---+----++-------+-------++-----+-----+-----+
// | 4 H| 10|| | || 1 0 0 | 0 1 0 || 1 0 | 0 1 | 1 * | \hphantom{\neg} c
// | | 11|| | || 1 0 0 | 0 _ _ || 1 0 | _ _ | * 1 | \neg c
// +-----+----++---+----++-------+-------++-----+-----+-----+
// |:info:| move point inside and press `C-u M-x satoku-mode RET'
In this case, making the 2-SAT decision in clause sub-matrix S0 is equivalent to making the 1-SAT decision for variable a (S2).
The MC reduction requirements are fulfilled in both cases, however, not all variables are fully assigned yet. I.e., some arbitrary variable decisions have to be made to produce a full assignment of the variables.
|:todo:| counter examples ... but not the large ones.
Logical Reasoning
It is perfectly possible to use the satoku matrix without programmatically mapping an initial SAT formula.
Let's start with an empty satoku matrix. It is a sea of endless possibilities, since the selection rows in the clause sub-matrixes are not affected by the variables:
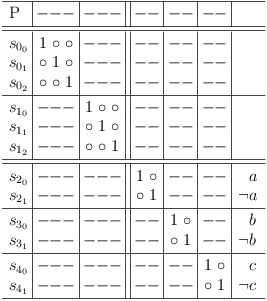
Since each selection row corresponds to the selection of a literal from a SAT problem clause, the first step is to map a clause, e.g., (¬a, ¬b, c) into the satoku matrix. This is real simple, since there are no other dependencies yet:
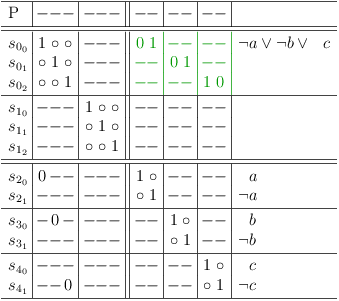
If you are using satoku-mode, the task becomes a lot simpler, because the requirements update algorithm can do most of the work. Since the algorithm looks for the required transition of a soft one to a hard one, a required selection is determined indirectly, by marking all other selections as impossible (this is called filling in a selection request). So let's map the clause (a, b, ¬c):
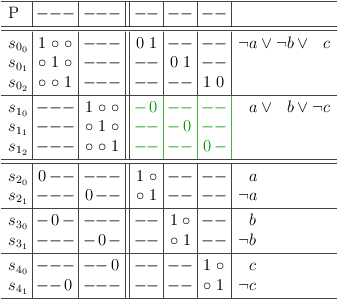
In satoku-mode press `r u' to run the requirements update algorithm. When it has finished, all impossible selections (selection conflicts) for each selection row are properly indicated:
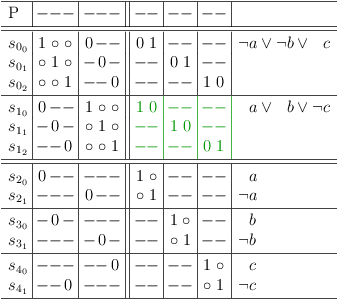
Let's check what happens, when a request is prepared to make selection row s[0, 0] a superset row of selection row s[3, 1], by setting the matrix cell at (s[0, 0], s[3, 0]) to zero. This is logically equivalent to the statement (¬a ∧ ¬b):
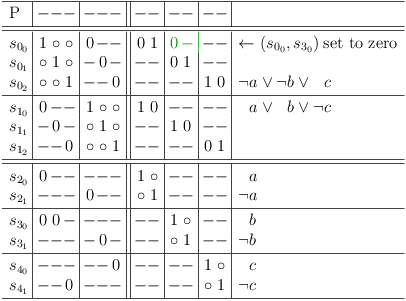
Run requirements update algorithm (press `r u' in satoku-mode) to obtain the final result:

Conflict Maximization Revisited
Conflict maximization was not discoverd the way it is presented, instead it was found by reasoning in a satoku matrix. The figure below shows how (in a partial satoku matrix). (And the description shows, why a logical proof is much clearer than a proof using the satoku matrix).
The SAT clause mapping of (a, b, ¬c) in variable column range
is copied into the variable column ranges
to show the progression of the reasoning. The ranges have been separated from each other by double rules for better visual distinction.
The initial argument concentrates on the region (Ri[0,0], Ri[1,3]), i ∈ (0, 1, .., 4). Row and column indices of ranges Ri[row, column] are relative to the range origin.
In Range R0, the regions (R0[0,2], R0[0,3]) and (R0[1,0], R0[1,1]) contain soft ones, i.e. possible selections.
Ranges R1, R2 show all possible required selections (hard ones) for the region (R0[0,2], R0[0,3]).
Ranges R3, R4 show all possible required selections (hard ones) for the region (R0[1,0], R0[1,1]).
Note, that the effective truth value assignments in ranges R2 and R3 are equivalent. It is therefore allowed to restrict the unrestricted selections of range R0 to the settings of either R1 or R4 without affecting the set of solutions of the corresponding SAT Problem.
By analogy, all possible assignments of range R0 have been prepared for restriction in range R5. Range R6 shows the actual restrictions after running the requirements update algorithm.

It is really important to verify conclusions from logical reasoning in a satoku matrix (as it is for any conclusions :)).
While this looks similar to conflict maximization:
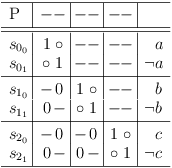
it really is not, since the mirror property demands, that it be corrected to:
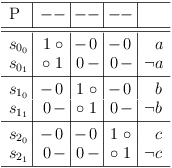
However, this is logically not equivalent to the original satoku matrix.
Conflict maximization can therefore only be applied within a clause conflict sub-matrix, not between clause conflict sub-matrixes.
Extending the original clauses shows what happens logically, when extending variable clauses:
(a ∨ ¬a) ∧ (b ∨ ¬b) ∧ (c ∨ ¬c) = (a ∨ (¬a ∧ ¬a)) ∧ (b ∨ (¬b ∧ ¬b)) ∧ (c ∨ (¬c ∧ ¬c)) (a ∨ (¬a ∧ ¬a)) = (a ∨ ¬a)
The conflicts of tautological variable clauses are already maximized. This agrees with the fact, that single selection is an operation which maximizes the direct conflicts between selections. It is not possible to add any more conflicts without making selections impossible. That is just another way to look at the clause identity sub-matrix.
Clause Construction
Here is a method to construct arbitrary disjunctive clauses from the given variable clause sub-matrixes which was inspired by the reasoning for conflict maximization:
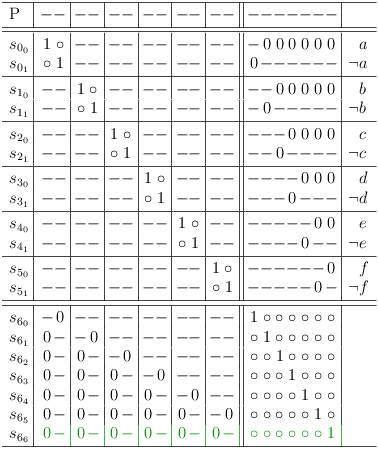
Note the extra line at the bottom, which makes it a tautology. As proved above (proof for adding tautologies), tautologies can be added to a SAT problem without affecting the set of solutions.
The satoku matrix is completed with the requirements update algorithm:
Without any conflicts over the variables, this is not so interesting, but I found, that if the disjunctive requests over all variables are filled out and resolved subsequentially per column (not all at once), it provides a good intuitive estimate for the hardness of a SAT problem.
It will eventually lead to a situation, where no further columns can be added. Considering the number of variables after which that happens is a good indicator, whether the conflict situation is dense or flexible. E.g., XOR-SAT problems are very flexible and you can go very long without running into impossible selections.
Note
Doing this is equivalent to the brute force method of arbitrarily assigning truth values to variables.
|:todo:| prepare example
XOR Structure
Unobfuscated XOR-SAT problems encoded as 3-SAT can be easily detected and the necessary information for generating a system of linear equations can be directly extracted.
XOR encoded as 3-SAT:
(¬a ∨ ¬b ∨ c) ∧ (¬a ∨ b ∨ ¬c) ∧ ( a ∨ ¬b ∨ ¬c) ∧ ( a ∨ b ∨ c)
Observe redundant clause sub-matrixes S0, S1 and S2, S3.
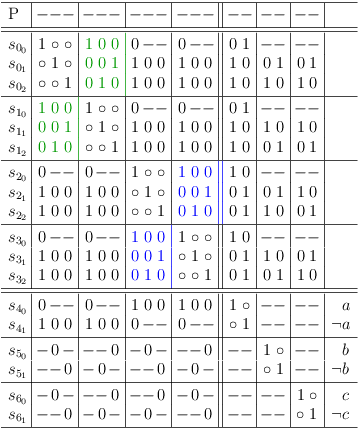
Redundant clause sub-matrixes removed:
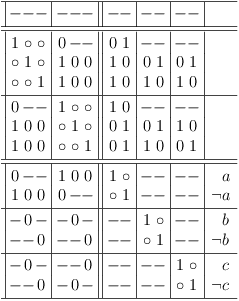
Clause sub-matrixes S0, S1 can be merged into a 4-SAT clause sub-matrix:
s[0, 0] ∧ s[1, 1], s[0, 0] ∧ s[1, 2], s[1, 0] ∧ s[0, 1], s[1, 0] ∧ s[0, 2]
Start by adding a 9-SAT clause sub-matrix, fill the first clause conflict sub-matrix with 3 requests per selection row (3 * 3 = 9), run requirements update algorithm:
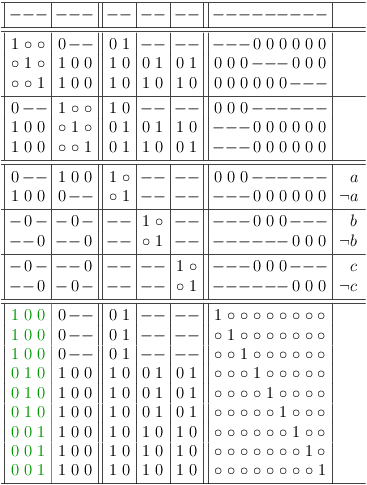
Add a different row request for a row from the second clause sub-matrix for each row request in the first clause sub-matrix. Don't worry, if the request cell is already set to zero, just dont blank out the zero:
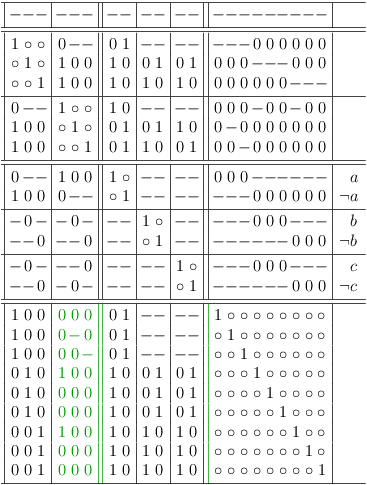
Remove all unselectable rows:
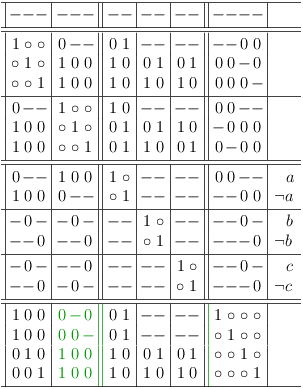
Run requirements update algorithm:
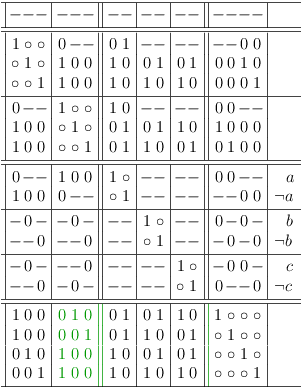
Remove original merge clause sub-matrixes, since they are no longer necessary:
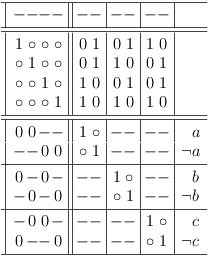
The variable section of clause sub-matrix S0 shows the 4 possible solutions, and how an XOR can be extracted for a linear equation:
The clause section of the variables shows the typical XOR structure.
|:todo:| more images, explain
Bigger XOR-SAT problems necessarily show the same properties.
- initial redundant clause reduction m: -> m/2
- 3/3 -> 4 merge: m -> m/2
Which leaves a 4-SAT problem with 1/4 of the clauses of the original 3-SAT problem.
Since clause-based worst case for 3-SAT and 4-SAT is the same (2^m) this is a complexity reduction from 2^m to 2^(m/4)
Interleaved XOR reduces the problem by 2 clauses per decision, so effective complexity is 2^(m/8)
E.g. mod2-3cage-unsat-9-10, 232 3-SAT clauses, 87 variables:
DPLL-Like Resolution
Note: This algorithm is unresearched (it is based on my naive idea, how DPLL works). It is only listed for completeness.
If there is a conflict beteeen two clauses, it follows, that no matter which of the alternatives is selected, one of the remaining 4 selection rows must also be selected:
X1(p, l1, l2) ∧ X1(¬p, l3, l4) → X1(l1, l2, l3, l4)
Clause sub-matrix S10 is set up for the conflict in cell (s[0, 0], s[5, 0]). It consists of selection rows s[0, 1], s[0, 2], s[5, 1], s[5, 2]:
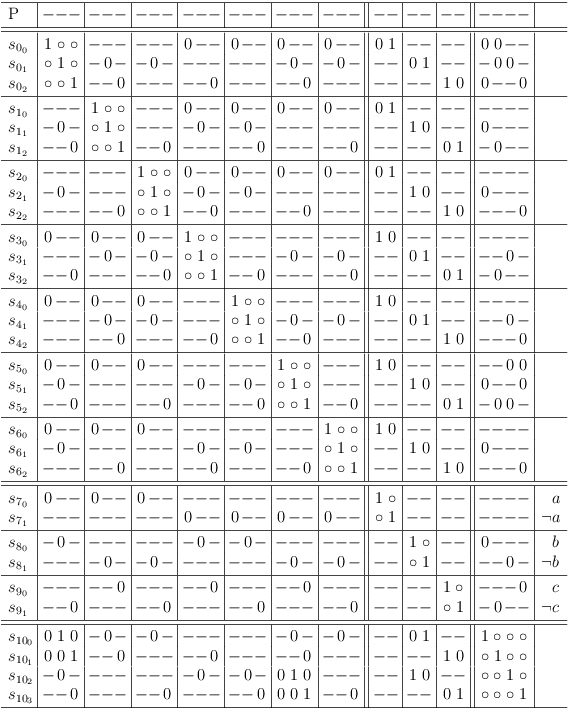
Even, if all conflicts are resolved (clause sub-matrixes S10, S11, S12), it does not help much. It is also possible that redundant selection rows appear in the resolution clause sub-matrix, see S13 and reordered copy S14:
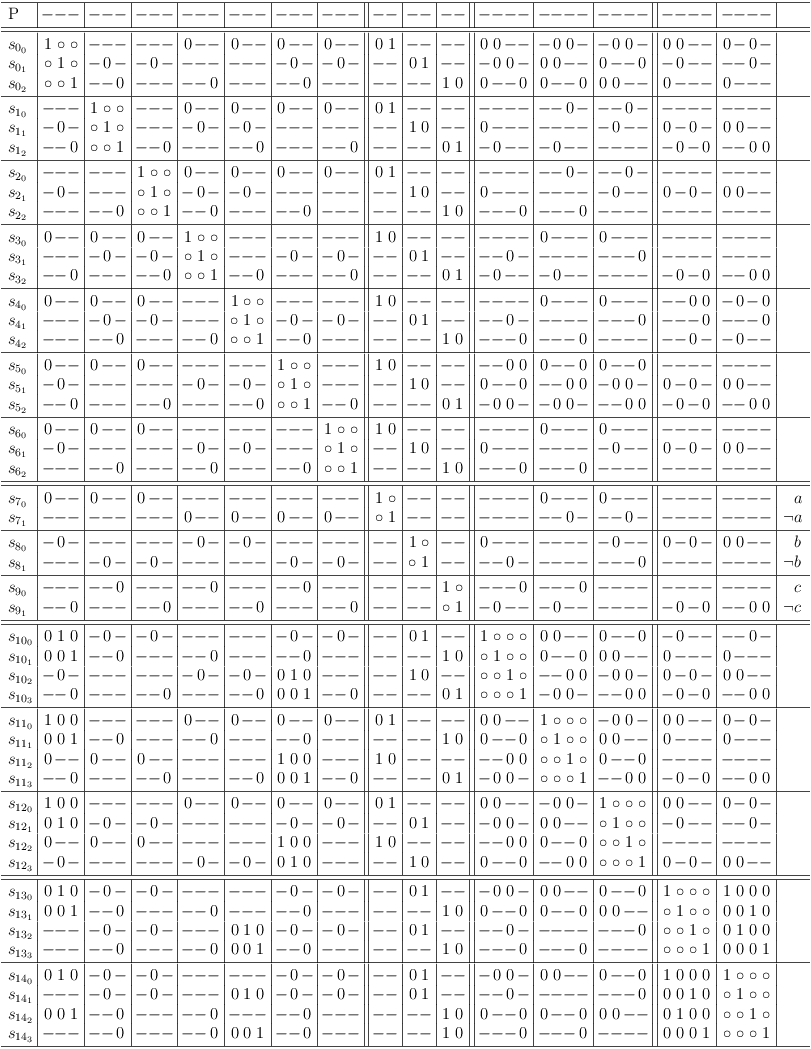
When the common parts (S11) of the redundant selection rows (S12) are extracted,
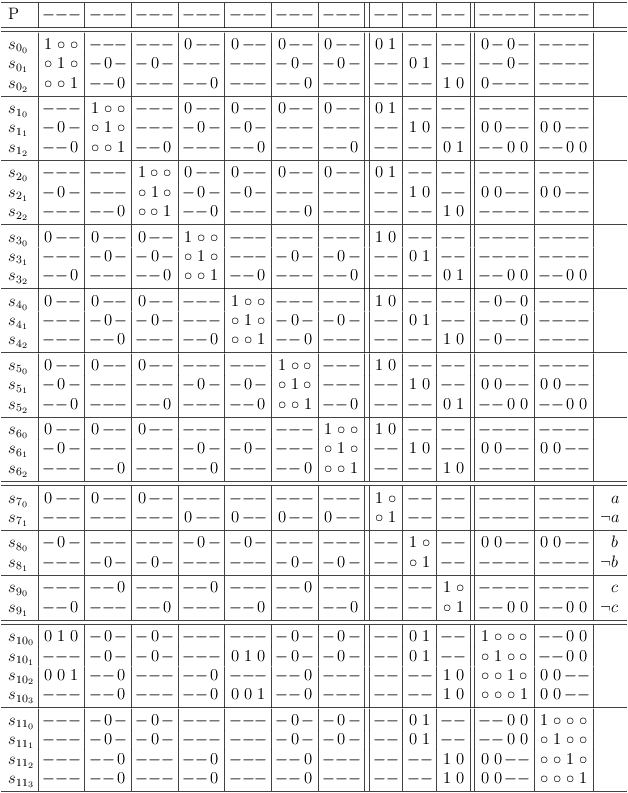
the redundancies can be removed (S11):
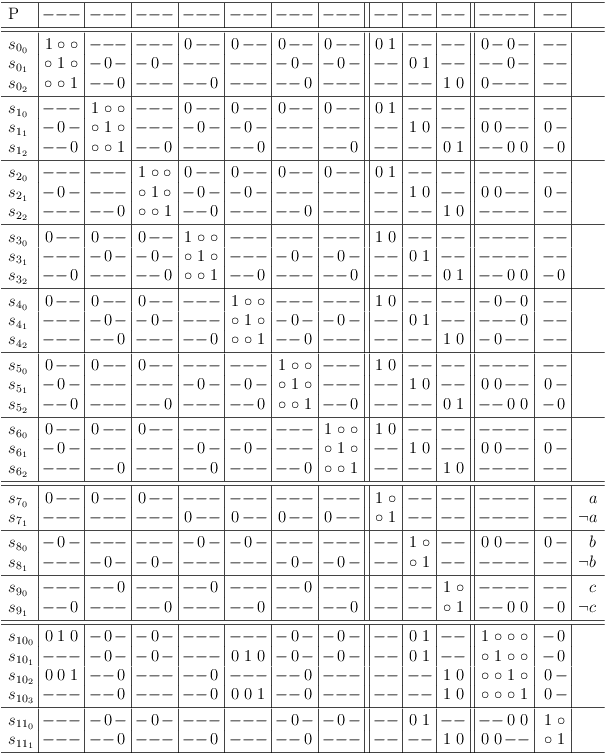
The requirements update algorithm then reveals the single solution for the encoded conjunction:
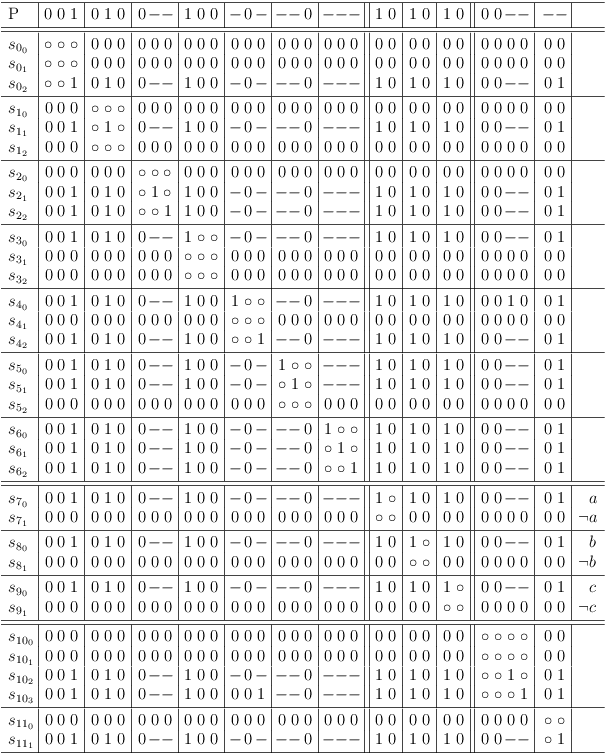
Strange Thing
Here is an example, where conflict maximization gives no further clues. It was constructed after the structure of a Sat-2004 Competition instance handmade/set-85/sat04-838.cnf, (original name hirsch03/hgen8-n260-01-S1597732451.shuffled-as.sat03-885.cnf)
The odd thing about it is that conflicts appear to be transitive, i.e.:
cfl(a, b) ∧ cfl(b, c) → cfl(a, c)
This is different from the common behavior of single variable conflicts:
cfl(a, b) ∧ cfl(b, c) → b = ¬a ∧ c = ¬b → c = ¬¬a = a
However, it is not uncommon with nested conjunction/disjunction/conjunction clauses:
((a ∧ b) ∨ (c ∧ d)) ∧ ((a ∧ ¬b) ∨ (c ∧ ¬d)) ∧ ((¬a ∧ b) ∨ (c ∧ ¬d)) |:check:| bad example (all generated variables from a clause are mutually exclusive)
SAT Problem:
( a0 ∨ a1 ∨ a2 ) ∧ ( b0 ∨ b1 ∨ b2 ) ∧ ( c0 ∨ c1 ∨ c2 ) ∧ ( d0 ∨ d1 ∨ d2 ) ∧ ( e0 ∨ e1 ∨ e2 ) ∧ ( f0 ∨ f1 ∨ f2 ) ∧ ( g0 ∨ g1 ∨ g2 ) ∧ ( h0 ∨ h1 ∨ h2 ) ∧ ( ¬a0 ∨ ¬b0 ) ∧ ( ¬a0 ∨ ¬c0 ) ∧ ( ¬a1 ∨ ¬d0 ) ∧ ( ¬a1 ∨ ¬e0 ) ∧ ( ¬a2 ∨ ¬g0 ) ∧ ( ¬a2 ∨ ¬h0 ) ∧ ( ¬b0 ∨ ¬c0 ) ∧ ( ¬b1 ∨ ¬d1 ) ∧ ( ¬b1 ∨ ¬e1 ) ∧ ( ¬b2 ∨ ¬c2 ) ∧ ( ¬b2 ∨ ¬e2 ) ∧ ( ¬b2 ∨ ¬f0 ) ∧ ( ¬b2 ∨ ¬h2 ) ∧ ( ¬c1 ∨ ¬f2 ) ∧ ( ¬c1 ∨ ¬g2 ) ∧ ( ¬c2 ∨ ¬e2 ) ∧ ( ¬c2 ∨ ¬f0 ) ∧ ( ¬c2 ∨ ¬h2 ) ∧ ( ¬d0 ∨ ¬e0 ) ∧ ( ¬d1 ∨ ¬e1 ) ∧ ( ¬d2 ∨ ¬f1 ) ∧ ( ¬d2 ∨ ¬g1 ) ∧ ( ¬d2 ∨ ¬h1 ) ∧ ( ¬e2 ∨ ¬f0 ) ∧ ( ¬e2 ∨ ¬h2 ) ∧ ( ¬f0 ∨ ¬h2 ) ∧ ( ¬f1 ∨ ¬g1 ) ∧ ( ¬f1 ∨ ¬h1 ) ∧ ( ¬f2 ∨ ¬g2 ) ∧ ( ¬g0 ∨ ¬h0 ) ∧ ( ¬g1 ∨ ¬h1 )
The restrictions between clauses are fully mutually exclusive. E.g:
A = ( ¬a0 ∨ ¬b0 ) B = ( ¬a0 ∨ ¬c0 ) C = ( ¬b0 ∨ ¬c0 )
| a0 | b0 | c0 | A | B | C | A ∧ B ∧ C |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
The truth table shows, that this can be interpreted as:
X1(a0, b0, c0) ∨ (¬a0 ∧ ¬b0 ∧ ¬c0)
I.e., exactly one of a0, b0, c0 must be selected, or none of them.
The core problem of the plain conversion to a satoku matrix (selection variables not shown):
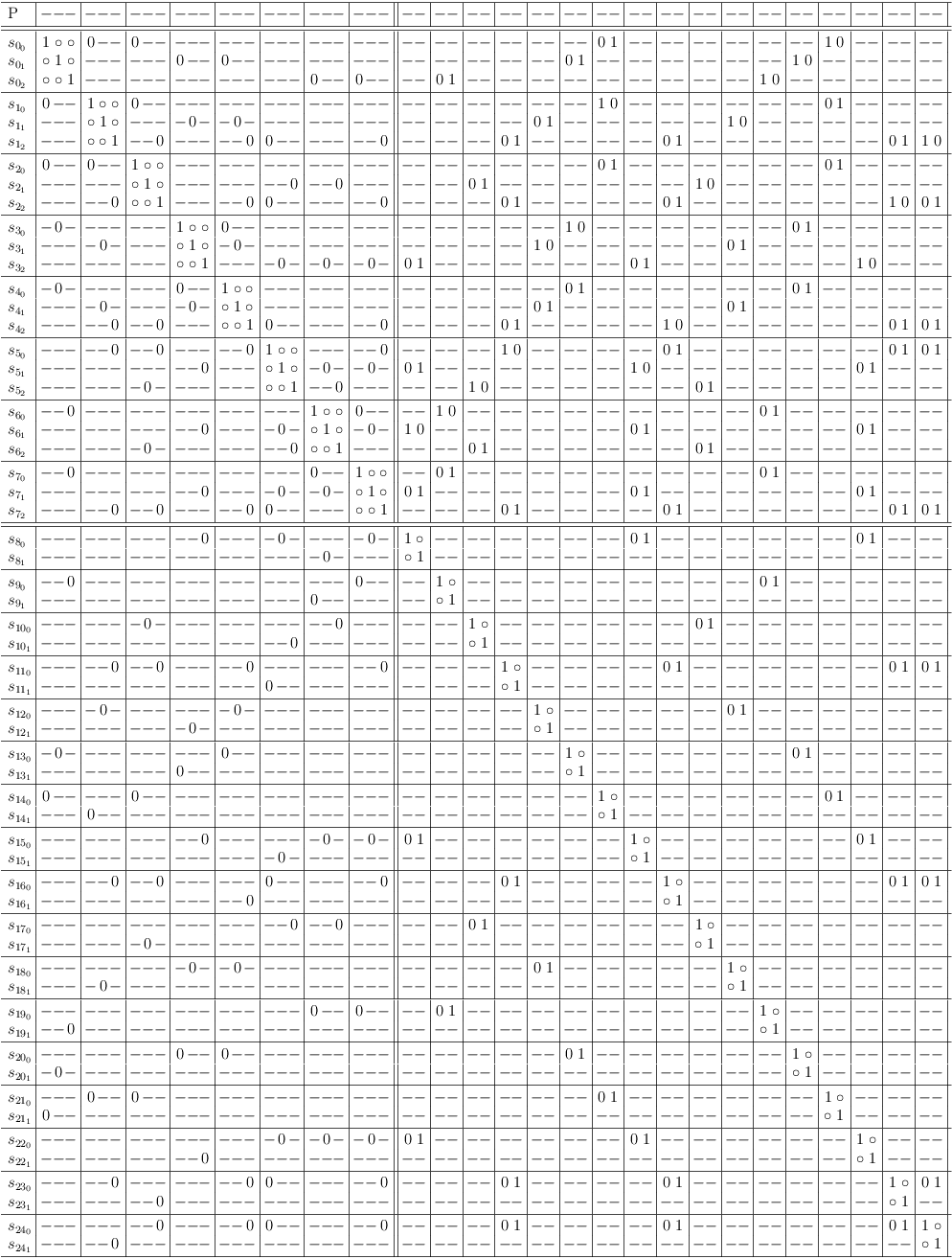
is excatly the same as that of the conversion to a satoku matrix with conflict maximization (variables not shown):
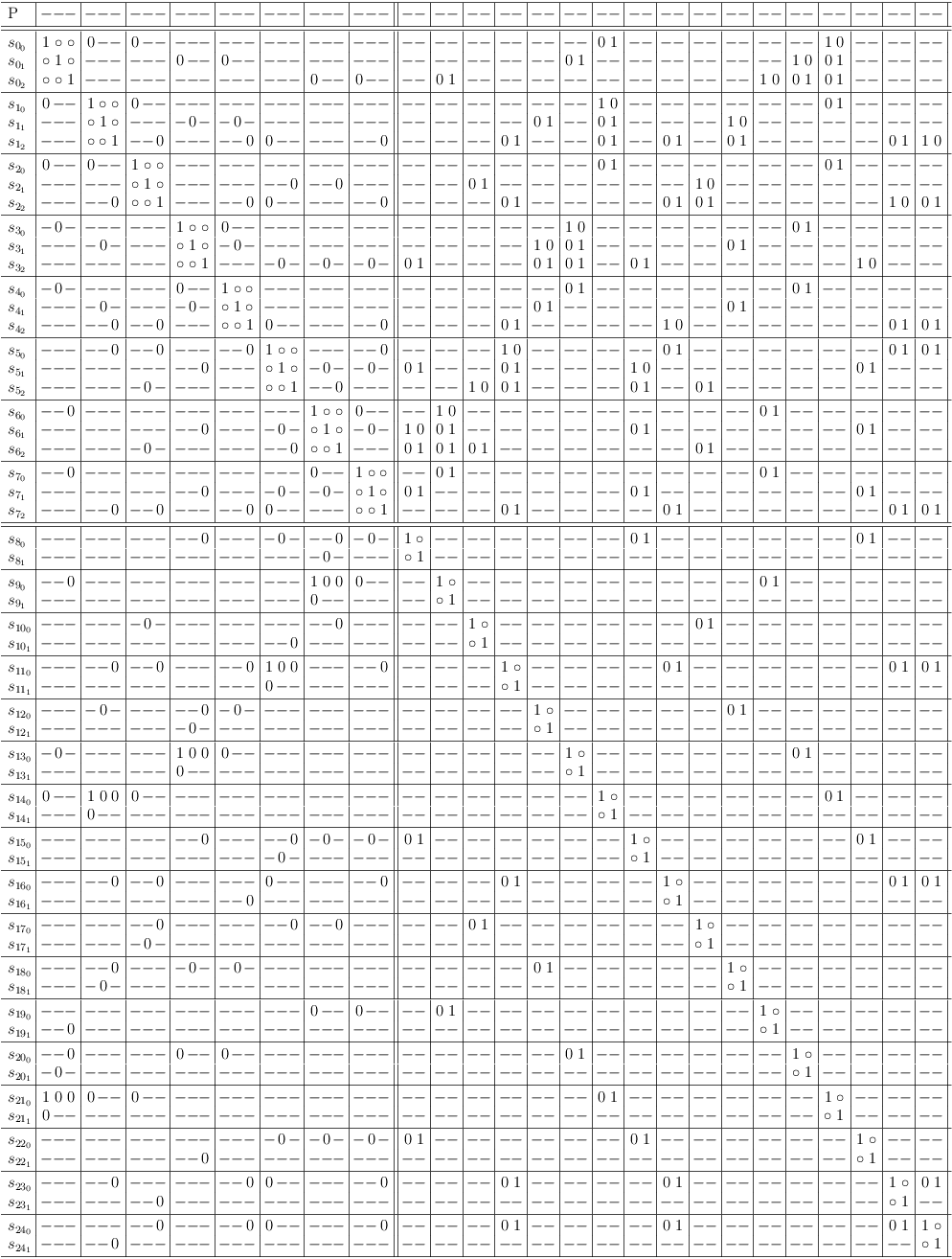
Let's try conflict resolution with a plain satoku matrix.
If 2 variables a, b are members of a SAT problem, it follows, that exactly one pair of the 4 possible variations of unnegated and negated variables must be selected:
a, b ∈ SAT → X1((a ^ b), (¬a ∧ b), (a ∧ ¬b), (¬a ∧ ¬b)) = T
It is therefore allowed to add a clause sub-matrix to the satoku matrix with all variations of a set of variables (only relevant variables shown):
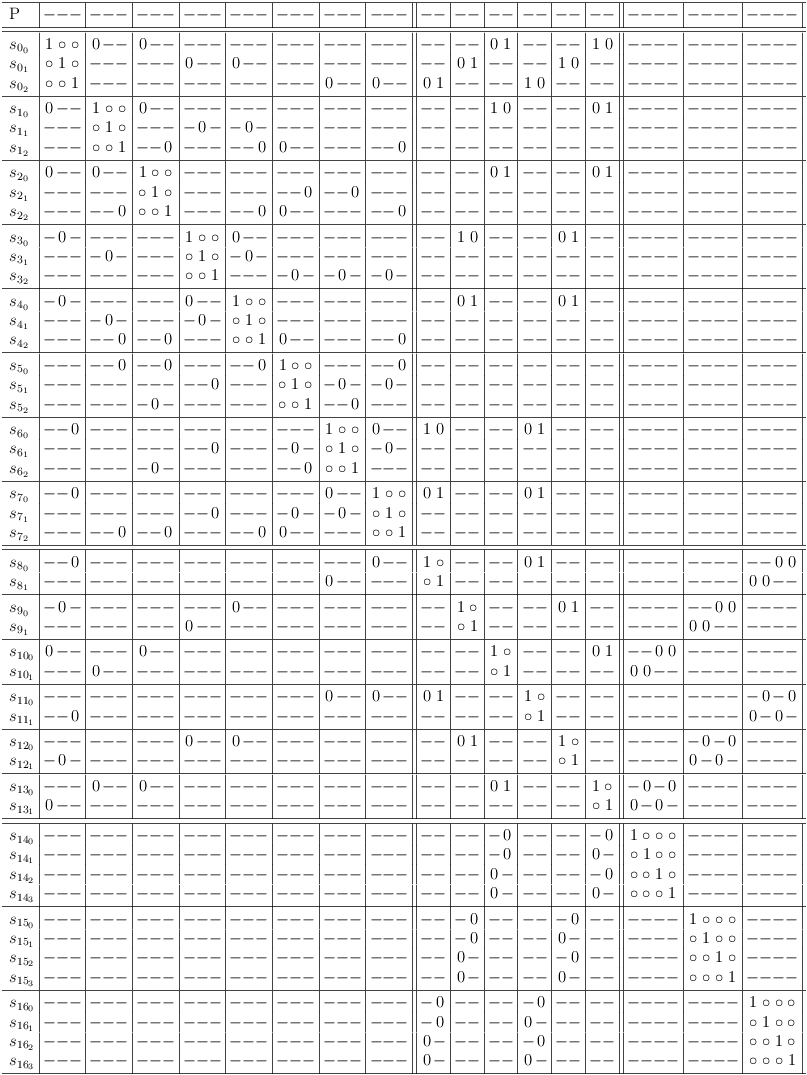
The result, after the requirements update algorithm, is 3 clause sub-matrixes with 3 selection rows each:
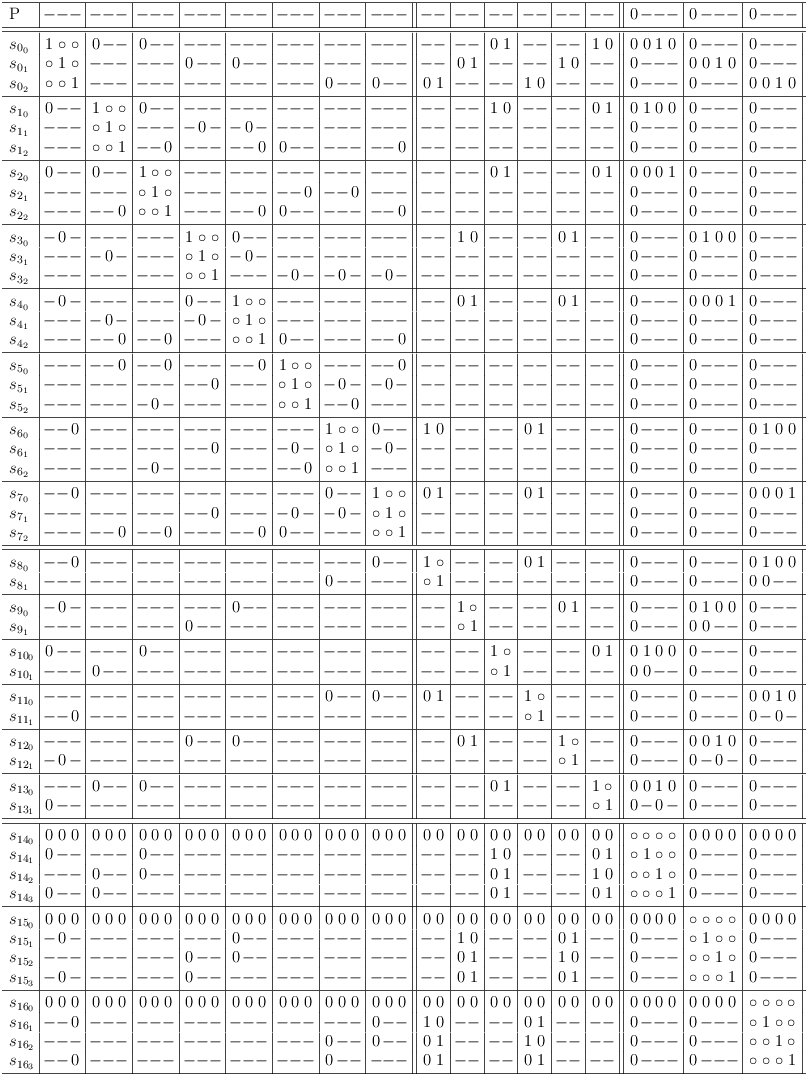
The full conflict resolution presents as follows:
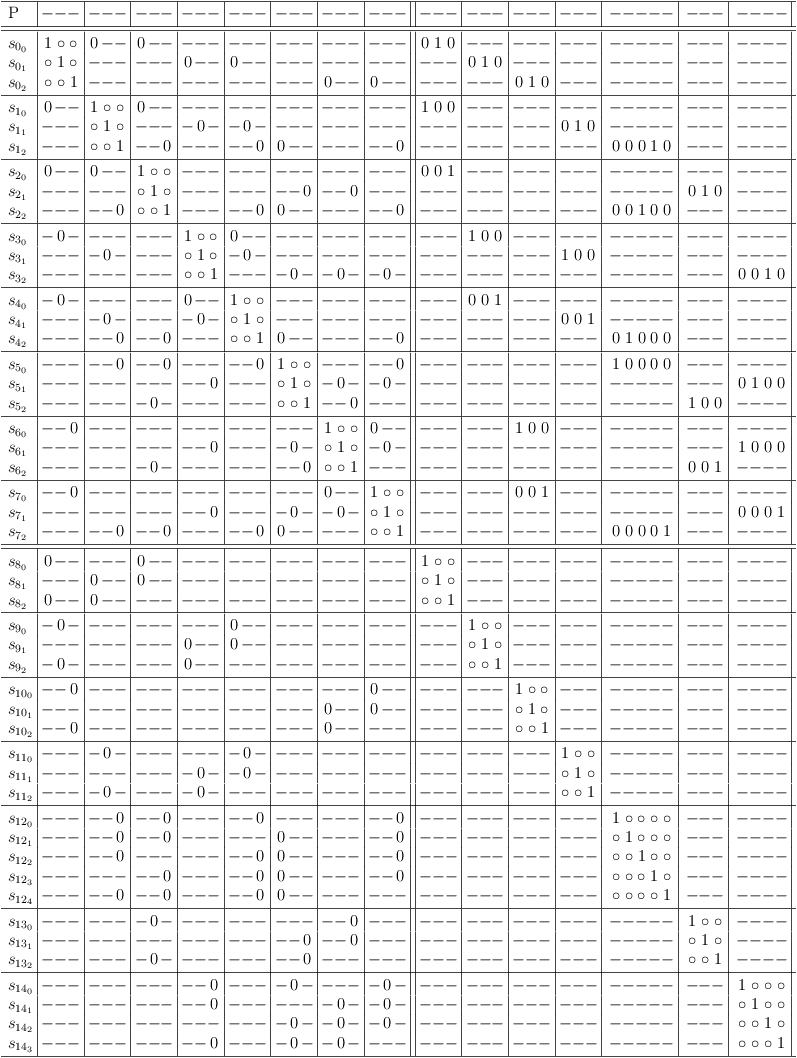
During the next step the new selection row identities are filled in:
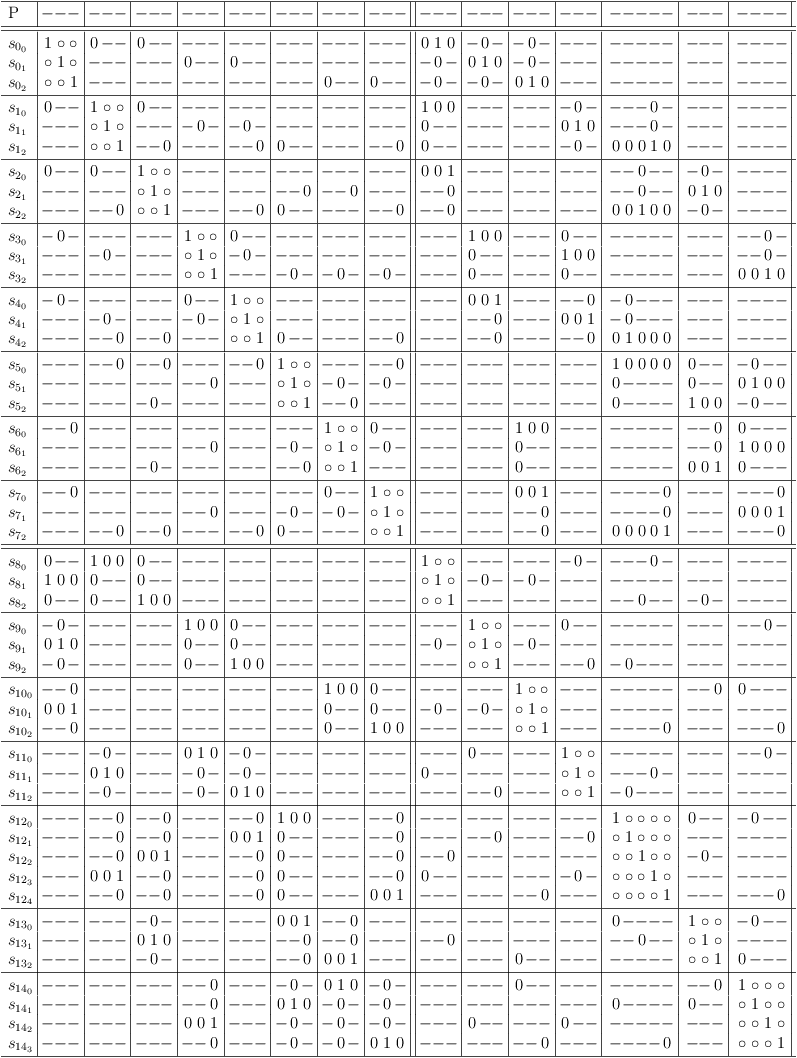
The clause conflict sub-matrixes S[0, 8] and S[1, 8] show, that if clause sub-matrixes S0 and S1 are merged, a dense clause sub-matrix for S8 is produced, where all selection rows of S8 are fully bound (predicted size is 4 selection rows):
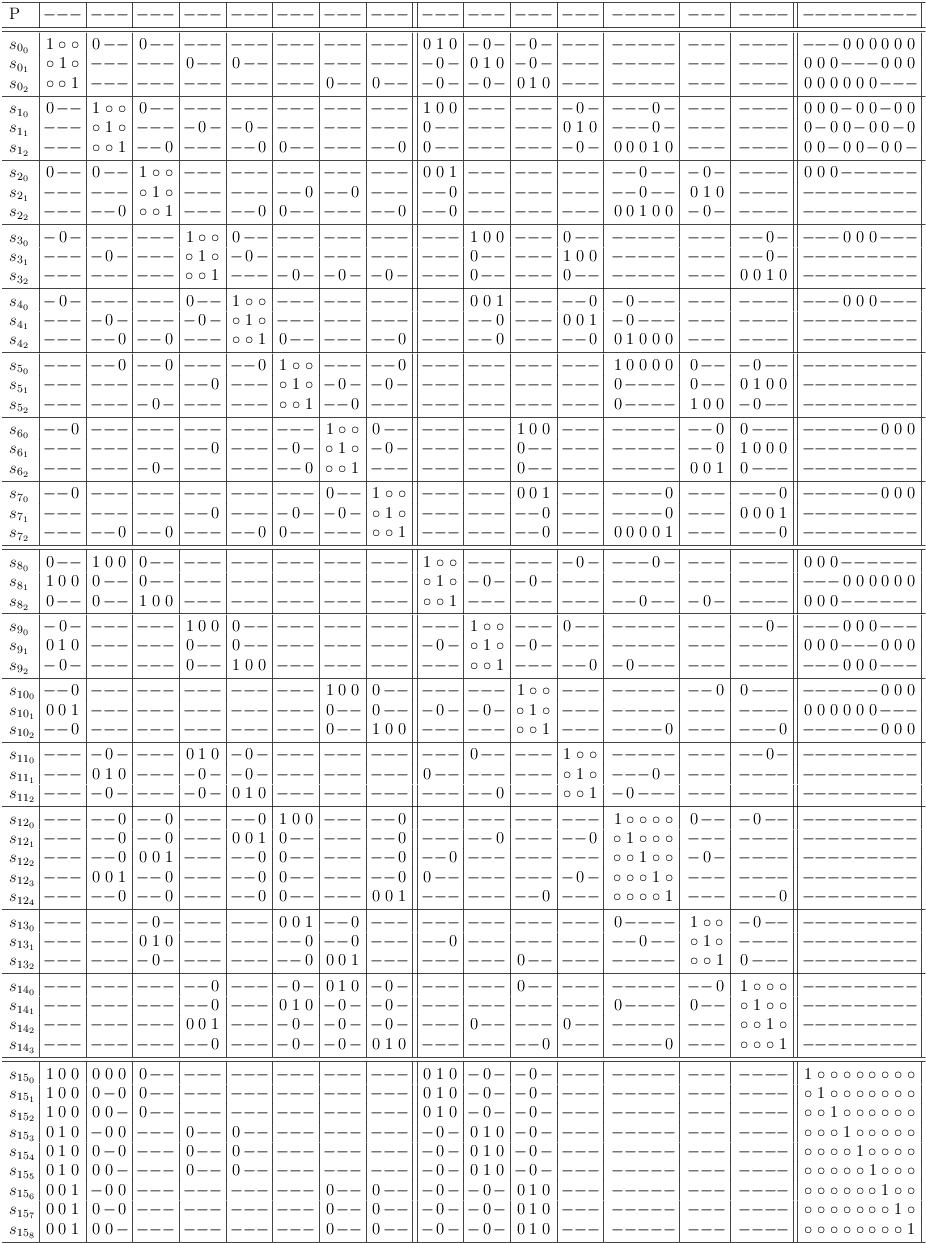
An even better merge choice are clause sub-matrixes S5 and S6, which have two dense conflict clause conflict sub-matrixes in common S(5, 13), S(6, 13) and S(5, 14), S(6, 14):
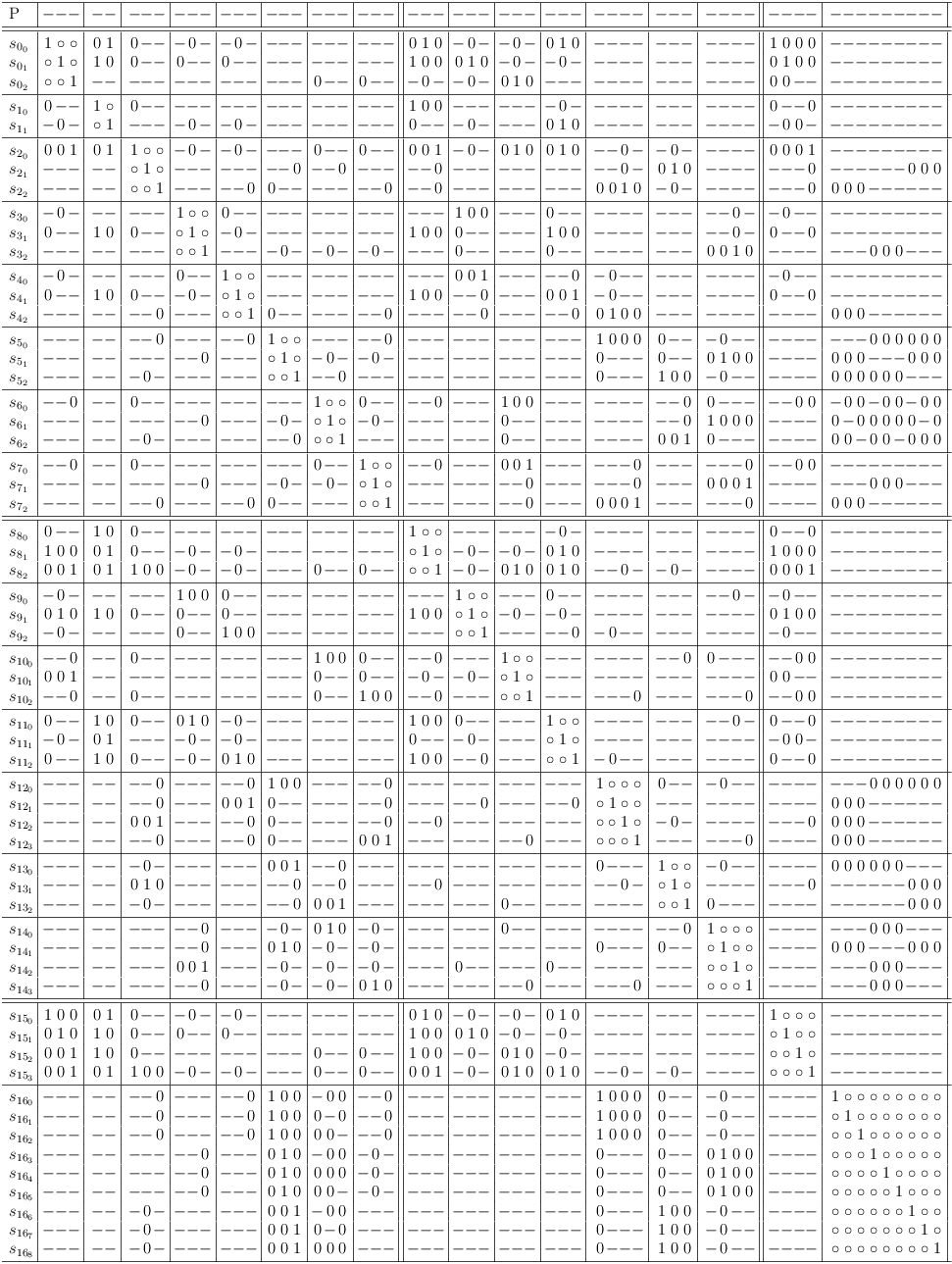
And the contradiction is detected by the requirements update algorithm:

Note: If that combination had been chosen first, it would have lead to the detection of the contradiction by itself.
With alternative reasoning emphasizing standard combinations for complexity reduction:
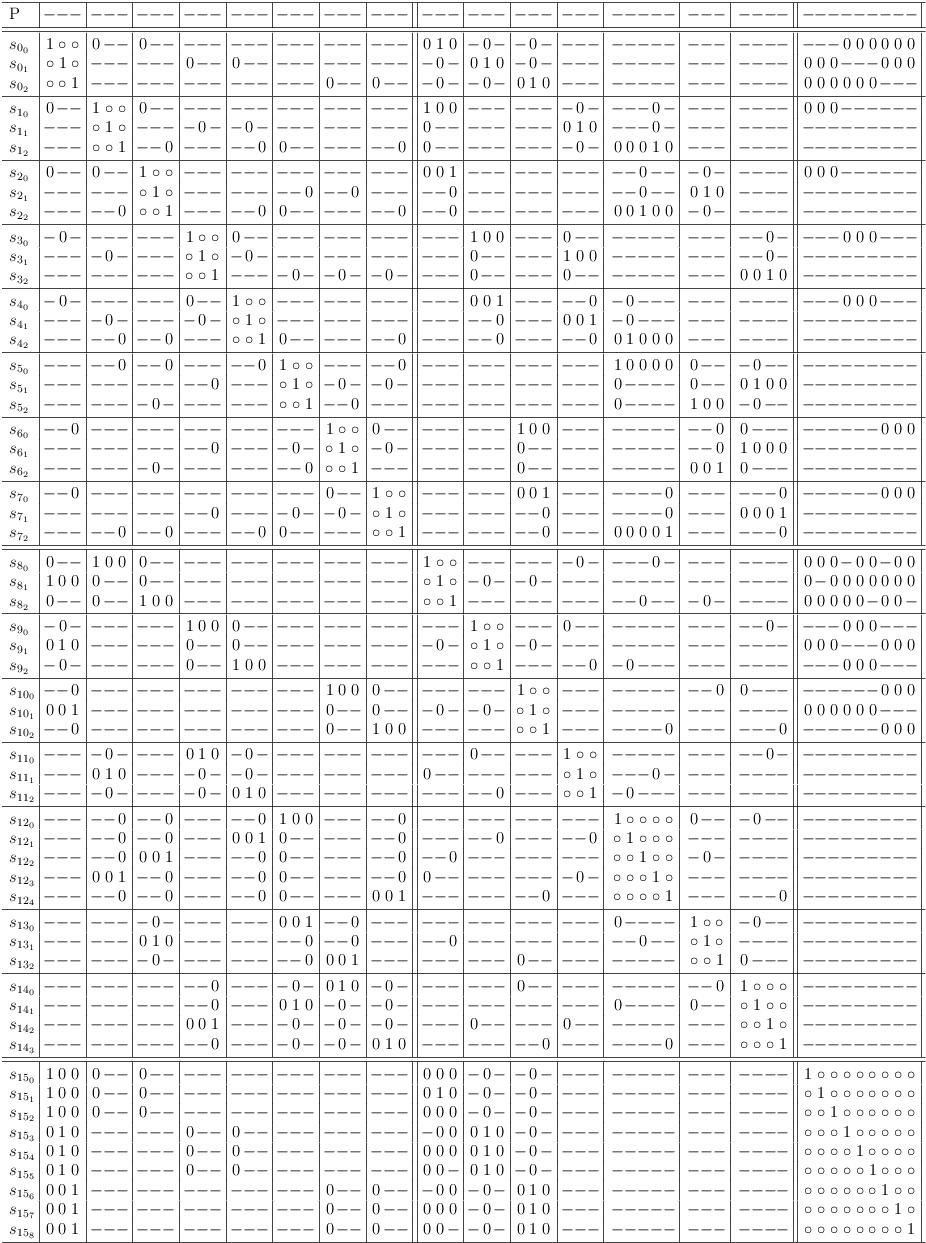
Removing merged clause sub-matrixes:
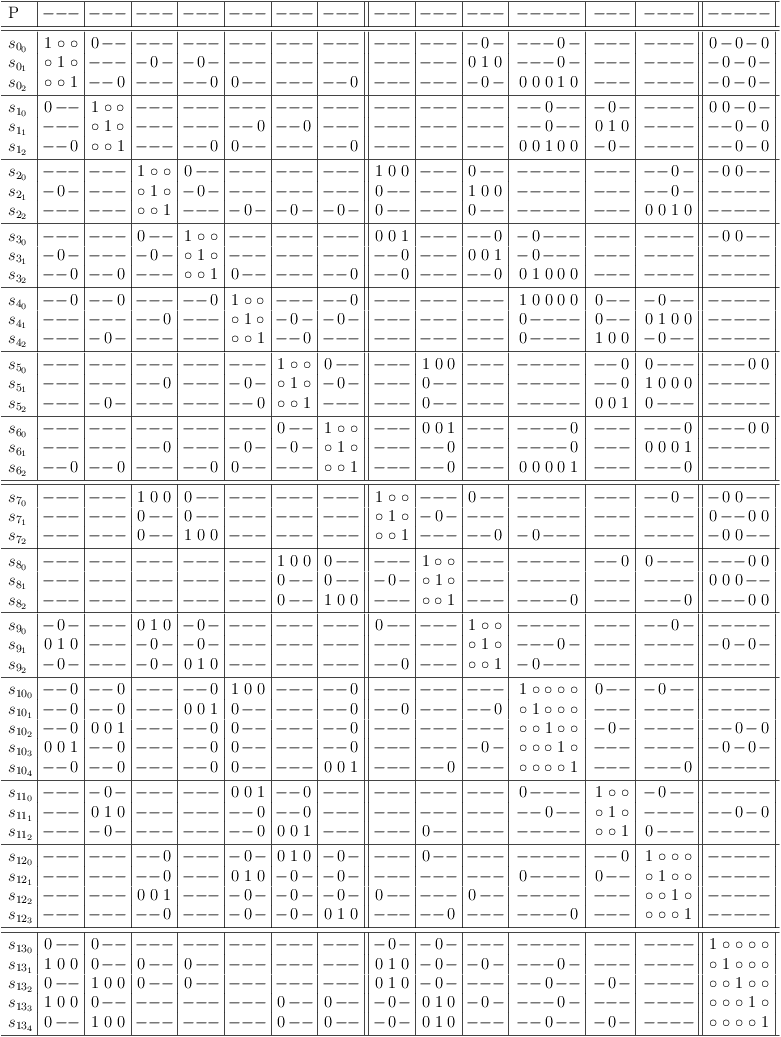
This is as far as you get:
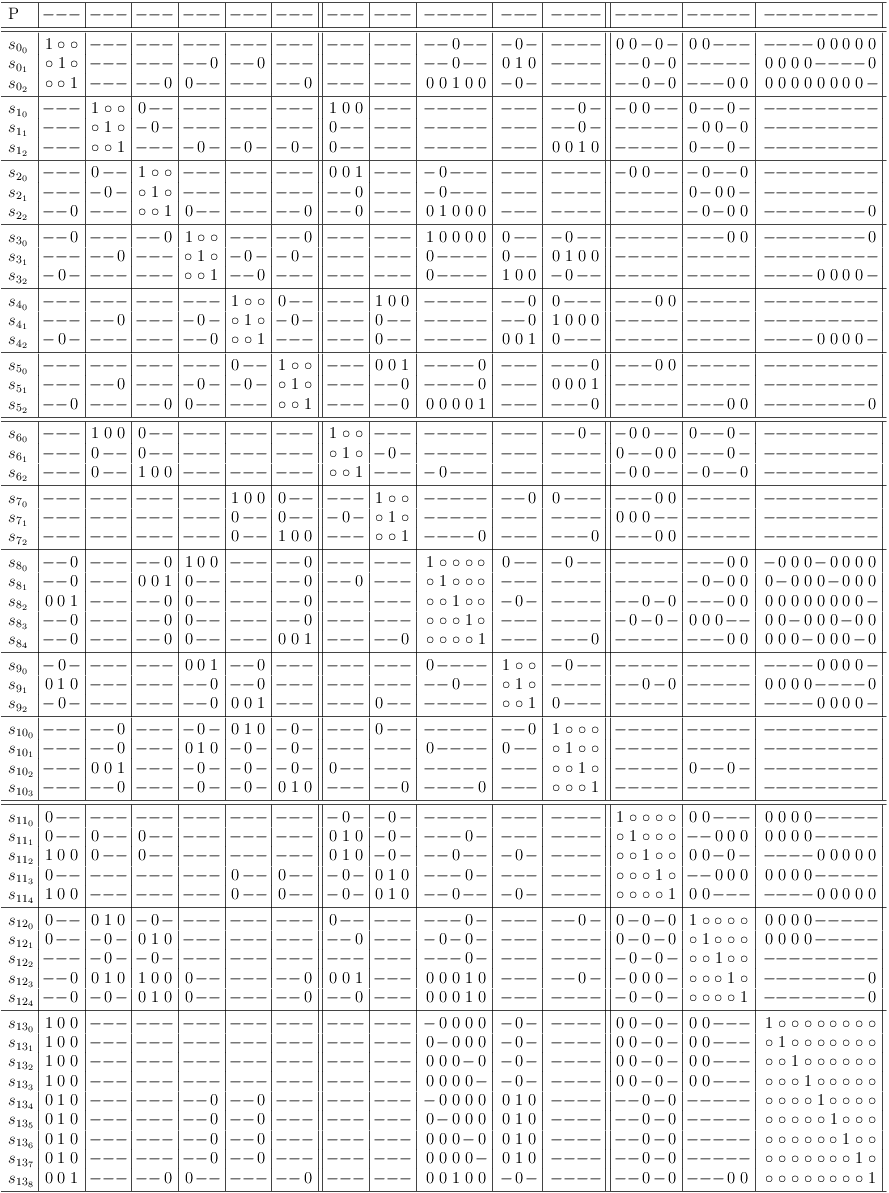
Running the requirements update algorithm leads to a contradiction.
Undriven Clause Learning
The reverse mapping of a solution matrix offers another possibility to go about the problem from Strange Thing.
The 17 different 2-literal restriction clauses of the Strange Thing matrix can be viewed as a set of variables for the SAT core problem. In an unmaximized satoku matrix, the core problem clauses (k>=3) are fully defined by this new set of variables.
A SAT problem can be derived, which has the following structure (|:todo:| make this mathematical):
((l0,0,0 & l0,0,1 & ..) v (l0,1,0 & l0,1,1 & ..) v .. ) & ((l1,0,0 & l1,0,1 & ..) v (l1,1,0 & l1,1,1 & ..) v .. ) & ...
Each segment of a selection row spanning the clause conflict sub-matrixes of the variable section can be translated into a conjunctive clause vector. The resulting set of clause vectors represents a disjunctive set of clauses. The clause vector mapping of the above clause sub-matrixes looks like this:
// C0: DNF: (l06 & l13) v (l05 & l12) v (l01 & l11) [ - - - - - - 0 - - - - - - 1 - - - ] [ - - - - - 0 - - - - - - 1 - - - - ] [ - 0 - - - - - - - - - 1 - - - - - ] l l l l l l l l l l l l l l l l l 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 // C1: [ - - - - - - 1 - - - - - - 0 - - - ] [ - - - - 0 - - - - - 1 - - - - - - ] [ - - - 0 - - - - 0 - - - - - - 0 1 ] // C2: [ - - - - - - 0 - - - - - - 0 - - - ] [ - - 0 - - - - - - 1 - - - - - - - ] [ - - - 0 - - - - 0 - - - - - - 1 0 ] // C3: [ - - - - - 1 - - - - - - 0 - - - - ] [ - - - - 1 - - - - - 0 - - - - - - ] [ 0 - - - - - - 0 - - - - - - 1 - - ] // C4: [ - - - - - 0 - - - - - - 0 - - - - ] [ - - - - 0 - - - - - 0 - - - - - - ] [ - - - 0 - - - - 1 - - - - - - 0 0 ] // C5: [ - - - 1 - - - - 0 - - - - - - 0 0 ] [ 0 - - - - - - 1 - - - - - - 0 - - ] [ - - 1 - - - - - - 0 - - - - - - - ] // C6: [ - 1 - - - - - - - - - 0 - - - - - ] [ 1 - - - - - - 0 - - - - - - 0 - - ] [ - - 0 - - - - - - 0 - - - - - - - ] // C7: [ - 0 - - - - - - - - - 0 - - - - - ] [ 0 - - - - - - 0 - - - - - - 0 - - ] [ - - - 0 - - - - 0 - - - - - - 0 0 ]
The clause vector complement algorithm converts clause vectors from CNF to DNF and vice versa. For the conjunctive clause vectors of the first clause (DNF):
[ - - - - - - 0 - - - - - - 1 - - - ] [ - - - - - 0 - - - - - - 1 - - - - ] [ - 0 - - - - - - - - - 1 - - - - - ]
it delivers a set of disjunctive clause vectors (CNF):
[ _ _ _ _ _ _ _ _ _ _ _ 1 1 1 _ _ _ ] [ _ _ _ _ _ _ 0 _ _ _ _ 1 1 _ _ _ _ ] [ _ _ _ _ _ 0 _ _ _ _ _ 1 _ 1 _ _ _ ] [ _ _ _ _ _ 0 0 _ _ _ _ 1 _ _ _ _ _ ] [ _ 0 _ _ _ _ _ _ _ _ _ _ 1 1 _ _ _ ] [ _ 0 _ _ _ _ 0 _ _ _ _ _ 1 _ _ _ _ ] [ _ 0 _ _ _ 0 _ _ _ _ _ _ _ 1 _ _ _ ] [ _ 0 _ _ _ 0 0 _ _ _ _ _ _ _ _ _ _ ]
Repeating this procedure for all clauses produces this set of 128 CNF clause vectors (blank lines inserted to visualize clause boundaries):
[ _ _ _ _ _ _ _ _ _ _ _ 1 1 1 _ _ _ ] [ _ _ _ _ _ _ 0 _ _ _ _ 1 1 _ _ _ _ ] [ _ _ _ _ _ 0 _ _ _ _ _ 1 _ 1 _ _ _ ] [ _ _ _ _ _ 0 0 _ _ _ _ 1 _ _ _ _ _ ] [ _ 0 _ _ _ _ _ _ _ _ _ _ 1 1 _ _ _ ] [ _ 0 _ _ _ _ 0 _ _ _ _ _ 1 _ _ _ _ ] [ _ 0 _ _ _ 0 _ _ _ _ _ _ _ 1 _ _ _ ] [ _ 0 _ _ _ 0 0 _ _ _ _ _ _ _ _ _ _ ] [ _ _ _ _ _ _ _ _ _ _ 1 _ _ 0 _ _ 1 ] [ _ _ _ _ _ _ _ _ _ _ 1 _ _ 0 _ 0 _ ] [ _ _ _ _ _ _ _ _ 0 _ 1 _ _ 0 _ _ _ ] [ _ _ _ _ _ _ 1 _ _ _ 1 _ _ _ _ _ 1 ] [ _ _ _ _ _ _ 1 _ _ _ 1 _ _ _ _ 0 _ ] [ _ _ _ _ _ _ 1 _ 0 _ 1 _ _ _ _ _ _ ] [ _ _ _ _ 0 _ _ _ _ _ _ _ _ 0 _ _ 1 ] [ _ _ _ _ 0 _ _ _ _ _ _ _ _ 0 _ 0 _ ] [ _ _ _ _ 0 _ _ _ 0 _ _ _ _ 0 _ _ _ ] [ _ _ _ _ 0 _ 1 _ _ _ _ _ _ _ _ _ 1 ] [ _ _ _ _ 0 _ 1 _ _ _ _ _ _ _ _ 0 _ ] [ _ _ _ _ 0 _ 1 _ 0 _ _ _ _ _ _ _ _ ] [ _ _ _ 0 _ _ _ _ _ _ 1 _ _ 0 _ _ _ ] [ _ _ _ 0 _ _ 1 _ _ _ 1 _ _ _ _ _ _ ] [ _ _ _ 0 0 _ _ _ _ _ _ _ _ 0 _ _ _ ] [ _ _ _ 0 0 _ 1 _ _ _ _ _ _ _ _ _ _ ] [ _ _ _ _ _ _ _ _ _ 1 _ _ _ 0 _ _ 0 ] [ _ _ _ _ _ _ _ _ _ 1 _ _ _ 0 _ 1 _ ] [ _ _ _ _ _ _ _ _ 0 1 _ _ _ 0 _ _ _ ] [ _ _ _ _ _ _ 0 _ _ 1 _ _ _ _ _ _ 0 ] [ _ _ _ _ _ _ 0 _ _ 1 _ _ _ _ _ 1 _ ] [ _ _ _ _ _ _ 0 _ 0 1 _ _ _ _ _ _ _ ] [ _ _ _ 0 _ _ _ _ _ 1 _ _ _ 0 _ _ _ ] [ _ _ _ 0 _ _ 0 _ _ 1 _ _ _ _ _ _ _ ] [ _ _ 0 _ _ _ _ _ _ _ _ _ _ 0 _ _ 0 ] [ _ _ 0 _ _ _ _ _ _ _ _ _ _ 0 _ 1 _ ] [ _ _ 0 _ _ _ _ _ 0 _ _ _ _ 0 _ _ _ ] [ _ _ 0 _ _ _ 0 _ _ _ _ _ _ _ _ _ 0 ] [ _ _ 0 _ _ _ 0 _ _ _ _ _ _ _ _ 1 _ ] [ _ _ 0 _ _ _ 0 _ 0 _ _ _ _ _ _ _ _ ] [ _ _ 0 0 _ _ _ _ _ _ _ _ _ 0 _ _ _ ] [ _ _ 0 0 _ _ 0 _ _ _ _ _ _ _ _ _ _ ] [ _ _ _ _ _ _ _ _ _ _ 0 _ 0 _ 1 _ _ ] [ _ _ _ _ _ _ _ 0 _ _ 0 _ 0 _ _ _ _ ] [ _ _ _ _ _ 1 _ _ _ _ 0 _ _ _ 1 _ _ ] [ _ _ _ _ _ 1 _ 0 _ _ 0 _ _ _ _ _ _ ] [ _ _ _ _ 1 _ _ _ _ _ _ _ 0 _ 1 _ _ ] [ _ _ _ _ 1 _ _ 0 _ _ _ _ 0 _ _ _ _ ] [ _ _ _ _ 1 1 _ _ _ _ _ _ _ _ 1 _ _ ] [ _ _ _ _ 1 1 _ 0 _ _ _ _ _ _ _ _ _ ] [ 0 _ _ _ _ _ _ _ _ _ 0 _ 0 _ _ _ _ ] [ 0 _ _ _ _ 1 _ _ _ _ 0 _ _ _ _ _ _ ] [ 0 _ _ _ 1 _ _ _ _ _ _ _ 0 _ _ _ _ ] [ 0 _ _ _ 1 1 _ _ _ _ _ _ _ _ _ _ _ ] [ _ _ _ _ _ _ _ _ _ _ 0 _ 0 _ _ _ 0 ] [ _ _ _ _ _ _ _ _ _ _ 0 _ 0 _ _ 0 _ ] [ _ _ _ _ _ _ _ _ 1 _ 0 _ 0 _ _ _ _ ] [ _ _ _ _ _ 0 _ _ _ _ 0 _ _ _ _ _ 0 ] [ _ _ _ _ _ 0 _ _ _ _ 0 _ _ _ _ 0 _ ] [ _ _ _ _ _ 0 _ _ 1 _ 0 _ _ _ _ _ _ ] [ _ _ _ _ 0 _ _ _ _ _ _ _ 0 _ _ _ 0 ] [ _ _ _ _ 0 _ _ _ _ _ _ _ 0 _ _ 0 _ ] [ _ _ _ _ 0 _ _ _ 1 _ _ _ 0 _ _ _ _ ] [ _ _ _ _ 0 0 _ _ _ _ _ _ _ _ _ _ 0 ] [ _ _ _ _ 0 0 _ _ _ _ _ _ _ _ _ 0 _ ] [ _ _ _ _ 0 0 _ _ 1 _ _ _ _ _ _ _ _ ] [ _ _ _ 0 _ _ _ _ _ _ 0 _ 0 _ _ _ _ ] [ _ _ _ 0 _ 0 _ _ _ _ 0 _ _ _ _ _ _ ] [ _ _ _ 0 0 _ _ _ _ _ _ _ 0 _ _ _ _ ] [ _ _ _ 0 0 0 _ _ _ _ _ _ _ _ _ _ _ ] [ _ _ _ _ _ _ _ _ _ 0 _ _ _ _ 0 _ 0 ] [ _ _ _ _ _ _ _ _ _ 0 _ _ _ _ 0 0 _ ] [ _ _ _ _ _ _ _ _ 0 0 _ _ _ _ 0 _ _ ] [ _ _ _ _ _ _ _ 1 _ 0 _ _ _ _ _ _ 0 ] [ _ _ _ _ _ _ _ 1 _ 0 _ _ _ _ _ 0 _ ] [ _ _ _ _ _ _ _ 1 0 0 _ _ _ _ _ _ _ ] [ _ _ _ 1 _ _ _ _ _ 0 _ _ _ _ 0 _ _ ] [ _ _ _ 1 _ _ _ 1 _ 0 _ _ _ _ _ _ _ ] [ _ _ 1 _ _ _ _ _ _ _ _ _ _ _ 0 _ 0 ] [ _ _ 1 _ _ _ _ _ _ _ _ _ _ _ 0 0 _ ] [ _ _ 1 _ _ _ _ _ 0 _ _ _ _ _ 0 _ _ ] [ _ _ 1 _ _ _ _ 1 _ _ _ _ _ _ _ _ 0 ] [ _ _ 1 _ _ _ _ 1 _ _ _ _ _ _ _ 0 _ ] [ _ _ 1 _ _ _ _ 1 0 _ _ _ _ _ _ _ _ ] [ _ _ 1 1 _ _ _ _ _ _ _ _ _ _ 0 _ _ ] [ _ _ 1 1 _ _ _ 1 _ _ _ _ _ _ _ _ _ ] [ 0 _ _ _ _ _ _ _ _ 0 _ _ _ _ _ _ 0 ] [ 0 _ _ _ _ _ _ _ _ 0 _ _ _ _ _ 0 _ ] [ 0 _ _ _ _ _ _ _ 0 0 _ _ _ _ _ _ _ ] [ 0 _ _ 1 _ _ _ _ _ 0 _ _ _ _ _ _ _ ] [ 0 _ 1 _ _ _ _ _ _ _ _ _ _ _ _ _ 0 ] [ 0 _ 1 _ _ _ _ _ _ _ _ _ _ _ _ 0 _ ] [ 0 _ 1 _ _ _ _ _ 0 _ _ _ _ _ _ _ _ ] [ 0 _ 1 1 _ _ _ _ _ _ _ _ _ _ _ _ _ ] [ _ _ _ _ _ _ _ _ _ 0 _ 0 _ _ 0 _ _ ] [ _ _ _ _ _ _ _ 0 _ 0 _ 0 _ _ _ _ _ ] [ _ _ 0 _ _ _ _ _ _ _ _ 0 _ _ 0 _ _ ] [ _ _ 0 _ _ _ _ 0 _ _ _ 0 _ _ _ _ _ ] [ _ 1 _ _ _ _ _ _ _ 0 _ _ _ _ 0 _ _ ] [ _ 1 _ _ _ _ _ 0 _ 0 _ _ _ _ _ _ _ ] [ _ 1 0 _ _ _ _ _ _ _ _ _ _ _ 0 _ _ ] [ _ 1 0 _ _ _ _ 0 _ _ _ _ _ _ _ _ _ ] [ 1 _ _ _ _ _ _ _ _ 0 _ 0 _ _ _ _ _ ] [ 1 _ 0 _ _ _ _ _ _ _ _ 0 _ _ _ _ _ ] [ 1 1 _ _ _ _ _ _ _ 0 _ _ _ _ _ _ _ ] [ 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ ] [ _ _ _ _ _ _ _ _ _ _ _ 0 _ _ 0 _ 0 ] [ _ _ _ _ _ _ _ _ _ _ _ 0 _ _ 0 0 _ ] [ _ _ _ _ _ _ _ _ 0 _ _ 0 _ _ 0 _ _ ] [ _ _ _ _ _ _ _ 0 _ _ _ 0 _ _ _ _ 0 ] [ _ _ _ _ _ _ _ 0 _ _ _ 0 _ _ _ 0 _ ] [ _ _ _ _ _ _ _ 0 0 _ _ 0 _ _ _ _ _ ] [ _ _ _ 0 _ _ _ _ _ _ _ 0 _ _ 0 _ _ ] [ _ _ _ 0 _ _ _ 0 _ _ _ 0 _ _ _ _ _ ] [ _ 0 _ _ _ _ _ _ _ _ _ _ _ _ 0 _ 0 ] [ _ 0 _ _ _ _ _ _ _ _ _ _ _ _ 0 0 _ ] [ _ 0 _ _ _ _ _ _ 0 _ _ _ _ _ 0 _ _ ] [ _ 0 _ _ _ _ _ 0 _ _ _ _ _ _ _ _ 0 ] [ _ 0 _ _ _ _ _ 0 _ _ _ _ _ _ _ 0 _ ] [ _ 0 _ _ _ _ _ 0 0 _ _ _ _ _ _ _ _ ] [ _ 0 _ 0 _ _ _ _ _ _ _ _ _ _ 0 _ _ ] [ _ 0 _ 0 _ _ _ 0 _ _ _ _ _ _ _ _ _ ] [ 0 _ _ _ _ _ _ _ _ _ _ 0 _ _ _ _ 0 ] [ 0 _ _ _ _ _ _ _ _ _ _ 0 _ _ _ 0 _ ] [ 0 _ _ _ _ _ _ _ 0 _ _ 0 _ _ _ _ _ ] [ 0 _ _ 0 _ _ _ _ _ _ _ 0 _ _ _ _ _ ] [ 0 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ 0 ] [ 0 0 _ _ _ _ _ _ _ _ _ _ _ _ _ 0 _ ] [ 0 0 _ _ _ _ _ _ 0 _ _ _ _ _ _ _ _ ] [ 0 0 _ 0 _ _ _ _ _ _ _ _ _ _ _ _ _ ]
When this set of clause vectors is mapped to a satoku matrix with conflict maximization, the contradiction is detected immediately.
RT:
For a SAT problem P with core problem clauses C and 2-literal restrictions V the upper bound for the worst case running time of this algorithm is:
|P| * n^k, n = |V|, k = |C|
For k=3 it is < O(n^4). (|:check:| or whatever the correct definition is.)
3,4-SAT Splitting
The undriven clause learning algorithm is a strong argument for the reduction of clause sizes. Otherwise the algorithm would have some kind of exponential behavior in regard to the clause size. (|:check:| not sure how to calculate this?)
The arbitrary polynomial reduction is well known, so I will introduce another method called 3,4-SAT splitting here. It differs slightly from the standard method and is not yet fully researched.
// | || S|| 0| 0|| 1 1 1 1 1 1 1 1 | 1 1 1 1 1 1 1 1 | // +----++----++---+----++-----------------+-----------------+ // +-----+----++---+----++-----------------+-----------------+ // | 0 H| 0|| | || 1 * * * * * * * | 0 0 _ 0 0 _ _ 0 | // | | 1|| | || * 1 * * * * * * | _ 0 0 _ 0 0 0 0 | // | | 2|| | || * * 1 * * * * * | 0 _ 0 0 _ 0 0 _ | // | | 3|| | || * * * 1 * * * * | 0 0 _ 0 0 _ _ 0 | // | | 4|| | || * * * * 1 * * * | 0 0 0 _ 0 0 0 0 | // | | 5|| | || * * * * * 1 * * | _ 0 _ 0 _ 0 0 _ | // | | 6|| | || * * * * * * 1 * | 0 0 0 0 0 _ _ 0 | // | | 7|| | || * * * * * * * 1 | 0 _ 0 _ 0 _ 0 _ | // +-----+----++---+----++-----------------+-----------------+ // | 1 H| 8|| | || 0 _ 0 0 0 _ 0 0 | 1 * * * * * * * | // | | 9|| | || 0 0 _ 0 0 0 0 _ | * 1 * * * * * * | // | | 10|| | || _ 0 0 _ 0 _ 0 0 | * * 1 * * * * * | // | | 11|| | || 0 _ 0 0 _ 0 0 _ | * * * 1 * * * * | // | | 12|| | || 0 0 _ 0 0 _ 0 0 | * * * * 1 * * * | // | | 13|| | || _ 0 0 _ 0 0 _ _ | * * * * * 1 * * | // | | 14|| | || _ 0 0 _ 0 0 _ 0 | * * * * * * 1 * | // | | 15|| | || 0 0 _ 0 0 _ 0 _ | * * * * * * * 1 | // +-----+----++---+----++-----------------+-----------------+ // |:info:| move point inside and press `C-u M-x satoku-mode RET'
// | || S|| 0| 0|| 1 1 1 1 1 1 1 1 | 1 1 1 1 1 1 1 1 || 1 1 | 1 1 | 1 1 | 1 1 | 1 1 | 1 1 | 1 1 | 1 1 || 1 1 1 1 | 1 1 1 1 | 1 1 1 1 | 1 1 1 1 || // +----++----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | 0 H| 0|| | || 1 * * * * * * * | 0 0 _ 0 0 _ _ 0 || 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 1|| | || * 1 * * * * * * | _ 0 0 _ 0 0 0 0 || 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 2|| | || * * 1 * * * * * | 0 _ 0 0 _ 0 0 _ || 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 3|| | || * * * 1 * * * * | 0 0 _ 0 0 _ _ 0 || 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 4|| | || * * * * 1 * * * | 0 0 0 1 0 0 0 0 || 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 5|| | || * * * * * 1 * * | _ 0 _ 0 _ 0 0 _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 6|| | || * * * * * * 1 * | 0 0 0 0 0 _ _ 0 || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 7|| | || * * * * * * * 1 | 0 _ 0 _ 0 _ 0 _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | 1 H| 8|| | || 0 _ 0 0 0 _ 0 0 | 1 * * * * * * * || 0 1 | _ _ | 0 1 | 0 1 | 0 1 | _ _ | 0 1 | 0 1 || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 9|| | || 0 0 _ 0 0 0 0 _ | * 1 * * * * * * || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | 0 1 | 0 1 | _ _ || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 10|| | || _ 0 0 _ 0 _ 0 0 | * * 1 * * * * * || _ _ | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | 0 1 || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 11|| | || 0 _ 0 0 _ 0 0 _ | * * * 1 * * * * || 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 12|| | || 0 0 _ 0 0 _ 0 0 | * * * * 1 * * * || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 13|| | || _ 0 0 _ 0 0 _ _ | * * * * * 1 * * || _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | _ _ || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 14|| | || _ 0 0 _ 0 0 _ 0 | * * * * * * 1 * || _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 15|| | || 0 0 _ 0 0 _ 0 _ | * * * * * * * 1 || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 | _ _ || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 16|| | || 1 0 0 0 0 0 0 0 | 0 0 _ 0 0 _ _ 0 || 1 * | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || _ _ 0 0 | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 17|| | || 0 _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || * 1 | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || 0 0 _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 18|| | || 0 1 0 0 0 0 0 0 | _ 0 0 _ 0 0 0 0 || 0 1 | 1 * | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 19|| | || _ 0 _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | * 1 | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 20|| | || 0 0 1 0 0 0 0 0 | 0 _ 0 0 _ 0 0 _ || 0 1 | 0 1 | 1 * | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || _ _ _ _ | _ _ 0 0 | _ _ _ _ | _ _ _ _ || // | | 21|| | || _ _ 0 _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | * 1 | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ _ | 0 0 _ _ | _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 22|| | || 0 0 0 1 0 0 0 0 | 0 0 _ 0 0 _ _ 0 || 0 1 | 0 1 | 0 1 | 1 * | 0 1 | 0 1 | 0 1 | 0 1 || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 23|| | || _ _ _ 0 _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | * 1 | _ _ | _ _ | _ _ | _ _ || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 24|| | || 0 0 0 0 1 0 0 0 | 0 0 0 1 0 0 0 0 || 0 1 | 0 1 | 0 1 | 0 1 | 1 * | 0 1 | 0 1 | 0 1 || _ _ _ _ | _ _ _ _ | _ _ 0 0 | _ _ _ _ || // | | 25|| | || _ _ _ _ 0 _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | * 1 | _ _ | _ _ | _ _ || _ _ _ _ | _ _ _ _ | 0 0 _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 26|| | || 0 0 0 0 0 1 0 0 | _ 0 _ 0 _ 0 0 _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 * | 0 1 | 0 1 || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 27|| | || _ _ _ _ _ 0 _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | * 1 | _ _ | _ _ || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 28|| | || 0 0 0 0 0 0 1 0 | 0 0 0 0 0 _ _ 0 || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 * | 0 1 || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ 0 0 || // | | 29|| | || _ _ _ _ _ _ 0 _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | * 1 | _ _ || _ _ _ _ | _ _ _ _ | _ _ _ _ | 0 0 _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 30|| | || 0 0 0 0 0 0 0 1 | 0 _ 0 _ 0 _ 0 _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 * || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 31|| | || _ _ _ _ _ _ _ 0 | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | * 1 || _ _ _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 32|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ 0 | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || 1 * * * | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 33|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ 0 | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || * 1 * * | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 34|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || 0 _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || * * 1 * | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 35|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || 0 _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || * * * 1 | _ _ _ _ | _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 36|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ 0 | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ _ | 1 * * * | _ _ _ _ | _ _ _ _ || // | | 37|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ 0 | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ _ | * 1 * * | _ _ _ _ | _ _ _ _ || // | | 38|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | 0 _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ _ | * * 1 * | _ _ _ _ | _ _ _ _ || // | | 39|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | 0 _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ _ | * * * 1 | _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 40|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ 0 | _ _ | _ _ | _ _ || _ _ _ _ | _ _ _ _ | 1 * * * | _ _ _ _ || // | | 41|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ 0 | _ _ | _ _ | _ _ || _ _ _ _ | _ _ _ _ | * 1 * * | _ _ _ _ || // | | 42|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | 0 _ | _ _ | _ _ | _ _ || _ _ _ _ | _ _ _ _ | * * 1 * | _ _ _ _ || // | | 43|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | 0 _ | _ _ | _ _ | _ _ || _ _ _ _ | _ _ _ _ | * * * 1 | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 44|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ 0 | _ _ || _ _ _ _ | _ _ _ _ | _ _ _ _ | 1 * * * || // | | 45|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ 0 | _ _ || _ _ _ _ | _ _ _ _ | _ _ _ _ | * 1 * * || // | | 46|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | 0 _ | _ _ || _ _ _ _ | _ _ _ _ | _ _ _ _ | * * 1 * || // | | 47|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | 0 _ | _ _ || _ _ _ _ | _ _ _ _ | _ _ _ _ | * * * 1 || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // |:info:| move point inside and press `C-u M-x satoku-mode RET'
// | || S|| 0| 0|| 1 1 1 1 1 1 1 1 | 1 1 1 1 1 1 1 1 || 1 1 | 1 1 | 1 1 | 1 1 | 1 1 | 1 1 | 1 1 | 1 1 || 1 1 1 1 | 1 1 1 1 | 1 1 1 1 | 1 1 1 1 || // +----++----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | 0 H| 0|| | || 1 * * * * * * * | 0 0 _ 0 0 _ _ 0 || 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || _ _ 0 0 | 0 0 _ _ | 0 0 _ _ | 0 0 _ _ || // | | 1|| | || * 1 * * * * * * | _ 0 0 _ 0 0 0 0 || 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 0 0 _ _ | 0 0 _ _ | 0 0 _ _ | 0 0 _ _ || // | | 2|| | || * * 1 * * * * * | 0 _ 0 0 _ 0 0 _ || 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 0 0 _ _ | _ _ 0 0 | 0 0 _ _ | 0 0 _ _ || // | | 3|| | || * * * 1 * * * * | 0 0 _ 0 0 _ _ 0 || 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 || 0 0 _ _ | 0 0 _ _ | 0 0 _ _ | 0 0 _ _ || // | | 4|| | || * * * * 1 * * * | 0 0 0 1 0 0 0 0 || 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 || 0 0 _ _ | 0 0 _ _ | _ _ 0 0 | 0 0 _ _ || // | | 5|| | || * * * * * 1 * * | _ 0 _ 0 _ 0 0 _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 || 0 0 _ _ | 0 0 _ _ | 0 0 _ _ | 0 0 _ _ || // | | 6|| | || * * * * * * 1 * | 0 0 0 0 0 _ _ 0 || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 || 0 0 _ _ | 0 0 _ _ | 0 0 _ _ | _ _ 0 0 || // | | 7|| | || * * * * * * * 1 | 0 _ 0 _ 0 _ 0 _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 || 0 0 _ _ | 0 0 _ _ | 0 0 _ _ | 0 0 _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | 1 H| 8|| | || 0 _ 0 0 0 _ 0 0 | 1 * * * * * * * || 0 1 | _ _ | 0 1 | 0 1 | 0 1 | _ _ | 0 1 | 0 1 || 0 0 _ _ | 0 0 _ _ | 0 0 _ _ | 0 0 _ _ || // | | 9|| | || 0 0 _ 0 0 0 0 _ | * 1 * * * * * * || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | 0 1 | 0 1 | _ _ || 0 0 _ _ | _ _ _ _ | 0 0 _ _ | 0 0 _ _ || // | | 10|| | || _ 0 0 _ 0 _ 0 0 | * * 1 * * * * * || _ _ | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | 0 1 || _ _ _ _ | 0 0 _ _ | 0 0 _ _ | 0 0 _ _ || // | | 11|| | || 0 _ 0 0 _ 0 0 _ | * * * 1 * * * * || 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ || 0 0 _ _ | 0 0 _ _ | _ _ _ _ | 0 0 _ _ || // | | 12|| | || 0 0 _ 0 0 _ 0 0 | * * * * 1 * * * || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 || 0 0 _ _ | _ _ _ _ | 0 0 _ _ | 0 0 _ _ || // | | 13|| | || _ 0 0 _ 0 0 _ _ | * * * * * 1 * * || _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | _ _ || _ _ _ _ | 0 0 _ _ | 0 0 _ _ | _ _ _ _ || // | | 14|| | || _ 0 0 _ 0 0 _ 0 | * * * * * * 1 * || _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 || _ _ _ _ | 0 0 _ _ | 0 0 _ _ | _ _ _ _ || // | | 15|| | || 0 0 _ 0 0 _ 0 _ | * * * * * * * 1 || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 | _ _ || 0 0 _ _ | _ _ _ _ | 0 0 _ _ | 0 0 _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 16|| | || 1 0 0 0 0 0 0 0 | 0 0 _ 0 0 _ _ 0 || 1 * | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || _ _ 0 0 | 0 0 _ _ | 0 0 _ _ | 0 0 _ _ || // | | 17|| | || 0 _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || * 1 | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || 0 0 _ _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 18|| | || 0 1 0 0 0 0 0 0 | _ 0 0 _ 0 0 0 0 || 0 1 | 1 * | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 0 0 _ 0 | 0 0 _ _ | 0 0 _ _ | 0 0 _ _ || // | | 19|| | || _ 0 _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | * 1 | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || 0 _ 0 _ | _ _ _ _ | _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 20|| | || 0 0 1 0 0 0 0 0 | 0 _ 0 0 _ 0 0 _ || 0 1 | 0 1 | 1 * | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 0 0 _ _ | _ _ 0 0 | 0 0 _ _ | 0 0 _ _ || // | | 21|| | || _ _ 0 _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | * 1 | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ _ | 0 0 _ _ | _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 22|| | || 0 0 0 1 0 0 0 0 | 0 0 _ 0 0 _ _ 0 || 0 1 | 0 1 | 0 1 | 1 * | 0 1 | 0 1 | 0 1 | 0 1 || 0 0 _ _ | 0 0 _ 0 | 0 0 _ _ | 0 0 _ _ || // | | 23|| | || _ _ _ 0 _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | * 1 | _ _ | _ _ | _ _ | _ _ || _ _ _ _ | 0 _ 0 _ | _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 24|| | || 0 0 0 0 1 0 0 0 | 0 0 0 1 0 0 0 0 || 0 1 | 0 1 | 0 1 | 0 1 | 1 * | 0 1 | 0 1 | 0 1 || 0 0 _ _ | 0 0 _ _ | _ _ 0 0 | 0 0 _ _ || // | | 25|| | || _ _ _ _ 0 _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | * 1 | _ _ | _ _ | _ _ || _ _ _ _ | _ _ _ _ | 0 0 _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 26|| | || 0 0 0 0 0 1 0 0 | _ 0 _ 0 _ 0 0 _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 * | 0 1 | 0 1 || 0 0 _ _ | 0 0 _ _ | 0 0 _ 0 | 0 0 _ _ || // | | 27|| | || _ _ _ _ _ 0 _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | * 1 | _ _ | _ _ || _ _ _ _ | _ _ _ _ | 0 _ 0 _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 28|| | || 0 0 0 0 0 0 1 0 | 0 0 0 0 0 _ _ 0 || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 * | 0 1 || 0 0 _ _ | 0 0 _ _ | 0 0 _ _ | _ _ 0 0 || // | | 29|| | || _ _ _ _ _ _ 0 _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | * 1 | _ _ || _ _ _ _ | _ _ _ _ | _ _ _ _ | 0 0 _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 30|| | || 0 0 0 0 0 0 0 1 | 0 _ 0 _ 0 _ 0 _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 * || 0 0 _ _ | 0 0 _ _ | 0 0 _ _ | 0 0 _ 0 || // | | 31|| | || _ _ _ _ _ _ _ 0 | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | * 1 || _ _ _ _ | _ _ _ _ | _ _ _ _ | 0 _ 0 _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 32|| | || 1 0 0 0 0 0 0 0 | 0 0 _ 0 0 _ _ 0 || 1 0 | 0 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 1 * * * | 0 0 _ _ | 0 0 _ _ | 0 0 _ _ || // | | 33|| | || 1 0 0 0 0 0 0 0 | 0 0 _ 0 0 _ _ 0 || 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || * 1 * * | 0 0 _ _ | 0 0 _ _ | 0 0 _ _ || // | | 34|| | || 0 _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || 0 1 | _ 0 | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || * * 1 * | _ _ _ _ | _ _ _ _ | _ _ _ _ || // | | 35|| | || 0 _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || 0 1 | 0 _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || * * * 1 | _ _ _ _ | _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 36|| | || 0 0 1 0 0 0 0 0 | 0 _ 0 0 _ 0 0 _ || 0 1 | 0 1 | 1 0 | 0 0 | 0 1 | 0 1 | 0 1 | 0 1 || 0 0 _ _ | 1 * * * | 0 0 _ _ | 0 0 _ _ || // | | 37|| | || 0 0 1 0 0 0 0 0 | 0 _ 0 0 _ 0 0 _ || 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 0 0 _ _ | * 1 * * | 0 0 _ _ | 0 0 _ _ || // | | 38|| | || _ _ 0 _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | 0 1 | _ 0 | _ _ | _ _ | _ _ | _ _ || _ _ _ _ | * * 1 * | _ _ _ _ | _ _ _ _ || // | | 39|| | || _ _ 0 _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | 0 1 | 0 _ | _ _ | _ _ | _ _ | _ _ || _ _ _ _ | * * * 1 | _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 40|| | || 0 0 0 0 1 0 0 0 | 0 0 0 1 0 0 0 0 || 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 0 | 0 1 | 0 1 || 0 0 _ _ | 0 0 _ _ | 1 * * * | 0 0 _ _ || // | | 41|| | || 0 0 0 0 1 0 0 0 | 0 0 0 1 0 0 0 0 || 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 || 0 0 _ _ | 0 0 _ _ | * 1 * * | 0 0 _ _ || // | | 42|| | || _ _ _ _ 0 _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | 0 1 | _ 0 | _ _ | _ _ || _ _ _ _ | _ _ _ _ | * * 1 * | _ _ _ _ || // | | 43|| | || _ _ _ _ 0 _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | 0 1 | 0 _ | _ _ | _ _ || _ _ _ _ | _ _ _ _ | * * * 1 | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // | | 44|| | || 0 0 0 0 0 0 1 0 | 0 0 0 0 0 _ _ 0 || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 0 || 0 0 _ _ | 0 0 _ _ | 0 0 _ _ | 1 * * * || // | | 45|| | || 0 0 0 0 0 0 1 0 | 0 0 0 0 0 _ _ 0 || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 || 0 0 _ _ | 0 0 _ _ | 0 0 _ _ | * 1 * * || // | | 46|| | || _ _ _ _ _ _ 0 _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | 0 1 | _ 0 || _ _ _ _ | _ _ _ _ | _ _ _ _ | * * 1 * || // | | 47|| | || _ _ _ _ _ _ 0 _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | 0 1 | 0 _ || _ _ _ _ | _ _ _ _ | _ _ _ _ | * * * 1 || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++---------+---------+---------+---------++ // |:info:| move point inside and press `C-u M-x satoku-mode RET'
|:todo:| Intermediate table too big.
// | || S|| 0| 0|| 1 1 1 1 1 1 1 1 | 1 1 1 1 1 1 1 1 || 1 1 | 1 1 | 1 1 | 1 1 | 1 1 | 1 1 | 1 1 | 1 1 || 1 1 | 1 1 | 1 1 | 1 1 | 1 1 | 1 1 | 1 1 | 1 1 || 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 || 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 || 1 1 1 1 | 1 1 1 1 || // +----++----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | 0 H| 0|| | || 1 * * * * * * * | 0 0 _ 0 0 _ _ 0 || 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | _ _ | 0 1 || 1 0 0 | 0 0 1 | 0 0 1 | 0 0 1 || 0 0 1 | _ 0 _ | 0 _ _ | _ 0 _ || _ _ _ 0 | 0 0 0 1 || // | | 1|| | || * 1 * * * * * * | _ 0 0 _ 0 0 0 0 || 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | 0 1 | 0 1 || 0 1 0 | 0 0 1 | 0 0 1 | 0 0 1 || _ 0 _ | 0 _ _ | 0 0 1 | 0 0 1 || 0 0 _ _ | 0 0 0 1 || // | | 2|| | || * * 1 * * * * * | 0 _ 0 0 _ 0 0 _ || 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ || 0 0 1 | 1 0 0 | 0 0 1 | 0 0 1 || 0 _ _ | 0 0 1 | _ 0 _ | 0 _ _ || _ _ 0 _ | 0 0 1 0 || // | | 3|| | || * * * 1 * * * * | 0 0 _ 0 0 _ _ 0 || 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | _ _ | 0 1 || 0 0 1 | 0 1 0 | 0 0 1 | 0 0 1 || 0 0 1 | _ 0 _ | 0 _ _ | _ 0 _ || _ _ _ 0 | 0 0 1 0 || // | | 4|| | || * * * * 1 * * * | 0 0 0 1 0 0 0 0 || 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 || 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 || 0 0 1 | 0 0 1 | 1 0 0 | 0 0 1 || 0 0 1 | 0 1 0 | 0 0 1 | 0 0 1 || 0 0 1 0 | 0 1 0 0 || // | | 5|| | || * * * * * 1 * * | _ 0 _ 0 _ 0 0 _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 || _ _ | 0 1 | _ _ | 0 1 | _ _ | 0 1 | 0 1 | _ _ || 0 0 1 | 0 0 1 | 0 1 0 | 0 0 1 || _ 0 _ | _ 0 _ | _ 0 _ | 0 _ _ || _ _ _ _ | 0 1 0 0 || // | | 6|| | || * * * * * * 1 * | 0 0 0 0 0 _ _ 0 || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | _ _ | _ _ | 0 1 || 0 0 1 | 0 0 1 | 0 0 1 | 1 0 0 || 0 0 1 | 0 0 1 | 0 _ _ | _ 0 _ || _ _ 0 0 | 1 0 0 0 || // | | 7|| | || * * * * * * * 1 | 0 _ 0 _ 0 _ 0 _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 || 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ || 0 0 1 | 0 0 1 | 0 0 1 | 0 1 0 || 0 _ _ | 0 _ _ | 0 _ _ | 0 _ _ || _ _ _ _ | 1 0 0 0 || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | 1 H| 8|| | || 0 _ 0 0 0 _ 0 0 | 1 * * * * * * * || 0 1 | _ _ | 0 1 | 0 1 | 0 1 | _ _ | 0 1 | 0 1 || 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 0 _ _ | 0 0 1 | 0 _ _ | 0 0 1 || 1 0 0 | 0 0 1 | 0 0 1 | 0 0 1 || 0 0 0 1 | 0 _ 0 _ || // | | 9|| | || 0 0 _ 0 0 0 0 _ | * 1 * * * * * * || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | 0 1 | 0 1 | _ _ || 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 0 0 1 | _ 0 _ | 0 0 1 | 0 _ _ || 0 1 0 | 0 0 1 | 0 0 1 | 0 0 1 || 0 0 0 1 | _ 0 _ 0 || // | | 10|| | || _ 0 0 _ 0 _ 0 0 | * * 1 * * * * * || _ _ | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | 0 1 || 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || _ 0 _ | 0 _ _ | 0 _ _ | 0 0 1 || 0 0 1 | 1 0 0 | 0 0 1 | 0 0 1 || 0 0 1 0 | 0 _ _ _ || // | | 11|| | || 0 _ 0 0 _ 0 0 _ | * * * 1 * * * * || 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ || 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 || 0 _ _ | 0 0 1 | _ 0 _ | 0 _ _ || 0 0 1 | 0 1 0 | 0 0 1 | 0 0 1 || 0 0 1 0 | _ _ 0 _ || // | | 12|| | || 0 0 _ 0 0 _ 0 0 | * * * * 1 * * * || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 || 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 || 0 0 1 | _ 0 _ | 0 _ _ | 0 0 1 || 0 0 1 | 0 0 1 | 1 0 0 | 0 0 1 || 0 1 0 0 | 0 _ _ 0 || // | | 13|| | || _ 0 0 _ 0 0 _ _ | * * * * * 1 * * || _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | _ _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 || _ 0 _ | 0 _ _ | 0 0 1 | _ _ _ || 0 0 1 | 0 0 1 | 0 1 0 | 0 0 1 || 0 1 0 0 | _ 0 _ _ || // | | 14|| | || _ 0 0 _ 0 0 _ 0 | * * * * * * 1 * || _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 || _ 0 _ | 0 _ _ | 0 0 1 | _ 0 _ || 0 0 1 | 0 0 1 | 0 0 1 | 1 0 0 || 1 0 0 0 | _ 0 _ _ || // | | 15|| | || 0 0 _ 0 0 _ 0 _ | * * * * * * * 1 || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 | _ _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 || 0 0 1 | _ 0 _ | 0 _ _ | 0 _ _ || 0 0 1 | 0 0 1 | 0 0 1 | 0 1 0 || 1 0 0 0 | _ _ _ 0 || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 16|| | || 1 0 0 0 0 0 0 0 | 0 0 _ 0 0 _ _ 0 || 1 * | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | _ _ | 0 1 || 1 0 0 | 0 0 1 | 0 0 1 | 0 0 1 || 0 0 1 | _ 0 _ | 0 _ _ | _ 0 _ || _ _ _ 0 | 0 0 0 1 || // | | 17|| | || 0 _ _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || * 1 | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || 0 _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 18|| | || 0 1 0 0 0 0 0 0 | _ 0 0 _ 0 0 0 0 || 0 1 | 1 * | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | 0 1 | 0 1 || 0 1 0 | 0 0 1 | 0 0 1 | 0 0 1 || _ 0 _ | 0 _ _ | 0 0 1 | 0 0 1 || 0 0 _ _ | 0 0 0 1 || // | | 19|| | || _ 0 _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | * 1 | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ 0 _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 20|| | || 0 0 1 0 0 0 0 0 | 0 _ 0 0 _ 0 0 _ || 0 1 | 0 1 | 1 * | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ || 0 0 1 | 1 0 0 | 0 0 1 | 0 0 1 || 0 _ _ | 0 0 1 | _ 0 _ | 0 _ _ || _ _ 0 _ | 0 0 1 0 || // | | 21|| | || _ _ 0 _ _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | * 1 | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ | 0 _ _ | _ _ _ | _ _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 22|| | || 0 0 0 1 0 0 0 0 | 0 0 _ 0 0 _ _ 0 || 0 1 | 0 1 | 0 1 | 1 * | 0 1 | 0 1 | 0 1 | 0 1 || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | _ _ | 0 1 || 0 0 1 | 0 1 0 | 0 0 1 | 0 0 1 || 0 0 1 | _ 0 _ | 0 _ _ | _ 0 _ || _ _ _ 0 | 0 0 1 0 || // | | 23|| | || _ _ _ 0 _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | * 1 | _ _ | _ _ | _ _ | _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ | _ 0 _ | _ _ _ | _ _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 24|| | || 0 0 0 0 1 0 0 0 | 0 0 0 1 0 0 0 0 || 0 1 | 0 1 | 0 1 | 0 1 | 1 * | 0 1 | 0 1 | 0 1 || 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 || 0 0 1 | 0 0 1 | 1 0 0 | 0 0 1 || 0 0 1 | 0 1 0 | 0 0 1 | 0 0 1 || 0 0 1 0 | 0 1 0 0 || // | | 25|| | || _ _ _ _ 0 _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | * 1 | _ _ | _ _ | _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ | _ _ _ | 0 _ _ | _ _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 26|| | || 0 0 0 0 0 1 0 0 | _ 0 _ 0 _ 0 0 _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 * | 0 1 | 0 1 || _ _ | 0 1 | _ _ | 0 1 | _ _ | 0 1 | 0 1 | _ _ || 0 0 1 | 0 0 1 | 0 1 0 | 0 0 1 || _ 0 _ | _ 0 _ | _ 0 _ | 0 _ _ || _ _ _ _ | 0 1 0 0 || // | | 27|| | || _ _ _ _ _ 0 _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | * 1 | _ _ | _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ | _ _ _ | _ 0 _ | _ _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 28|| | || 0 0 0 0 0 0 1 0 | 0 0 0 0 0 _ _ 0 || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 * | 0 1 || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | _ _ | _ _ | 0 1 || 0 0 1 | 0 0 1 | 0 0 1 | 1 0 0 || 0 0 1 | 0 0 1 | 0 _ _ | _ 0 _ || _ _ 0 0 | 1 0 0 0 || // | | 29|| | || _ _ _ _ _ _ 0 _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | * 1 | _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ | _ _ _ | _ _ _ | 0 _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 30|| | || 0 0 0 0 0 0 0 1 | 0 _ 0 _ 0 _ 0 _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 * || 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ || 0 0 1 | 0 0 1 | 0 0 1 | 0 1 0 || 0 _ _ | 0 _ _ | 0 _ _ | 0 _ _ || _ _ _ _ | 1 0 0 0 || // | | 31|| | || _ _ _ _ _ _ _ 0 | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | * 1 || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ | _ _ _ | _ _ _ | _ 0 _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 64|| | || 0 _ 0 0 0 _ 0 0 | 1 0 0 0 0 0 0 0 || 0 1 | _ _ | 0 1 | 0 1 | 0 1 | _ _ | 0 1 | 0 1 || 1 * | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 0 _ _ | 0 0 1 | 0 _ _ | 0 0 1 || 1 0 0 | 0 0 1 | 0 0 1 | 0 0 1 || 0 0 0 1 | 0 _ 0 _ || // | | 65|| | || _ _ _ _ _ _ _ _ | 0 _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || * 1 | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || 0 _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 66|| | || 0 0 _ 0 0 0 0 _ | 0 1 0 0 0 0 0 0 || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | 0 1 | 0 1 | _ _ || 0 1 | 1 * | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 0 0 1 | _ 0 _ | 0 0 1 | 0 _ _ || 0 1 0 | 0 0 1 | 0 0 1 | 0 0 1 || 0 0 0 1 | _ 0 _ 0 || // | | 67|| | || _ _ _ _ _ _ _ _ | _ 0 _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ | * 1 | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ 0 _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 68|| | || _ 0 0 _ 0 _ 0 0 | 0 0 1 0 0 0 0 0 || _ _ | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | 0 1 || 0 1 | 0 1 | 1 * | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || _ 0 _ | 0 _ _ | 0 _ _ | 0 0 1 || 0 0 1 | 1 0 0 | 0 0 1 | 0 0 1 || 0 0 1 0 | 0 _ _ _ || // | | 69|| | || _ _ _ _ _ _ _ _ | _ _ 0 _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ | _ _ | * 1 | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ | 0 _ _ | _ _ _ | _ _ _ || _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 70|| | || 0 _ 0 0 _ 0 0 _ | 0 0 0 1 0 0 0 0 || 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ || 0 1 | 0 1 | 0 1 | 1 * | 0 1 | 0 1 | 0 1 | 0 1 || 0 _ _ | 0 0 1 | _ 0 _ | 0 _ _ || 0 0 1 | 0 1 0 | 0 0 1 | 0 0 1 || 0 0 1 0 | _ _ 0 _ || // | | 71|| | || _ _ _ _ 0 _ _ _ | _ _ _ 0 _ _ _ _ || _ _ | _ _ | _ _ | _ _ | 0 1 | _ _ | _ _ | _ _ || _ _ | _ _ | _ _ | * 1 | _ _ | _ _ | _ _ | _ _ || _ _ _ | _ _ _ | 0 _ _ | _ _ _ || _ _ _ | _ 0 _ | _ _ _ | _ _ _ || _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 72|| | || 0 0 _ 0 0 _ 0 0 | 0 0 0 0 1 0 0 0 || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 || 0 1 | 0 1 | 0 1 | 0 1 | 1 * | 0 1 | 0 1 | 0 1 || 0 0 1 | _ 0 _ | 0 _ _ | 0 0 1 || 0 0 1 | 0 0 1 | 1 0 0 | 0 0 1 || 0 1 0 0 | 0 _ _ 0 || // | | 73|| | || _ _ _ _ _ _ _ _ | _ _ _ _ 0 _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ | _ _ | _ _ | _ _ | * 1 | _ _ | _ _ | _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ | _ _ _ | 0 _ _ | _ _ _ || _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 74|| | || _ 0 0 _ 0 0 _ _ | 0 0 0 0 0 1 0 0 || _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | _ _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 * | 0 1 | 0 1 || _ 0 _ | 0 _ _ | 0 0 1 | _ _ _ || 0 0 1 | 0 0 1 | 0 1 0 | 0 0 1 || 0 1 0 0 | _ 0 _ _ || // | | 75|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ 0 _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | * 1 | _ _ | _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ | _ _ _ | _ 0 _ | _ _ _ || _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 76|| | || _ 0 0 _ 0 0 _ 0 | 0 0 0 0 0 0 1 0 || _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 * | 0 1 || _ 0 _ | 0 _ _ | 0 0 1 | _ 0 _ || 0 0 1 | 0 0 1 | 0 0 1 | 1 0 0 || 1 0 0 0 | _ 0 _ _ || // | | 77|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ 0 _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | * 1 | _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ | _ _ _ | _ _ _ | 0 _ _ || _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 78|| | || 0 0 _ 0 0 _ 0 _ | 0 0 0 0 0 0 0 1 || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 | _ _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 * || 0 0 1 | _ 0 _ | 0 _ _ | 0 _ _ || 0 0 1 | 0 0 1 | 0 0 1 | 0 1 0 || 1 0 0 0 | _ _ _ 0 || // | | 79|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ _ 0 || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | * 1 || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ | _ _ _ | _ _ _ | _ 0 _ || _ _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 96|| | || 1 0 0 0 0 0 0 0 | 0 0 _ 0 0 _ _ 0 || 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | _ _ | 0 1 || 1 * * | 0 0 1 | 0 0 1 | 0 0 1 || 0 0 1 | _ 0 _ | 0 _ _ | _ 0 _ || _ _ _ 0 | 0 0 0 1 || // | | 97|| | || 0 1 0 0 0 0 0 0 | _ 0 0 _ 0 0 0 0 || 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | 0 1 | 0 1 || * 1 * | 0 0 1 | 0 0 1 | 0 0 1 || _ 0 _ | 0 _ _ | 0 0 1 | 0 0 1 || 0 0 _ _ | 0 0 0 1 || // | | 98|| | || 0 0 _ _ _ _ _ _ | _ _ _ _ _ _ _ _ || 0 1 | 0 1 | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || * * 1 | _ _ _ | _ _ _ | _ _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ _ | _ _ _ 0 || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 99|| | || 0 0 1 0 0 0 0 0 | 0 _ 0 0 _ 0 0 _ || 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ || 0 0 1 | 1 * * | 0 0 1 | 0 0 1 || 0 _ _ | 0 0 1 | _ 0 _ | 0 _ _ || _ _ 0 _ | 0 0 1 0 || // | | 100|| | || 0 0 0 1 0 0 0 0 | 0 0 _ 0 0 _ _ 0 || 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | _ _ | 0 1 || 0 0 1 | * 1 * | 0 0 1 | 0 0 1 || 0 0 1 | _ 0 _ | 0 _ _ | _ 0 _ || _ _ _ 0 | 0 0 1 0 || // | | 101|| | || _ _ 0 0 _ _ _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | 0 1 | 0 1 | _ _ | _ _ | _ _ | _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ | * * 1 | _ _ _ | _ _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ _ | _ _ 0 _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 102|| | || 0 0 0 0 1 0 0 0 | 0 0 0 1 0 0 0 0 || 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 || 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 || 0 0 1 | 0 0 1 | 1 * * | 0 0 1 || 0 0 1 | 0 1 0 | 0 0 1 | 0 0 1 || 0 0 1 0 | 0 1 0 0 || // | | 103|| | || 0 0 0 0 0 1 0 0 | _ 0 _ 0 _ 0 0 _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 || _ _ | 0 1 | _ _ | 0 1 | _ _ | 0 1 | 0 1 | _ _ || 0 0 1 | 0 0 1 | * 1 * | 0 0 1 || _ 0 _ | _ 0 _ | _ 0 _ | 0 _ _ || _ _ _ _ | 0 1 0 0 || // | | 104|| | || _ _ _ _ 0 0 _ _ | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | 0 1 | 0 1 | _ _ | _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ | _ _ _ | * * 1 | _ _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ _ | _ 0 _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 105|| | || 0 0 0 0 0 0 1 0 | 0 0 0 0 0 _ _ 0 || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | _ _ | _ _ | 0 1 || 0 0 1 | 0 0 1 | 0 0 1 | 1 * * || 0 0 1 | 0 0 1 | 0 _ _ | _ 0 _ || _ _ 0 0 | 1 0 0 0 || // | | 106|| | || 0 0 0 0 0 0 0 1 | 0 _ 0 _ 0 _ 0 _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 || 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ || 0 0 1 | 0 0 1 | 0 0 1 | * 1 * || 0 _ _ | 0 _ _ | 0 _ _ | 0 _ _ || _ _ _ _ | 1 0 0 0 || // | | 107|| | || _ _ _ _ _ _ 0 0 | _ _ _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | 0 1 | 0 1 || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ | _ _ _ | _ _ _ | * * 1 || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ _ | 0 _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 108|| | || 0 _ 0 0 0 _ 0 0 | 1 0 0 0 0 0 0 0 || 0 1 | _ _ | 0 1 | 0 1 | 0 1 | _ _ | 0 1 | 0 1 || 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 0 _ _ | 0 0 1 | 0 _ _ | 0 0 1 || 1 * * | 0 0 1 | 0 0 1 | 0 0 1 || 0 0 0 1 | 0 _ 0 _ || // | | 109|| | || 0 0 _ 0 0 0 0 _ | 0 1 0 0 0 0 0 0 || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | 0 1 | 0 1 | _ _ || 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 0 0 1 | _ 0 _ | 0 0 1 | 0 _ _ || * 1 * | 0 0 1 | 0 0 1 | 0 0 1 || 0 0 0 1 | _ 0 _ 0 || // | | 110|| | || _ _ _ _ _ _ _ _ | 0 0 _ _ _ _ _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || 0 1 | 0 1 | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || * * 1 | _ _ _ | _ _ _ | _ _ _ || _ _ _ 0 | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 111|| | || _ 0 0 _ 0 _ 0 0 | 0 0 1 0 0 0 0 0 || _ _ | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | 0 1 || 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || _ 0 _ | 0 _ _ | 0 _ _ | 0 0 1 || 0 0 1 | 1 * * | 0 0 1 | 0 0 1 || 0 0 1 0 | 0 _ _ _ || // | | 112|| | || 0 _ 0 0 _ 0 0 _ | 0 0 0 1 0 0 0 0 || 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ || 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 | 0 1 || 0 _ _ | 0 0 1 | _ 0 _ | 0 _ _ || 0 0 1 | * 1 * | 0 0 1 | 0 0 1 || 0 0 1 0 | _ _ 0 _ || // | | 113|| | || _ _ _ _ 0 _ _ _ | _ _ 0 0 _ _ _ _ || _ _ | _ _ | _ _ | _ _ | 0 1 | _ _ | _ _ | _ _ || _ _ | _ _ | 0 1 | 0 1 | _ _ | _ _ | _ _ | _ _ || _ _ _ | _ _ _ | 0 _ _ | _ _ _ || _ _ _ | * * 1 | _ _ _ | _ _ _ || _ _ 0 _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 114|| | || 0 0 _ 0 0 _ 0 0 | 0 0 0 0 1 0 0 0 || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 || 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 | 0 1 || 0 0 1 | _ 0 _ | 0 _ _ | 0 0 1 || 0 0 1 | 0 0 1 | 1 * * | 0 0 1 || 0 1 0 0 | 0 _ _ 0 || // | | 115|| | || _ 0 0 _ 0 0 _ _ | 0 0 0 0 0 1 0 0 || _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | _ _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 | 0 1 || _ 0 _ | 0 _ _ | 0 0 1 | _ _ _ || 0 0 1 | 0 0 1 | * 1 * | 0 0 1 || 0 1 0 0 | _ 0 _ _ || // | | 116|| | || _ _ _ _ _ _ _ _ | _ _ _ _ 0 0 _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ | _ _ | _ _ | _ _ | 0 1 | 0 1 | _ _ | _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ | _ _ _ | * * 1 | _ _ _ || _ 0 _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 117|| | || _ 0 0 _ 0 0 _ 0 | 0 0 0 0 0 0 1 0 || _ _ | 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 | 0 1 || _ 0 _ | 0 _ _ | 0 0 1 | _ 0 _ || 0 0 1 | 0 0 1 | 0 0 1 | 1 * * || 1 0 0 0 | _ 0 _ _ || // | | 118|| | || 0 0 _ 0 0 _ 0 _ | 0 0 0 0 0 0 0 1 || 0 1 | 0 1 | _ _ | 0 1 | 0 1 | _ _ | 0 1 | _ _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 1 0 || 0 0 1 | _ 0 _ | 0 _ _ | 0 _ _ || 0 0 1 | 0 0 1 | 0 0 1 | * 1 * || 1 0 0 0 | _ _ _ 0 || // | | 119|| | || _ _ _ _ _ _ _ _ | _ _ _ _ _ _ 0 0 || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ || _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | 0 1 | 0 1 || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ | _ _ _ | _ _ _ | * * 1 || 0 _ _ _ | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 120|| | || _ 0 _ _ 0 _ _ _ | 0 0 0 0 0 0 _ _ || _ _ | 0 1 | _ _ | _ _ | 0 1 | _ _ | _ _ | _ _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | _ _ | _ _ || _ 0 _ | _ _ _ | 0 _ _ | _ _ _ || 0 0 1 | 0 0 1 | 0 0 1 | _ _ 0 || 1 * * * | _ _ _ _ || // | | 121|| | || _ 0 _ _ 0 _ _ _ | 0 0 0 0 _ _ 0 0 || _ _ | 0 1 | _ _ | _ _ | 0 1 | _ _ | _ _ | _ _ || 0 1 | 0 1 | 0 1 | 0 1 | _ _ | _ _ | 0 1 | 0 1 || _ 0 _ | _ _ _ | 0 _ _ | _ _ _ || 0 0 1 | 0 0 1 | _ _ 0 | 0 0 1 || * 1 * * | _ _ _ _ || // | | 122|| | || _ _ 0 _ _ _ 0 _ | 0 0 _ _ 0 0 0 0 || _ _ | _ _ | 0 1 | _ _ | _ _ | _ _ | 0 1 | _ _ || 0 1 | 0 1 | _ _ | _ _ | 0 1 | 0 1 | 0 1 | 0 1 || _ _ _ | 0 _ _ | _ _ _ | 0 _ _ || 0 0 1 | _ _ 0 | 0 0 1 | 0 0 1 || * * 1 * | _ _ _ _ || // | | 123|| | || 0 _ _ 0 0 _ 0 _ | _ _ 0 0 0 0 0 0 || 0 1 | _ _ | _ _ | 0 1 | 0 1 | _ _ | 0 1 | _ _ || _ _ | _ _ | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || 0 _ _ | _ 0 _ | 0 _ _ | 0 _ _ || _ _ 0 | 0 0 1 | 0 0 1 | 0 0 1 || * * * 1 | _ _ _ _ || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 124|| | || 0 0 0 0 0 0 _ _ | 0 _ 0 _ 0 _ _ _ || 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | _ _ | _ _ || 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | _ _ | _ _ || 0 0 1 | 0 0 1 | 0 0 1 | _ _ 0 || 0 _ _ | 0 _ _ | 0 _ _ | _ _ _ || _ _ _ _ | 1 * * * || // | | 125|| | || 0 0 0 0 _ _ 0 0 | _ 0 _ _ _ 0 0 _ || 0 1 | 0 1 | 0 1 | 0 1 | _ _ | _ _ | 0 1 | 0 1 || _ _ | 0 1 | _ _ | _ _ | _ _ | 0 1 | 0 1 | _ _ || 0 0 1 | 0 0 1 | _ _ 0 | 0 0 1 || _ 0 _ | _ _ _ | _ 0 _ | 0 _ _ || _ _ _ _ | * 1 * * || // | | 126|| | || 0 0 _ _ 0 0 0 0 | 0 _ _ 0 _ _ _ _ || 0 1 | 0 1 | _ _ | _ _ | 0 1 | 0 1 | 0 1 | 0 1 || 0 1 | _ _ | _ _ | 0 1 | _ _ | _ _ | _ _ | _ _ || 0 0 1 | _ _ 0 | 0 0 1 | 0 0 1 || 0 _ _ | _ 0 _ | _ _ _ | _ _ _ || _ _ _ _ | * * 1 * || // | | 127|| | || _ _ 0 0 0 0 0 0 | _ 0 _ _ 0 _ _ 0 || _ _ | _ _ | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 | 0 1 || _ _ | 0 1 | _ _ | _ _ | 0 1 | _ _ | _ _ | 0 1 || _ _ 0 | 0 0 1 | 0 0 1 | 0 0 1 || _ 0 _ | _ _ _ | 0 _ _ | _ 0 _ || _ _ _ _ | * * * 1 || // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // +-----+----++---+----++-----------------+-----------------++-----+-----+-----+-----+-----+-----+-----+-----++-----+-----+-----+-----+-----+-----+-----+-----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // |:info:| move point inside and press `C-u M-x satoku-mode RET'
// | || S|| 0| 0|| 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 || 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 || 1 1 1 1 | 1 1 1 1 || // +----++----++---+----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // +-----+----++---+----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 96|| | || 1 * * | 0 0 1 | 0 0 1 | 0 0 1 || 0 0 1 | _ 0 _ | 0 _ _ | _ 0 _ || _ _ _ 0 | 0 0 0 1 || // | | 97|| | || * 1 * | 0 0 1 | 0 0 1 | 0 0 1 || _ 0 _ | 0 _ _ | 0 0 1 | 0 0 1 || 0 0 _ _ | 0 0 0 1 || // | | 98|| | || * * 1 | _ _ _ | _ _ _ | _ _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ _ | _ _ _ 0 || // +-----+----++---+----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 99|| | || 0 0 1 | 1 * * | 0 0 1 | 0 0 1 || 0 _ _ | 0 0 1 | _ 0 _ | 0 _ _ || _ _ 0 _ | 0 0 1 0 || // | | 100|| | || 0 0 1 | * 1 * | 0 0 1 | 0 0 1 || 0 0 1 | _ 0 _ | 0 _ _ | _ 0 _ || _ _ _ 0 | 0 0 1 0 || // | | 101|| | || _ _ _ | * * 1 | _ _ _ | _ _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ _ | _ _ 0 _ || // +-----+----++---+----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 102|| | || 0 0 1 | 0 0 1 | 1 * * | 0 0 1 || 0 0 1 | 0 1 0 | 0 0 1 | 0 0 1 || 0 0 1 0 | 0 1 0 0 || // | | 103|| | || 0 0 1 | 0 0 1 | * 1 * | 0 0 1 || _ 0 _ | _ 0 _ | _ 0 _ | 0 _ _ || _ _ _ _ | 0 1 0 0 || // | | 104|| | || _ _ _ | _ _ _ | * * 1 | _ _ _ || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ _ | _ 0 _ _ || // +-----+----++---+----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 105|| | || 0 0 1 | 0 0 1 | 0 0 1 | 1 * * || 0 0 1 | 0 0 1 | 0 _ _ | _ 0 _ || _ _ 0 0 | 1 0 0 0 || // | | 106|| | || 0 0 1 | 0 0 1 | 0 0 1 | * 1 * || 0 _ _ | 0 _ _ | 0 _ _ | 0 _ _ || _ _ _ _ | 1 0 0 0 || // | | 107|| | || _ _ _ | _ _ _ | _ _ _ | * * 1 || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ _ | 0 _ _ _ || // +-----+----++---+----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // +-----+----++---+----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 108|| | || 0 _ _ | 0 0 1 | 0 _ _ | 0 0 1 || 1 * * | 0 0 1 | 0 0 1 | 0 0 1 || 0 0 0 1 | 0 _ 0 _ || // | | 109|| | || 0 0 1 | _ 0 _ | 0 0 1 | 0 _ _ || * 1 * | 0 0 1 | 0 0 1 | 0 0 1 || 0 0 0 1 | _ 0 _ 0 || // | | 110|| | || _ _ _ | _ _ _ | _ _ _ | _ _ _ || * * 1 | _ _ _ | _ _ _ | _ _ _ || _ _ _ 0 | _ _ _ _ || // +-----+----++---+----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 111|| | || _ 0 _ | 0 _ _ | 0 _ _ | 0 0 1 || 0 0 1 | 1 * * | 0 0 1 | 0 0 1 || 0 0 1 0 | 0 _ _ _ || // | | 112|| | || 0 _ _ | 0 0 1 | _ 0 _ | 0 _ _ || 0 0 1 | * 1 * | 0 0 1 | 0 0 1 || 0 0 1 0 | _ _ 0 _ || // | | 113|| | || _ _ _ | _ _ _ | 0 _ _ | _ _ _ || _ _ _ | * * 1 | _ _ _ | _ _ _ || _ _ 0 _ | _ _ _ _ || // +-----+----++---+----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 114|| | || 0 0 1 | _ 0 _ | 0 _ _ | 0 0 1 || 0 0 1 | 0 0 1 | 1 * * | 0 0 1 || 0 1 0 0 | 0 _ _ 0 || // | | 115|| | || _ 0 _ | 0 _ _ | 0 0 1 | _ _ _ || 0 0 1 | 0 0 1 | * 1 * | 0 0 1 || 0 1 0 0 | _ 0 _ _ || // | | 116|| | || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ | _ _ _ | * * 1 | _ _ _ || _ 0 _ _ | _ _ _ _ || // +-----+----++---+----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 117|| | || _ 0 _ | 0 _ _ | 0 0 1 | _ 0 _ || 0 0 1 | 0 0 1 | 0 0 1 | 1 * * || 1 0 0 0 | _ 0 _ _ || // | | 118|| | || 0 0 1 | _ 0 _ | 0 _ _ | 0 _ _ || 0 0 1 | 0 0 1 | 0 0 1 | * 1 * || 1 0 0 0 | _ _ _ 0 || // | | 119|| | || _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ _ | _ _ _ | _ _ _ | * * 1 || 0 _ _ _ | _ _ _ _ || // +-----+----++---+----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // +-----+----++---+----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 120|| | || _ 0 _ | _ _ _ | 0 _ _ | _ _ _ || 0 0 1 | 0 0 1 | 0 0 1 | _ _ 0 || 1 * * * | _ _ _ _ || // | | 121|| | || _ 0 _ | _ _ _ | 0 _ _ | _ _ _ || 0 0 1 | 0 0 1 | _ _ 0 | 0 0 1 || * 1 * * | _ _ _ _ || // | | 122|| | || _ _ _ | 0 _ _ | _ _ _ | 0 _ _ || 0 0 1 | _ _ 0 | 0 0 1 | 0 0 1 || * * 1 * | _ _ _ _ || // | | 123|| | || 0 _ _ | _ 0 _ | 0 _ _ | 0 _ _ || _ _ 0 | 0 0 1 | 0 0 1 | 0 0 1 || * * * 1 | _ _ _ _ || // +-----+----++---+----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // | | 124|| | || 0 0 1 | 0 0 1 | 0 0 1 | _ _ 0 || 0 _ _ | 0 _ _ | 0 _ _ | _ _ _ || _ _ _ _ | 1 * * * || // | | 125|| | || 0 0 1 | 0 0 1 | _ _ 0 | 0 0 1 || _ 0 _ | _ _ _ | _ 0 _ | 0 _ _ || _ _ _ _ | * 1 * * || // | | 126|| | || 0 0 1 | _ _ 0 | 0 0 1 | 0 0 1 || 0 _ _ | _ 0 _ | _ _ _ | _ _ _ || _ _ _ _ | * * 1 * || // | | 127|| | || _ _ 0 | 0 0 1 | 0 0 1 | 0 0 1 || _ 0 _ | _ _ _ | 0 _ _ | _ 0 _ || _ _ _ _ | * * * 1 || // +-----+----++---+----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // +-----+----++---+----++-------+-------+-------+-------++-------+-------+-------+-------++---------+---------++ // |:info:| move point inside and press `C-u M-x satoku-mode RET'
Worst Case
|:todo:| mod2-3cage-unsat-9-10: Coincidentally, for an unsatisfiable k-SAT instance based on a bipartite XOR problem, m-complexity = n-complexity = n/3 = 29. I.e. clause based and variable based decisions become equivalent.
|:check:| I think that is the reason for XOR structured problems being so hard. Let's see, whether I can find the right words ...
Informed Decisions
Analyzing the requirements of a possible selection shows what would happen, if a selection is made. This is very helpful for deducing some facts.
The example 3-variable conjunction from above has the following "what if" scenarios among others:
- Selecting s[8, 0] is guaranteed to generate a satoku matrix, which has at most 2 3-row clause sub-matrixes.
- Selecting s[8, 1] is guaranteed to generate a satoku matrix, which has at most 2 3-row clause sub-matrixes.
- Selecting s[8, 2] is guaranteed to generate a satoku matrix, which has at most 3 3-row clause sub-matrixes.
- Selecting s[7, 0] is guaranteed to generate a satoku matrix, which has at most 4 3-row clause sub-matrixes.
- Selecting s[7, 1] is guaranteed to generate a satoku matrix, which has at most 3 3-row clause sub-matrixes.
Since selecting s[8, 0] is equivalent to selecting s[7, 1] as they both represent the same conflict situation, it follows that selecting s[7, 1] will in fact only leave 2 instead of 3 clause sub-matrixes with 3 rows.
Selecting both s[7, 1] and s[8, 1] will leave at most 1 clause sub-matrix with 3 rows. This can be achieved by merging variables S7 and S8 (combining all rows of S7 with all rows of S8) and then selecting the row representing the combination s[7, 1] and s[8, 1].
Since we already know, that this satoku matrix is highly implosive and any decision -- weak or strong -- leads to the final single solution, the merge is done with an extra selection row, which leaves all possiblities open and therefore does not enforce the consequences of the merge[16]:
// | || S || 0| 0|| 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 || 1 1 | 1 1 | 1 1 | 1 1 1 1 1 |
// +-----++---++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+
// | 0 H| 0|| 2| 5|| 1 * * | _ _ _ | _ _ _ | 0 _ _ | 0 _ _ | 0 _ _ | 0 _ _ || 0 1 | _ _ | _ _ | _ _ _ _ _ |
// | | 1|| 2| 5|| * 1 * | _ 0 _ | _ 0 _ | _ _ _ | _ _ _ | _ 0 _ | _ 0 _ || _ _ | 0 1 | _ _ | _ _ _ _ _ |
// | | 2|| 2| 4|| * * 1 | _ _ 0 | _ _ _ | _ _ 0 | _ _ _ | _ _ 0 | _ _ _ || _ _ | _ _ | 1 0 | _ _ _ _ _ |
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+
// | 1 H| 3|| 2| 5|| _ _ _ | 1 * * | _ _ _ | 0 _ _ | 0 _ _ | 0 _ _ | 0 _ _ || 0 1 | _ _ | _ _ | _ _ _ _ _ |
// | | 4|| 2| 4|| _ 0 _ | * 1 * | _ _ _ | _ 0 _ | _ 0 _ | _ _ _ | _ _ _ || _ _ | 1 0 | _ _ | _ _ _ _ _ |
// | | 5|| 2| 5|| _ _ 0 | * * 1 | _ _ 0 | _ _ _ | _ _ 0 | _ _ _ | _ _ 0 || _ _ | _ _ | 0 1 | _ _ _ _ _ |
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+
// | 2 H| 6|| 2| 5|| _ _ _ | _ _ _ | 1 * * | 0 _ _ | 0 _ _ | 0 _ _ | 0 _ _ || 0 1 | _ _ | _ _ | _ _ _ _ _ |
// | | 7|| 2| 4|| _ 0 _ | _ _ _ | * 1 * | _ 0 _ | _ 0 _ | _ _ _ | _ _ _ || _ _ | 1 0 | _ _ | _ _ _ _ _ |
// | | 8|| 2| 4|| _ _ _ | _ _ 0 | * * 1 | _ _ 0 | _ _ _ | _ _ 0 | _ _ _ || _ _ | _ _ | 1 0 | _ _ _ _ _ |
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+
// | 3 H| 9|| 2| 4|| 0 _ _ | 0 _ _ | 0 _ _ | 1 * * | _ _ _ | _ _ _ | _ _ _ || 1 0 | _ _ | _ _ | _ _ _ _ _ |
// | | 10|| 2| 5|| _ _ _ | _ 0 _ | _ 0 _ | * 1 * | _ _ _ | _ 0 _ | _ 0 _ || _ _ | 0 1 | _ _ | _ _ _ _ _ |
// | | 11|| 2| 5|| _ _ 0 | _ _ _ | _ _ 0 | * * 1 | _ _ 0 | _ _ _ | _ _ 0 || _ _ | _ _ | 0 1 | _ _ _ _ _ |
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+
// | 4 H| 12|| 2| 4|| 0 _ _ | 0 _ _ | 0 _ _ | _ _ _ | 1 * * | _ _ _ | _ _ _ || 1 0 | _ _ | _ _ | _ _ _ _ _ |
// | | 13|| 2| 5|| _ _ _ | _ 0 _ | _ 0 _ | _ _ _ | * 1 * | _ 0 _ | _ 0 _ || _ _ | 0 1 | _ _ | _ _ _ _ _ |
// | | 14|| 2| 4|| _ _ _ | _ _ 0 | _ _ _ | _ _ 0 | * * 1 | _ _ 0 | _ _ _ || _ _ | _ _ | 1 0 | _ _ _ _ _ |
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+
// | 5 H| 15|| 2| 4|| 0 _ _ | 0 _ _ | 0 _ _ | _ _ _ | _ _ _ | 1 * * | _ _ _ || 1 0 | _ _ | _ _ | _ _ _ _ _ |
// | | 16|| 2| 4|| _ 0 _ | _ _ _ | _ _ _ | _ 0 _ | _ 0 _ | * 1 * | _ _ _ || _ _ | 1 0 | _ _ | _ _ _ _ _ |
// | | 17|| 2| 5|| _ _ 0 | _ _ _ | _ _ 0 | _ _ _ | _ _ 0 | * * 1 | _ _ 0 || _ _ | _ _ | 0 1 | _ _ _ _ _ |
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+
// | 6 H| 18|| 2| 4|| 0 _ _ | 0 _ _ | 0 _ _ | _ _ _ | _ _ _ | _ _ _ | 1 * * || 1 0 | _ _ | _ _ | _ _ _ _ _ |
// | | 19|| 2| 4|| _ 0 _ | _ _ _ | _ _ _ | _ 0 _ | _ 0 _ | _ _ _ | * 1 * || _ _ | 1 0 | _ _ | _ _ _ _ _ |
// | | 20|| 2| 4|| _ _ _ | _ _ 0 | _ _ _ | _ _ 0 | _ _ _ | _ _ 0 | * * 1 || _ _ | _ _ | 1 0 | _ _ _ _ _ |
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+
// | 7 H| 21|| 1| 3|| 0 _ _ | 0 _ _ | 0 _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ || 1 * | _ _ | _ _ | _ _ 0 0 _ | \hphantom{\neg} a
// | | 22|| 1| 4|| _ _ _ | _ _ _ | _ _ _ | 0 _ _ | 0 _ _ | 0 _ _ | 0 _ _ || * 1 | _ _ | _ _ | 0 0 _ _ _ | \neg a
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+
// | 8 H| 23|| 1| 3|| _ 0 _ | _ _ _ | _ _ _ | _ 0 _ | _ 0 _ | _ _ _ | _ _ _ || _ _ | 1 * | _ _ | _ 0 _ 0 _ | \hphantom{\neg} b
// | | 24|| 1| 4|| _ _ _ | _ 0 _ | _ 0 _ | _ _ _ | _ _ _ | _ 0 _ | _ 0 _ || _ _ | * 1 | _ _ | 0 _ 0 _ _ | \neg b
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+
// | 9 H| 25|| 1| 3|| _ _ _ | _ _ 0 | _ _ _ | _ _ 0 | _ _ _ | _ _ 0 | _ _ _ || _ _ | _ _ | 1 * | _ _ _ _ _ | \hphantom{\neg} c
// | | 26|| 1| 4|| _ _ 0 | _ _ _ | _ _ 0 | _ _ _ | _ _ 0 | _ _ _ | _ _ 0 || _ _ | _ _ | * 1 | _ _ _ _ _ | \neg c
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+
// | 10 H| 27|| | || _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ 0 | _ 0 | _ _ | 1 * * * * |
// | | 28|| | || _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ 0 | 0 _ | _ _ | * 1 * * * |
// | | 29|| | || _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ || 0 _ | _ 0 | _ _ | * * 1 * * |
// | | 30|| | || _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ || 0 _ | 0 _ | _ _ | * * * 1 * |
// | | 31|| | || _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ | _ _ | _ _ | * * * * 1 |
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+
// |:info:| move point inside and press `C-u M-x satoku-mode RET'
This technique shows, that the satoku matrix is a very user friendly data structure. It really tries very hard to acommodate to every whim and whisper of its customers.
Setting up all possible variables combinations generates this satoku matrix:
// | || S || 0| 0|| 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 || 1 1 | 1 1 | 1 1 | 1 0 0 0 1 | 1 0 0 0 1 | 1 0 0 0 1 |
// +-----++---++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+-----------+-----------+
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+-----------+-----------+
// | 0 H| 0|| 2| 5|| 1 * * | _ _ _ | _ _ _ | 0 _ _ | 0 _ _ | 0 _ _ | 0 _ _ || 0 1 | _ _ | _ _ | 0 0 0 0 1 | 0 0 0 0 1 | 0 0 0 0 1 |
// | | 1|| 2| 5|| * 1 * | _ 0 _ | _ 0 _ | _ _ _ | _ _ _ | _ 0 _ | _ 0 _ || _ _ | 0 1 | _ _ | 0 0 0 0 1 | 0 0 0 0 1 | 0 0 0 0 1 |
// | | 2|| 2| 4|| * * 1 | _ _ 0 | _ _ _ | _ _ 0 | _ _ _ | _ _ 0 | _ _ _ || _ _ | _ _ | 1 0 | _ 0 0 0 _ | _ 0 0 0 _ | _ 0 0 0 _ |
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+-----------+-----------+
// | 1 H| 3|| 2| 5|| _ _ _ | 1 * * | _ _ _ | 0 _ _ | 0 _ _ | 0 _ _ | 0 _ _ || 0 1 | _ _ | _ _ | 0 0 0 0 1 | 0 0 0 0 1 | 0 0 0 0 1 |
// | | 4|| 2| 4|| _ 0 _ | * 1 * | _ _ _ | _ 0 _ | _ 0 _ | _ _ _ | _ _ _ || _ _ | 1 0 | _ _ | _ 0 0 0 _ | _ 0 0 0 _ | _ 0 0 0 _ |
// | | 5|| 2| 5|| _ _ 0 | * * 1 | _ _ 0 | _ _ _ | _ _ 0 | _ _ _ | _ _ 0 || _ _ | _ _ | 0 1 | 0 0 0 0 1 | 0 0 0 0 1 | 0 0 0 0 1 |
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+-----------+-----------+
// | 2 H| 6|| 2| 5|| _ _ _ | _ _ _ | 1 * * | 0 _ _ | 0 _ _ | 0 _ _ | 0 _ _ || 0 1 | _ _ | _ _ | 0 0 0 0 1 | 0 0 0 0 1 | 0 0 0 0 1 |
// | | 7|| 2| 4|| _ 0 _ | _ _ _ | * 1 * | _ 0 _ | _ 0 _ | _ _ _ | _ _ _ || _ _ | 1 0 | _ _ | _ 0 0 0 _ | _ 0 0 0 _ | _ 0 0 0 _ |
// | | 8|| 2| 4|| _ _ _ | _ _ 0 | * * 1 | _ _ 0 | _ _ _ | _ _ 0 | _ _ _ || _ _ | _ _ | 1 0 | _ 0 0 0 _ | _ 0 0 0 _ | _ 0 0 0 _ |
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+-----------+-----------+
// | 3 H| 9|| 2| 4|| 0 _ _ | 0 _ _ | 0 _ _ | 1 * * | _ _ _ | _ _ _ | _ _ _ || 1 0 | _ _ | _ _ | _ 0 0 0 _ | _ 0 0 0 _ | _ 0 0 0 _ |
// | | 10|| 2| 5|| _ _ _ | _ 0 _ | _ 0 _ | * 1 * | _ _ _ | _ 0 _ | _ 0 _ || _ _ | 0 1 | _ _ | 0 0 0 0 1 | 0 0 0 0 1 | 0 0 0 0 1 |
// | | 11|| 2| 5|| _ _ 0 | _ _ _ | _ _ 0 | * * 1 | _ _ 0 | _ _ _ | _ _ 0 || _ _ | _ _ | 0 1 | 0 0 0 0 1 | 0 0 0 0 1 | 0 0 0 0 1 |
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+-----------+-----------+
// | 4 H| 12|| 2| 4|| 0 _ _ | 0 _ _ | 0 _ _ | _ _ _ | 1 * * | _ _ _ | _ _ _ || 1 0 | _ _ | _ _ | _ 0 0 0 _ | _ 0 0 0 _ | _ 0 0 0 _ |
// | | 13|| 2| 5|| _ _ _ | _ 0 _ | _ 0 _ | _ _ _ | * 1 * | _ 0 _ | _ 0 _ || _ _ | 0 1 | _ _ | 0 0 0 0 1 | 0 0 0 0 1 | 0 0 0 0 1 |
// | | 14|| 2| 4|| _ _ _ | _ _ 0 | _ _ _ | _ _ 0 | * * 1 | _ _ 0 | _ _ _ || _ _ | _ _ | 1 0 | _ 0 0 0 _ | _ 0 0 0 _ | _ 0 0 0 _ |
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+-----------+-----------+
// | 5 H| 15|| 2| 4|| 0 _ _ | 0 _ _ | 0 _ _ | _ _ _ | _ _ _ | 1 * * | _ _ _ || 1 0 | _ _ | _ _ | _ 0 0 0 _ | _ 0 0 0 _ | _ 0 0 0 _ |
// | | 16|| 2| 4|| _ 0 _ | _ _ _ | _ _ _ | _ 0 _ | _ 0 _ | * 1 * | _ _ _ || _ _ | 1 0 | _ _ | _ 0 0 0 _ | _ 0 0 0 _ | _ 0 0 0 _ |
// | | 17|| 2| 5|| _ _ 0 | _ _ _ | _ _ 0 | _ _ _ | _ _ 0 | * * 1 | _ _ 0 || _ _ | _ _ | 0 1 | 0 0 0 0 1 | 0 0 0 0 1 | 0 0 0 0 1 |
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+-----------+-----------+
// | 6 H| 18|| 2| 4|| 0 _ _ | 0 _ _ | 0 _ _ | _ _ _ | _ _ _ | _ _ _ | 1 * * || 1 0 | _ _ | _ _ | _ 0 0 0 _ | _ 0 0 0 _ | _ 0 0 0 _ |
// | | 19|| 2| 4|| _ 0 _ | _ _ _ | _ _ _ | _ 0 _ | _ 0 _ | _ _ _ | * 1 * || _ _ | 1 0 | _ _ | _ 0 0 0 _ | _ 0 0 0 _ | _ 0 0 0 _ |
// | | 20|| 2| 4|| _ _ _ | _ _ 0 | _ _ _ | _ _ 0 | _ _ _ | _ _ 0 | * * 1 || _ _ | _ _ | 1 0 | _ 0 0 0 _ | _ 0 0 0 _ | _ 0 0 0 _ |
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+-----------+-----------+
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+-----------+-----------+
// | 7 H| 21|| 1| 3|| 0 _ _ | 0 _ _ | 0 _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ || 1 * | _ _ | _ _ | _ 0 0 0 _ | _ 0 0 0 _ | _ 0 0 0 _ | \hphantom{\neg} a
// | | 22|| 1| 4|| _ _ _ | _ _ _ | _ _ _ | 0 _ _ | 0 _ _ | 0 _ _ | 0 _ _ || * 1 | _ _ | _ _ | 0 0 0 0 1 | 0 0 0 0 1 | 0 0 0 0 1 | \neg a
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+-----------+-----------+
// | 8 H| 23|| 1| 3|| _ 0 _ | _ _ _ | _ _ _ | _ 0 _ | _ 0 _ | _ _ _ | _ _ _ || _ _ | 1 * | _ _ | _ 0 0 0 _ | _ 0 0 0 _ | _ 0 0 0 _ | \hphantom{\neg} b
// | | 24|| 1| 4|| _ _ _ | _ 0 _ | _ 0 _ | _ _ _ | _ _ _ | _ 0 _ | _ 0 _ || _ _ | * 1 | _ _ | 0 0 0 0 1 | 0 0 0 0 1 | 0 0 0 0 1 | \neg b
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+-----------+-----------+
// | 9 H| 25|| 1| 3|| _ _ _ | _ _ 0 | _ _ _ | _ _ 0 | _ _ _ | _ _ 0 | _ _ _ || _ _ | _ _ | 1 * | _ 0 0 0 _ | _ 0 0 0 _ | _ 0 0 0 _ | \hphantom{\neg} c
// | | 26|| 1| 4|| _ _ 0 | _ _ _ | _ _ 0 | _ _ _ | _ _ 0 | _ _ _ | _ _ 0 || _ _ | _ _ | * 1 | 0 0 0 0 1 | 0 0 0 0 1 | 0 0 0 0 1 | \neg c
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+-----------+-----------+
// | 10 H| 27|| | || 0 0 1 | 0 1 0 | 0 _ _ | 1 0 0 | _ 0 _ | _ _ 0 | _ _ _ || 1 0 | 1 0 | 1 0 | 1 * * * * | _ 0 0 0 _ | _ 0 0 0 _ |
// | | 28|| | || 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 || 0 0 | 0 0 | 0 0 | * 1 * * * | 0 0 0 0 0 | 0 0 0 0 0 |
// | | 29|| | || 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 || 0 0 | 0 0 | 0 0 | * * 1 * * | 0 0 0 0 0 | 0 0 0 0 0 |
// | | 30|| | || 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 || 0 0 | 0 0 | 0 0 | * * * 1 * | 0 0 0 0 0 | 0 0 0 0 0 |
// | | 31|| | || _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ | _ _ | _ _ | * * * * 1 | _ 0 0 0 _ | _ 0 0 0 _ |
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+-----------+-----------+
// | 11 H| 32|| | || 0 0 1 | 0 1 0 | 0 _ _ | 1 0 0 | _ 0 _ | _ _ 0 | _ _ _ || 1 0 | 1 0 | 1 0 | _ 0 0 0 _ | 1 * * * * | _ 0 0 0 _ |
// | | 33|| | || 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 || 0 0 | 0 0 | 0 0 | 0 0 0 0 0 | * 1 * * * | 0 0 0 0 0 |
// | | 34|| | || 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 || 0 0 | 0 0 | 0 0 | 0 0 0 0 0 | * * 1 * * | 0 0 0 0 0 |
// | | 35|| | || 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 || 0 0 | 0 0 | 0 0 | 0 0 0 0 0 | * * * 1 * | 0 0 0 0 0 |
// | | 36|| | || _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ | _ _ | _ _ | _ 0 0 0 _ | * * * * 1 | _ 0 0 0 _ |
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+-----------+-----------+
// | 12 H| 37|| | || 0 0 1 | 0 1 0 | 0 _ _ | 1 0 0 | _ 0 _ | _ _ 0 | _ _ _ || 1 0 | 1 0 | 1 0 | _ 0 0 0 _ | _ 0 0 0 _ | 1 * * * * |
// | | 38|| | || 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 || 0 0 | 0 0 | 0 0 | 0 0 0 0 0 | 0 0 0 0 0 | * 1 * * * |
// | | 39|| | || 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 || 0 0 | 0 0 | 0 0 | 0 0 0 0 0 | 0 0 0 0 0 | * * 1 * * |
// | | 40|| | || 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 || 0 0 | 0 0 | 0 0 | 0 0 0 0 0 | 0 0 0 0 0 | * * * 1 * |
// | | 41|| | || _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ | _ _ _ || _ _ | _ _ | _ _ | _ 0 0 0 _ | _ 0 0 0 _ | * * * * 1 |
// +-----+----++---+----++-------+-------+-------+-------+-------+-------+-------++-----+-----+-----+-----------+-----------+-----------+
// |:info:| move point inside and press `C-u M-x satoku-mode RET'
As it turns out, neither s[7, 1] nor s[8, 1] can be selected at all. The only possible set of selections is { s[7, 0], s[8, 0], s[9, 0] }.
Note
Clause sub-matrix S6 never degrades to a 2-row clause sub-matrix, but the problem is still solved, since there are no conflicts left. I.e., it may or may not be necessary to degrade a satoku matrix to the representation of a 2-SAT instance.
Advantages
The satoku matrix shows, that the distinction between variables and clauses of a SAT problem is artificial without any real advantage.
It is the strong opinion of the author, that the willy-nilly distinction leads to willy-nilly decisions and therefore is even detrimental. But ... your mileage may vary.
|:todo:| advantages, explain
Obfuscated XOR Structure
It is also possible to detect obfuscated XOR-SAT instances and deobfuscate them properly.
|:todo:| obfuscated XOR structure, explain
Per-Problem Worst Case Upper Bound
|:todo:| per-problem worst case upper bound, explain
Summary
This structural system offers a rich environment of operations based on the algebraically boring single selection operator.
So next time you think you know it all, remember that this impression comes from your delusions of grandeur.
Mathematical Theories
There are mathematical and non-mathematical problems. Although computer science seems to ignore anything that does not have a defined mathematics attached, non-mathematical problems are by far more common for DOGgy style programmers than mathematical stuff.
Mathematically oriented programmers tend to create nicely structured problem models. It is usually perfectly fine to ignore anything that does not fit in the rigid context of axiomatic definitions (that is the purpose they were constructed for after all: exclude things, that the theory can't handle).
As long as the problem domain can be arbitrarily defined, constructing a mathematical model is a very good strategy.
However, clinging to mathematically consistent theories believing that they will eventually be the salvation for software development is also a variety of delusions of grandeur.
Paradoxes
Lemma: The limited use of mathematical models in DOGgy style programming is due to the fact that mathematics treats logic universally (without a time component) and ultimately excludes paradoxes from it's scope. However, DOGgy style has both completely paradoxical axioms and a prominent time component (the program will be finished real soon).
A famous example for a paradox is the Liar paradox:
Epimenides, the Cretan, spoke in truth when he said that everything that Cretans say is false.
Self-referential statements are good candidates for paradoxes. E.g., Russell's paradox, "The set of all sets that are not members of themselves".
The mathematical resolution is basically to ignore this[17], e.g., by showing that a "set of all sets not containing themselves" cannot exist (see Russellsche Antinomie (German)):
Based on: y ∈ x ↔ y ∉ y, x, y are arbitrary sets Substituting x for y, this renders a contradiction: x ∈ x ↔ x ∉ x, which is used to show that: ¬∃ x: ∀ y: y ∈ x ↔ y ∉ y
- There is no set of all sets having themselves not as an element.
- There is no set of all sets.
- These are classes, which are not sets.
Good. ZFC set theory is saved. We get a nice theory with lots of mathematical applications.
So, who needs sets containing themselves anyway? Well, DOGgy style programmers do, and if it's only for fun. One of the first things you find about sets having themselves as element, is that you already constructed your first endless loop in form of an unterminated exponential recursion:
A = { A, 1, 2 }
A' = { { A', 1, 2 }, 1, 2 }
A'' = { { { { A'', 1, 2 }, 1, 2 }, 1, 2 }, 1, 2 }
A''' = { { { { { { { { A''', 1, 2 }, 1, 2 }, 1, 2 }, 1, 2 }, 1, 2 }, 1, 2 }, 1, 2 }, 1, 2 }
...
Well, this is just naive set programming :). Using references instead of expanded sets avoids this problem:
r = Ref(R)
A = { a, 1, 2 }
Done. No more recursion during construction, only when fully expanding such a thing. And of course, you should never do that without the necessary precautions.
Here is a Perl(1) example using DATA::Dumper, that can deal with arbitrary self-referential data structures perfectly well:
use Data::Dumper;
my $hashes = [ {}, {}, {} ];
my $last = undef;
foreach my $hash ( @{$hashes} ) {
$hash->{'me'} = $hash;
$hash->{'prev'} = $last;
$last = $hash;
}
printf STDOUT ( "%s\n", Data::Dumper->Dump([$hashes], ['$hashes']) );
This program displays:
$hashes = [
{
'prev' => undef,
'me' => $hashes->[0]
},
{
'prev' => $hashes->[0],
'me' => $hashes->[1]
},
{
'prev' => $hashes->[1],
'me' => $hashes->[2]
}
];
Here is an example, which implements the contains-itself (CS)/does-not-contain-itself (NS) partition and a universal class:
- arbitrarily putting NS into CS, classifying NS as containing a reference to itself (despite all correct resolutions of Russell's paradox), however, NS does not actually contain itself,
- arbitrarily putting CS into NS, classifying CS as not containing a reference to itself,
- constructing the universal class from the union of CS and NS.
class Universe(dict):
def __repr__(self):
sets = [' '.join((k, repr(v))) for k, v in sorted(ditems(self))]
return '\n'.join(sets)
def __init__(self, *args, **kwargs):
super(Universe, self).__init__(self, *args, **kwargs)
self['CS'] = Set(['ns', 'v'])
self['NS'] = Set(['cs'])
def __getitem__(self, key):
if key == 'V':
V = self['CS'].union(self['NS'])
return V
return super(Universe, self).__getitem__(key)
def iteritems(self):
items = []
for k in self['V']:
name = k.upper()
items.append((name, self[name]))
return items
items = iteritems
def add(self, name, set_):
if not name:
return
if name in ('CS', 'NS', 'V'):
return
if name in self:
self[name] = self[name].union(set_)
else:
self[name] = set_
ref = name.lower()
if ref in set_:
self['CS'].add(ref)
else:
self['NS'].add(ref)
def parse(self, input_):
for line in input_.splitlines():
set_ = Set()
name = set_.parse(line)
V.add(name, set_)
class Set(set):
def __repr__(self):
return sformat('{{ {0} }}', ', '.join(sorted(self)))
def parse(self, line):
name = None
self.clear()
fields = line.strip().split(' ', 1)
while True:
if not fields:
break
name = fields.pop(0)
if not fields:
break
set_def = fields.pop(0).replace('{', '').replace('}', '').replace(',', '').strip()
self.update(Set(re.split('\\s+', set_def)))
break
return name
V = Universe()
V.parse(input_)
printe(V)
With the following input:
input_ = '''
A { a, b, c }
B { a, c }
C { d }
D { a, d }
'''
this output is produced:
A { a, b, c }
B { a, c }
C { d }
CS { a, d, ns, v }
D { a, d }
NS { b, c, cs }
V { a, b, c, cs, d, ns, v }
Feeding the output back in as input, produces a stable result.
Lemma: Mathematics is a two-edged sword. If you know the limitations of mathematical theories, it can help you avoid running into paradoxes like this and avoid the risk of endless loops and data corruption. But mathematics, like anybody else, does not like to talk about limitations so much. Your algorithm book probably does not mention these things, too. (They have a tendency to deal with nice mathematical stuff that works, not the gory fringe stuff that does not work).
Corollary: Your programming language knows nothing about mathematical theories. It gives you a data type called set, but it only faintly resembles a mathematical set. There are no provisions to protect you from the pitfalls, which have a tendency to show up only with customers.
Cybernetics is a nice approach to tackle paradoxes like the problem of future contingents.
A simple state machine (no triggers needed) for the "catalog of all catalags that do not list themselves" presents just another oscillator:
+-------+ remove c +-------+ | c ∈ c | ----------> | c ∉ c | | | <---------- | | +-------+ add c +-------+
So, depending on when you look, the catalog either lists itself or it does not. No contradiction necessary.
It's a little bit like Schrödinger's cat. (It's just a joke. I'm not serious!).
Here is the special flavor of delusions of grandeur regarding modeling:
All problems can be mapped to a rigid mathematical model.
I am on the safe side sticking to proven mathematics in a program.
Modal Logic
The modal fallacy.
See modal logic at Wikipedia.
Introduction to modal logic: Possible Worlds by Norman Swartz.
The basic unary (1-place) modal operators are usually written □ for Necessarily and ◇ for Possibly. In a classical modal logic, each can be expressed by the other with negation:
◇ P ↔ ~ □ ~ P□ P ↔ ~ ◇ ~ P
Thus it is possible that it will rain today if and only if it is not necessary that it will not rain today; and it is necessary that it will rain today if and only if it is not possible that it will not rain today.
Sloppy Algorithms
Isn't it funny, that the economically most successful software is based on the (intentionally) sloppiest manifestation of algorithms, I have ever seen? :) (I'm talking about MS).
List of Mathematical Symbols
| ⌈ ⌉ | ceiling |
| ⌊ ⌋ | floor |
| ∏ | product |
| ∑ | sum |
| ∃ | exists |
| ¬∃ | not exists |
| ∀ | for all |
| ¬ | negation |
| ∧ | and |
| ∨ | or |
| ⊻ | xor |
| ⊕ | xor |
| ⇒ | implication |
| → | if … then |
| ⇔ | material equivalence |
| ↔ | iff |
| ∈ | in |
| ∉ | not in |
| ∪ | union |
| ∩ | intersection |
| ~ | falsity | tilde |
| ◇ | possibility | diamond |
| □ | necessary truth | box |
| ∇ | contingency | nabla |
| Δ | necessary truth | delta |
| ⊢ | infer see propositional calculus |
The list of mathematical symbols might be helpful to find interpretations of symbols.
Non-Mathematical Problems
Mathematicians seem to be so used to declare things negligible, that they are prone to forget that some things can simply not be neglected. Just because a theory cannot handle something, does not make it go away when you ignore it.
Since non-mathematical problems of sufficient complexity are heterogeneous, i.e., structured and unstructured sub-problems are mixed, there will never be a single good strategy to solve them.
Insisting on systematic and fully structured models, along with the common fallacy of ignoring that the map is not the territory, some highly philosophical and aggressive discussions about certain non-concepts can be had:
Invalid use cases
Last time I checked, a use case could very well have illusionary requirements, which still does not make it invalid. A use case can also be hard to model, or a model can be a bad fit for a use case. Still, no invalidation in sight. Price too high? Not invalid.
False solutions
A problem can have an arbitrary amount of solutions. If a program does not solve a problem, it does not become false, it is just not a solution to the problem. If a program solves a problem, but does not fulfill the requirements of an arbitrary model, it is still a solution. It does not magically become false. What is the frame of reference?
Correct models
The correctness of a model is independent from a problem. It's a mathematical thing. A model can be fully correct, but still be a bad fit to a problem. On the other hand, there are models, which are not mathematically correct (in all regards), but still be a good fit for a problem.
Incorrect documentation
The documentation is an abstract model of the program it describes. Since the map is not the territory, all documentation is necessarily somewhat incorrect. Like models, documentation is a good or bad fit.
Necessary documentation
All documentation is necessarily incomplete. When is a necessity fulfilled? Certainly, when the documentation becomes the program itself.
Should the documentation be able to enlighten the reader? How about the daodejing, art of war, confucius, torah, bible, quran then?
Data Is Amorphous
Object Orientation (OO)
Let me state this clearly and firmly beforehand. I do like and want object oriented support in a programming language.
This section is meant to shine some light on the illusion that programming languages are somehow object oriented, and that there are programming languages which are not. OO is actually a matter of structure in the programmer's mind. It is not a feature of a programming language. Programming languages can have good or bad support for object oriented thought patterns. That's all.
The glorified Array
Assembler, C, C++ use glorified arrays to represent objects.
#include <stdio.h> #include <stdlib.h> #include <string.h>
A language supported object:
struct Obj {
long int id;
char *name;
long int age;
};
A glorified array:
#define OBJ_id_TYPE long int #define OBJ_id_OFS 0 #define OBJ_name_OFS (OBJ_id_OFS + sizeof(OBJ_id_TYPE)) #define OBJ_name_TYPE char * #define OBJ_age_OFS (OBJ_name_OFS + sizeof(OBJ_name_TYPE)) #define OBJ_age_TYPE long int #define OBJ_SIZEOF (OBJ_age_OFS + sizeof(OBJ_age_TYPE)) #define OBJ_DOT(obj, member) \ (*(OBJ_ ## member ## _TYPE *)((char *)(obj) + OBJ_ ## member ## _OFS))
Some visualization:
void hexdump(char *name, void *data, long int size) {
int indx;
printf("%s[%03ld]: ", name, size);
for ( indx=0; indx<size; ++indx ) {
printf("%02x", ((char *) data)[indx]);
}
printf("\n");
}
int main(int argc, char** argv) {
Allocate and fill an object with builtin OO support:
struct Obj obj; obj.id = 55; obj.name = "me"; obj.age = 53;
Allocate and fill an object with glorified array support:
char oraw[OBJ_SIZEOF]; OBJ_DOT(oraw, id) = 55; OBJ_DOT(oraw, name) = "me"; OBJ_DOT(oraw, age) = 53;
And now show some output:
{
int equal_error = memcmp(&obj, &oraw, sizeof(struct Obj));
printf("obj and oraw are%s equal\n", !equal_error ? "": " not");
if (equal_error || 1 == 1) {
hexdump("Obj", &obj, sizeof(struct Obj));
hexdump("OBJ", oraw, OBJ_SIZEOF);
}
exit(equal_error);
}
}
Output:
obj and oraw are equal Obj[024]: 370000000000000005084000000000003500000000000000 OBJ[024]: 370000000000000005084000000000003500000000000000
The glorified Hash
Lisp, Perl, Javascript, Python use a hash table or dictionary (or assoc list) to represent object. The principle is the same, but the implementation might be different.
Programming Techniques
Discipline
Lemma: Anything requiring discipline is subject to Murphy's Law.
Templates (Cut-and-Paste)
Lemma: Templates are good and necessary. Working without templates is unproductive.
A good template system does not require you to remember much and it does not require special formats.
Lemma: A template system should not force you to invent names. That is only a distraction from your current activity, and DOGgy style programmers will never choose an appropriate name at the first try.
Templates must be editable with your normal editor.
Placeholder are necessary, but filling them out should be optional wherever possible. Grep-able tags are good placeholders.
Tags serve several context dependent purposes:
- outlining (multi-level structure)
- bookmarks
- region markers
- reminders
Tagging
Is good. Correct tagging is better (see SORTME and TODO).
Adhoc (On-the-fly)
Lemma: Adhoc programming is unavoidable, since avoiding it would require Discipline.
SORTME and TODO
Lemma: Adhoc programming directly leads to SORTME and TODO tags, which are contradictory statements, since the intended sorting or elaboration is practically never done.
Consider creating a Snippet template, before applying a SORTME tag. A snippet template is easier to find than SORTME tags.
Use TODO only for things, that actually need to be done.
Use CHECK for things, that you actually do not intend to do, unless you absolutely must.
Documentation
Lemma: The major purpose of documentation is to have somthing to complain about as long as it's missing. Normal people will not read your documentation.
Since DOGgy style programs cannot be easily understood by mathematically trained computer scientists, no amount of documentation will enhance the understanding of the mixture of convential, strange and outright false concepts.
So document only, what you need for your own purposes. You must be able to get back on track when you try to extend an old project. And you must be able to re-use the code in other projects. That's it.
Doing this, will also show other people, what you really consider important. If someone else has different opinions about importance, they can extend the documentation accordingly.
Template Languages
Inline template languages like PHP and Mako are almost evil, since they support a style of adhoc programming that leads to unmaintainable code. Since it requires a lot of Discipline to avoid the pitfalls, they are hard to use.
Documentation languages are good, since they are confined to comments and strings.
Snippets provides an inline template language, where template control structures are block oriented, strictly confined to comments, and template expansion in verbatim template text is atomic.
Unit Tests
Unit tests are absolutely necessary. (See also Confessions of a Terrible Programmer).
However, resist the temptation to use convoluted test environments which make your life easier. They don't, if you don't carry them around.
Polymorphism effiency dictates, that you write your unit tests in such a manner, that they can also serve as usage examples, aka. snippets.
Libraries
Version Dilemma (DLL Hell)
Libraries are basically a good thing. However, a combinatory explosion of effort can happen, if libraries are not available in different versions.
Although you may enjoy the sensation of a good explosion, as DOGgy style programmer, you probably dislike unnecessary effort more.
If a library becomes incompatible to previous versions, they require update efforts proportional to their use.
Lemma: Good DOGgy style programming makes sure, that libraries can always be included locally to a project, to avoid the necessity of update efforts. I.e., always carry them around in case you need them. But do not use them unless necessary!
This is counter-intuitive to a library's intended purpose of code re-use, but it ensures, that libraries and operating systems can be upgraded willy-nilly by administrators (who always schedule their upgrades at inconvenient times, and they never give you root privileges, see also Bastard Operator From Hell).
IDE
So there are editors, IDEs and Emacs.
Notepad is an editor. Eclipse is an IDE. Emacs is a programming language, which -- among other things -- happens to be an editor and an IDE.
IDEs generally suffer from delusions of grandeur of their programmers. They try to predict any conceivable use case.
Installation Time
How long does it take you to set up your development environment on a fresh machine?
It must have your editor and templating system. So for me that is Emacs, my Emacs packages and Snippets. So it takes me 15-30 minutes.
How about you Eclipse guys? Does it even ever run, or do you need someone from IT-administration?
File-Local IDE Features
C-x C-e in Emacs allows for adhoc lisp code to be executed in any buffer.
Since adhoc lisp code can invoke functions, macros, shell-commands, compilation and actually everything else you can do in emacs, it is perfectly suited to provide for file-local IDE features.
Dynamic abbreviations vs. Intellisense
Here is a discussion of intellisense and its inherent problems: Why PHP and JavaScript IDE's Suck. So I will not go into that.
Computers are not intelligent. Computers are very well suited to store huge amounts of information accurately. But that has nothing to do with intelligence. An idiot savant can do that.
Programming languages are very simple and also not intelligent. Determining the basic context in a programming language is a very simple task. So there is not much intelligence necessary to implement intellisense.
However, determining the intented context of a programmers action is an impossible task. And not only in an algorithmic sense or due to run-time requirements.
Consider this example:
variable = MyClass() variable.
For intellisense, typing the dot must mean, that a member of MyClass is accessed, right?
Wrong. I am intending to introduce a member, which has not been defined yet. And I do not wish to define it now (in Python or Javascript it is not even necessary), so I don't loose my train of thought. The compiler will tell me later, that I have not yet defined the member. And I will then fix it, or maybe not. It really depends on, whether I am in the right mood.
But intellisense insists on being right and pops up a list of known members, which is distracting and annoying, since I already know, that the accessed member cannot be in that list yet.
Dynamic abbreviations on the other hand are humble. They do not assume anything but the barest facts. You start to type a word, hit a key, and it tries to complete it. It applies some uppercasing/lowercasing as it sees fit (which is more often correct than incorrect). But that's it. However, it can even complete entire sentences skipping over punctuation as necessary.
It could be argued, that a list of known members is not entirely useless when defining a new member, since it shows, what names cannot be used anymore. But dynamic abbreviations can do that too. A simple grep can do that, if necessary.
The copyright notice of dabbrev.el states:
;; Copyright (C) 1985, 1986, 1992, 1994, 1996, 1997, 2000, 2001, 2002, ;; 2003, 2004, 2005, 2006, 2007, 2008, 2009, 2010, 2011, 2012 ;; Free Software Foundation, Inc.
So, why in almost 30 years, has this feature not been implemented in each and every editor known to mankind?
For dynamic abbreviations to work well, it is necessary for the editor to keep track of the usage timeline of buffers. Emacs does that. Everybody else does not. So it's basically a design flaw, when an editor does not implement dynamic abbreviations, or can only implement them inefficiently.
So, why is a flawed program calling a simple feature intellisense. For me it is neither intelligent, nor does it make any sense.
Here is a Hacker News excerpt from Y Combinator in reference to Why PHP and JavaScript IDE's Suck:
jrockway
Dynamic abbreviations ("dabbrev-expand" and "dabbrev-completion") solve the problem quite nicely 90% of the time. If you keep the documentation open in another buffer, then it works 99% of the time, as long as you have a clue on what you're doing.
People seem a little bit too concerned about getting a java-style 100% correct solution when a 90% solution is nearly as good.
baha_man
I love Emacs, but I think the lack of 'Intellisense' is one of the few good reasons to use an IDE over Emacs or Vim. Some people think Intellisense rots the brain, but I can't see anyone ever saying that about eldoc-mode.
jrockway
lisp-complete-symbol definitely does rob the brain. I've written plenty of braindead Lisp with its help :) Eldoc is not the same thing, though, since it just shows some basic documentation after you've remembered the name of the function. It's a nice "yeah, I knew that was the name" reminder. Finally, it's easy to "dive deeper" with Lisp, thanks to "describe-function" and friends. I would definitely not complain about having that for other languages. (Languages that don't have docstrings are really annoying me these days. Perl especially.)
Honestly, I use dabbrevs more often than lisp-complete-symbol when writing lisp. It usually gets me what I want with less typing. (There are a lot of lisp functions that start with the same prefix, but not as many that I've used in my editor session. So dabbrev-expand has less to look at, and hence it usually gives me what I want faster.)
Expert Systems
The so-called expert systems are based on Horn-Clauses, which become utterly useless when solving 3-SAT.
Expert system:
[ 1 1 1 - - - - - - ] [ - - - 1 1 1 - - - ] [ - - - - - - 1 1 1 ] [ 0 - - - - - 0 - - ] [ - 0 - - - - - 0 - ] [ - - 0 - - - - - 0 ] [ - - - 0 - - 0 - - ]Teilen
Footnotes
| [2] | German readers might get some fun out of Oskar Panizza's novel Aus dem Tagebuch eines Hundes (PDF). |
| [3] | My actual feelings could be expressed like this: Sometimes I wish I was a mathematician
and see the world as comprehensible.
Sometimes I wish I was a logician
and see the world full of potential.
And then I find I'm neither -- just a measly DSP --
and nothing makes any sense at all.
|
| [4] | Without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE |
| [5] | Is that why single selection is not mentioned in my propositional calculus textbook? |
| [6] | I found that other people tend to share this misconception, making it hard to explain the difference between selecting a literal and assigning a truth value to a variable. Obviously a selection does not entail that all variables of the same kind must also be selected. |
| [7] | ... or combinations or variations -- I will look that up for the umpteenth time, as soon as I feel like it |
| [8] | When I was playing Schafkopf (a German card game), I used to play with utmost sincerity to the very end. This used to elicit the remark "wir sind doch schon zu!" ("we have already closed", i.e., "we have already won") from more experienced players. They were wondering, why I was still deliberating what to do, expressing the fact that no matter what I would do, it would not no longer have any influence on the outcome of the game. Well, it's simple: I did not have the faintest idea what the prospect of winning or loosing the game was, since I did not track the amount of points won by either party. |
| [9] | BTW: This principle is often used in digital electronic data sheets, where the required voltage level at an input is denoted as NC (no care), if the actual voltage level does not have any influence on the operation of the chip. Nobody ever demands, that the manufacturer must fill in a "real" value. Not even in the USA, where it is perfectly possible, that electronic datasheet must have a sticker: "Warning: The NC values in this datasheet can damage your mind". |
| [10] | I think I know now. I have forgotten, that truth tables are the holy representation of logic. And a correct truth table does not contain anything but True and False. To find out, whether a truth value assignment is a solution to a problem, it is necessary to assign a truth value to all variables. Otherwise, the solution cannot be looked up in the truth table.
Lemma: The customer is always right. If the customer wants it that way, you give it to him that way. Period. On the other hand: This is not Burger King, you either take it my way, or you don't get it. |
| [11] | OK! That is, why single selection is not in my propositional calculus textbook. |
| [12] | Since my mathematical skills and knowledge are too limited, I spent a long time re-inventing the wheel, such as proving (inductively starting with truth tables, because that's the only thing I know) on some 100 odd pages that my mapping operation is correct. Just to find that I had not even started to talk about the actual subject. And then - by accident - I found the exact same mapping being used to reduce the independent set problem to 3-SAT. So it turned out, that everything I proved was already common knowledge (it's just too hilarious ;-)). The way I expressed it was simply way too off-site for the general mathematical consensus. Although completely unnecessary, I would still not say, that my attempt at a proof was a waste of time, as it does have other merits in itself. I now find myself proving things to myself to get a good grip on a concept. When I gave the proof to my cousin (a mathematician), she started reading and after while, she asked me, whether this could be an inductive proof. When I said "yes of course", she sighed and that was the end of the story. It took me a while, but now I know why that is so. I would like to thank professor Mount again for making his lecture notes available, so I could rise from my dark corner of the universe into the bright light. |
| [13] | David M. Mount, CMSC 451 Lecture Notes, Fall 2012 (local copy) with kind permission from the author, should the document no longer be availabe at the original location. |
| [14] | This violates the requirements of a well formed 3-SAT problem in conjunctive normal form. So, strictly speaking, we are no longer dealing with a 3-SAT problem. Chances are, that this will be pointed out and the entire algorithm will be dismissed. It is a good example, how clinging to the model instead of following the problem can lead to (virtual) conflicts. |
| [15] | OK, I could not resist. If you want a 3-SAT CNF, you can proceed further ... The 2-literal clause vectors are now extended to 3 values, by duplicating them and adding a new variable to each instance (once negated and once unnegated): [ 1 1 1 - - - - - - ] [ - - - 1 1 1 - - - ] [ 0 - - 0 - - 0 - - ] [ 0 - - 0 - - 1 - - ] [ - 0 - - 0 - - 0 - ] [ - 0 - - 0 - - 1 - ] [ - - 0 - - 0 - - 0 ] [ - - 0 - - 0 - - 1 ] s s s s s s c c c 0 0 0 1 1 1 0 1 2 0 1 2 0 1 2 The clause vectors can then be translated to a 3-SAT problem in conjunctive normal form: ( s00 ∨ s01 ∨ s02) ∧ ( s10 ∨ s11 ∨ s12) ∧ (¬s00 ∨ ¬s10 ∨ ¬c0 ) ∧ (¬s00 ∨ ¬s10 ∨ c0 ) ∧ (¬s01 ∨ ¬s11 ∨ ¬c1 ) ∧ (¬s01 ∨ ¬s11 ∨ c1 ) ∧ (¬s02 ∨ ¬s12 ∨ ¬c2 ) ∧ (¬s02 ∨ ¬s12 ∨ c2 ) |
| [16] | Isn't it beautiful, how avoiding decisions can provide tons of information ;-). |
| [17] | Since we do want to have prime numbers at least, self-referential statements cannot be excluded as a general rule. |
References
| [PW] | Possible Worlds (internet), Possible Worlds |
| [ML] | modal logic |
| [someone] | Someone, F. Sure, Something, Somewhere Sometime |
Copyright
Copyright (C) 2013, Wolfgang Scherer, <Wolfgang.Scherer@gmx.de>. See the document source for conditions of use under the GNU Free Documentation License.