Rationale for the Satoku Matrix
| Author: | Wolfgang Scherer |
|---|
Contents
- All CNF Satisfiability Problems Can Be Made Worse
- The Structure of Regular XORSAT Problems Can Be Recovered Efficiently
- Analyzing The Conflict Structure of SAT Problems Gives Strict Upper Bounds For Complexity
- There Is No Difference Between Clauses And Variables
- Solving Strategies
- Structural Decomposition of Regular XORSAT
- Full Logs of SAT-Solver Experiment
The question is: Is it worth the effort to document the satoku matrix formally[1]?
The answer to that question is "yes", if:
1.1) At least one of the following conclusions is new.
- 1.2) The conclusions do not contradict any established mathematical or
- logical principles.
If any of the conclusions is invalid or old news, I would be highly interested to know about it, because it makes my task easier.
If I use the incorrect terms to describe a principle, I would also be highly thankful to learn about it, because it also makes my task easier.
I marked assumptions that I make, which I am not 100% certain about.
What I know so far is that
- Graph theory is necessary but not sufficient to express the satoku matrix algorithms.
- Propositional logic is necessary and sufficient but lacks expressiveness.
- Decision algorithms are a true subset of the satoku matrix.
- A formal proof requires nothing but basic propositional logic.
Note
The class of regular XORSAT problems was only choosen for its symmetric properties. The analysis applies to all SAT problems equally.
All CNF Satisfiability Problems Can Be Made Worse
Observation: The running time of variable based decision algorithms varies significantly for 3-regular bipartite graphs depending on whether the problem is encoded as regular XORSAT problem or whether it is encoded as the corresponding independent set problem.
There is a difference in actual running times for the same problem between 32s, 227612s and indefinite (>777881s) (MiniSat).
Example: Feed three differently encoded versions of the same problem mod2-3cage-unsat-9-10.cnf, into a SAT-Solver and watch the effects on running time. (I used MiniSAT v1.14, CryptoMiniSat 2 v2.9.8 and lingeling/treengeling ats 57807c8f410a9e676816984a0ad0c410e485bcae)
- Case 1 is the original problem.
- Case 2 is the result from stage 1 of the satoku matrix encoded as independent set problem. It adds some additional conflicts and removes redundancies to support a decision algorithm, but uses worst case encoding.
- Case 3 is the unmodified encoding of the independent set problem.
Running times of SAT solver MiniSAT:
| Variation | Running Time | Solved | Comment |
|---|---|---|---|
| Case 1 | 32s | yes | which was expected |
| Case 2 | 22761s | yes | this makes the results strange at first glance |
| Case 3 | 777881s | no | which was expected |
Running times of SAT solver CryptoMiniSat:
| Variation | Running Time | Solved | Comment |
|---|---|---|---|
| Case 1 | 0.85s | yes | which was expected, since it has XOR support |
| Case 2 | 73616s | no | this is strange, no solution after 20 hours, although MiniSAT only took 6 hours |
| Case 3 | 73430s | no | which was expected |
The problem is based on a 3-regular bipartite graph, so the structure is well-known (regular XORSAT):
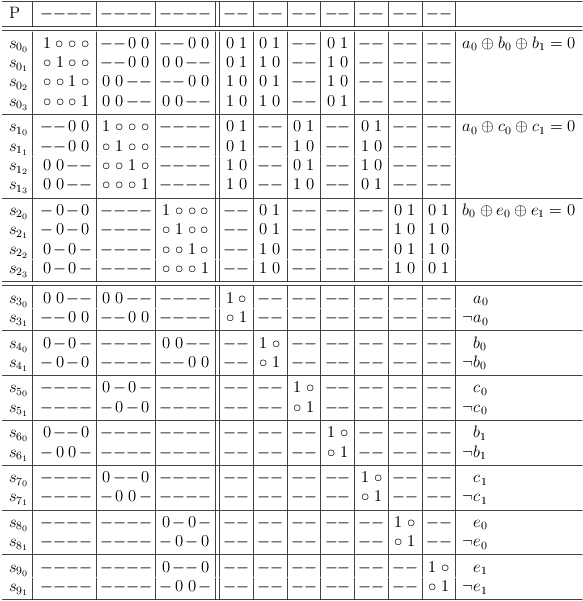
Structural analysis of regular XORSAT
For further details see Structural Decomposition of Regular XORSAT.
Note
This example was chosen for fireworks effect. The results do not depend on the structure of the problem. They can be seen with arbitrary CNF-problems.
But They Can Also Be Made Better
All three versions for the experiment are invariant in the context of the satoku matrix. I.e., the hardness of the problem is identical, although the input size measured in total number of variables and 2-literal clauses varies significantly. However, the number of k-literal clauses, k ≥ 3 is constant. (Oops, case 2 has m/2 due to redundanc eliminiation. I will fix that later).
Case 1 is also isomorphic to case 3. After stage 1 of the satoku matrix algorithm, all three cases become isomorphic.
The original structure can be discovered efficiently and the XORSAT encoding can be restored.
Experiment
The dimacs files used are:
- mod2-3cage-unsat-9-10.cnf
- mod2-3cage-unsat-9-10-vertex-cover-with-conflicts.cnf
- mod2-3cage-unsat-9-10-vertex-cover-with-conflicts-red-elim.cnf
- mod2-3cage-unsat-9-10-vertex-cover-without-conflicts.cnf
Analysis with the satoku matrix makes the following predictions for n-complexity (based on number of variables) and m-complexity (based on number of clauses) for the original problem:
n-complexity: 229m-complexity: 229
Since 2-literal clauses can be ignored after construction of the satoku matrix, m-complexity is expected to be constant at 229 .
lingeling/treengeling are a class of their own.
The most interesting result is case 2, where MiniSat outruns CryptoMiniSat in time (but not in the number of decisions).
Feed the original problem:
87 variables232 clauses696 literalsinto the SAT-Solver:
$ lingeling mod2-3cage-unsat-9-10.cnf c Lingeling SAT Solver c Version ats 57807c8f410a9e676816984a0ad0c410e485bcae s UNSATISFIABLE c 33531 decisions, 204827.0 decisions/sec c 0.2 seconds, 1.9 MB
Very good.
c Treengeling Cube and Conquer SAT Solver c Version ats 57807c8f410a9e676816984a0ad0c410e485bcae s UNSATISFIABLE c 0.03 wall clock time, 0.03 process time c 9417 decisions, 282623 decisions per second Extremely good.
$ MiniSat_v1.14_linux mod2-3cage-unsat-9-10.cnf
restarts : 26
decisions : 9885877 (308144 /sec)
CPU time : 32.082 s
UNSATISFIABLE
The number of decisions for MiniSat v1.14 is between :math:`2^{23}` and
:math:`2^24`. This is consistent with the observation, that
unsatisfiability of a real XORSAT problem is ususally detected when
there are still about 12 clauses left (4-SAT). Since each decision
removes 2 clauses, this results in effective savings of 6
decisions. Hence :math:`2^{(29-6)} = 2^{23}`.
$ cryptominisatLinux64 mod2-3cage-unsat-9-10.cnf
c Finding non-binary XORs: 0.00 s (found: 32, avg size: 3.8)
c restarts : 38
c decisions : 197651 (0.85 % random)
c CPU time : 0.85 s
s UNSATISFIABLE
CryptoMiniSat only needs between :math:`2^{17}` and :math:`2^{18}`
decisions (probably Gauss-Jordan).
$ MiniSat_v2.2.0 mod2-3cage-unsat-9-10.cnf restarts : 65535 decisions : 76108189 (0.00 % random) (585108 /sec) CPU time : 130.075 s UNSATISFIABLE MiniSat v2.2.0 (simp) needs between :math:`2^26` and :math:`2^27` decisions.
Apply the satoku matrix conflict bias to the problem, remove redundant clauses, convert it to a simple selection problem with conflict bias:
696 variables6688 clauses13608 literalsand to a simple selection problem with conflict bias and redundancy removal:
348 variables1730 clauses3576 literalsand feed it into the SAT-Solver:
$ lingeling mod2-3cage-unsat-9-10-vertex-cover-with-conflicts.cnf c Lingeling SAT Solver c Version ats 57807c8f410a9e676816984a0ad0c410e485bcae c 8647016 decisions, 68950.9 decisions/sec c 125.4 seconds, 16.3 MB $ lingeling mod2-3cage-unsat-9-10-vertex-cover-with-conflicts-red-elim.cnf c Lingeling SAT Solver c Version ats 57807c8f410a9e676816984a0ad0c410e485bcae c 9647858 decisions, 72686.7 decisions/sec c 132.7 seconds, 18.1 MB
Number of decisions between 223 and 224 . So the XOR-structure is detected properly. Why the reduced problem needs more decisions is beyond my imagination (random stuff?).
$ treengeling mod2-3cage-unsat-9-10-vertex-cover-with-conflicts.cnf c Treengeling Cube and Conquer SAT Solver c Version ats 57807c8f410a9e676816984a0ad0c410e485bcae s UNSATISFIABLE c 18130940 decisions, 207242 decisions per second $ treengeling mod2-3cage-unsat-9-10-vertex-cover-with-conflicts-red-elim.cnf c Treengeling Cube and Conquer SAT Solver c Version ats 57807c8f410a9e676816984a0ad0c410e485bcae s UNSATISFIABLE c 20269340 decisions, 211620 decisions per second Number of decisions between :math:`2^24` and :math:`2^26`. So the XOR-structure is detected properly. (different number of decisions?)
$ MiniSat_v1.14_linux mod2-3cage-unsat-9-10-vertec-cover-with-conflicts-red-elim.cnf restarts : 37 decisions : 523453042 (22998 /sec) CPU time : 22761.1 s UNSATISFIABLE The number of decisions for MiniSat is almost :math:`2^29`. This is consistent with the observation that the most suitable variables for the encoding affect 4 clauses for one assignment and only a single clause for the complementary assignment. It is therefore harder to detect unsatisfiablity.
$ cryptominisatLinux64 mod2-3cage-unsat-9-10-vertex-cover-with-conflicts-red-elim.cnf *** INTERRUPTED *** c restarts : 415 c decisions : 90622941 (0.10 % random) c CPU time : 73616.17 s CryptoMiniSat is a lot slower. I have no idea why.
Convert the original problem to a simple selection problem without conflict bias:
696 variables2320 clauses4872 literalsand feed it to the SAT-Solver:
$ lingeling mod2-3cage-unsat-9-10-vertex-cover-without-conflicts.cnf c Lingeling SAT Solver c Version ats 57807c8f410a9e676816984a0ad0c410e485bcae c c seconds irredundant redundant clauses agility height c variables clauses conflicts large ternary binary glue MB c c S 0.0 696 2320 0 0 0 0 0 0.0 0.0 0 c S 1.0 464 1392 27799 4009 304 117 34 18.5 37.4 2 c P 2.0 464 1392 60204 5646 408 117 34 20.3 35.0 1 c P 5.0 464 1392 140205 10112 588 131 33 21.7 33.3 1 c S 10.0 464 1392 260130 18148 760 131 32 22.8 36.1 5 c S 20.1 464 1392 446840 29573 902 131 36 24.6 35.8 8 c S 30.0 464 1392 688412 17527 975 131 36 24.9 34.9 3 c S 40.0 464 1392 880593 29760 1023 131 34 25.1 34.2 8 c S 50.0 464 1392 1112193 24998 1073 131 35 25.1 33.6 6 c S 60.0 464 1392 1301436 31551 1099 131 34 25.1 33.1 6 c S 120.0 464 1392 2547965 10803 1194 131 35 24.9 31.7 2 c S 180.0 464 1392 3824238 44801 1313 131 33 23.9 30.4 16 c S 240.0 464 1392 4820001 44862 1389 131 35 22.8 29.9 12 c S 300.1 464 1392 5498966 78208 1471 131 33 22.7 29.9 20 c S 600.1 464 1392 8209890 77636 1568 131 30 22.6 29.7 31 c S 900.0 464 1392 13119364 49052 1725 131 33 22.0 28.6 17 c S 1800.1 464 1392 22958750 98750 1846 131 34 20.9 27.8 47 c S 2700.0 464 1392 29859729 232033 1865 131 33 20.6 28.1 85 c S 3600.1 464 1392 39400947 80448 1914 131 34 20.2 27.8 27 c S 4500.1 464 1392 49381455 66009 1967 131 34 20.2 27.8 24 c S 5400.1 464 1392 56661440 156566 1989 131 34 20.2 27.7 63 c S 6300.3 464 1392 61936487 211346 2010 131 33 20.3 27.6 44 c S 7200.1 464 1392 68721909 55905 2015 131 33 20.2 27.2 14 c c seconds irredundant redundant clauses agility height c variables clauses conflicts large ternary binary glue MB c c S 10800.1 464 1392 89996521 174065 2044 131 34 20.0 26.7 77 c S 14400.2 464 1392 104510218 378905 2059 131 34 20.1 26.5 99 c S 18000.3 464 1392 117971974 435974 2063 131 32 20.0 26.2 134 c S 21600.0 464 1392 130310650 383997 2065 131 34 20.1 26.2 115 c S 25200.1 464 1392 160551060 155962 2075 131 31 20.0 26.3 63 c S 28800.0 464 1392 192551073 95808 2076 131 31 19.9 26.2 28 c S 32400.1 464 1392 213821405 113555 2076 131 33 20.0 26.5 52 c S 36000.1 464 1392 229422256 242874 2076 131 32 20.0 26.5 96 **INTERRUPTED**
$ MiniSat_v1.14_linux mod2-3cage-unsat-9-10-vertec-cover-without-conflicts.cnf *** INTERRUPTED *** restarts : 43 decisions : 12838157330 (16504 /sec) CPU time : 777881 s The number of decisions for MiniSat is between :math:`2^33` and :math:`2^34`, which is consistent with the observation that for this encoding the most suitable variables only affect a single clause for both alternatives of an assignment. The predicted n-complexity in this case is :math:`2^58`.
$ cryptominisatLinux64 mod2-3cage-unsat-9-10-vertex-cover-without-conflicts.cnf *** INTERRUPTED *** c restarts : 163482 c decisions : 211788006 (0.15 % random) c CPU time : 73430.12 s I do not expect CryptoMiniSat to solve the problem faster. Therefore I did not let it run 9 days.
Verify Original Input (Case 1)
If you do not want to take my word for it, you can simply download the original problem from the archive hjkn-mod2-benchmarks.tar.gz on the web site Matti Järvisalo - SAT Benchmarks.
Roll Your Own (Case 3)
The input for case 3) encodes the original as independent set problem. It can be generated in this manner:
Start with an empty mapped problem.
For each clause of the original problem:
(a ∨ b ∨ ¬c) ∧ (a ∨ ¬b ∨ c)
assign a new variable to each literal and add a clause to the mapped problem containing the unnegated variables as literals (vertex set of independent set problem, "select at least one literal from each clause"):
(c0 ∨ c1 ∨ c2) ∧ (c3 ∨ c4 ∨ c5)
For each clause in the mapped problem add the necessary 2-SAT clauses to ensure, that only one literal can be selected (edges of independent set problem, inverted vertex cover problem):
(¬c0 ∨ ¬c1) (¬c0 ∨ ¬c2) (¬c1 ∨ ¬c2) (¬c3 ∨ ¬c4) (¬c3 ∨ ¬c5) (¬c4 ∨ ¬c5)
For each literal in a clause of the original problem that conflicts with a literal from a different clause, add a 2-SAT clause, that excludes selection of the conflicting literals (edges of independent set problem, inverted vertex cover problem):
(¬c1 ∨ ¬c4) (¬c2 ∨ ¬c5)
Principle of Case 2
The input for case 2) is a little bit more complex, and it's really better to just take my word for its correctness, unless you wish to dive into the satoku matrix right away.
The principle is:
Map each clause of the original problem:
(a ∨ b ∨ ¬c), (a ∨ ¬b ∨ c)
to a biased DNF (making the possible selections more specific but still equivalent, not only equisatisfiable):
(a ∨ (¬a ∧ b) ∨ (¬a ∧ ¬b ∧ ¬c)), (a ∨ (¬a ∧ ¬b) ∨ (¬a ∧ b ∧ c))
Remove redundant clauses by following the logical consequences (I have no idea how to do that without the satoku matrix, so you can just keep them, it really does not matter).
Map the result to the vertex cover problem corresponding to the independent set problem as explained above. It should be clear how to determine, whether two conjunctions represent conflicting selections or not.
Exponential Attack
A selection problem can again be encoded as independent set problem, and therefore the number of variables increases even more. The actual hardness of the problem stays the same, but a decision algorithm does not know anything about it. It never realizes, that it solves the same problem over and over.
This is a simple way to make problems appear harder than they actually are.
The Structure of Regular XORSAT Problems Can Be Recovered Efficiently
This is a special case, where the satoku matrix can recover the XOR structure of the problem very efficiently from the independent set encoding. I.e., the original variable set can be discovered.
One insight I gained from the satoku matrix was: structure cannot be destroyed, just diluted beyond recognition. Logic is really a funny animal.
For Other Types of Problems, The Mileage Varies, But Is Generally Good
It is generally possible to recover structural information from problems encoded as independent set problems efficiently.
In fact, the maximal structural ambiguity of the independent set 2-literal conflict clauses (inverted vertex-cover problem) is necessary to recover the structure. The principle being: First dilute maximally, then distill in clever ways.
It is even possible to recover an independent set problem from a pure encoding as vertex cover problem (2-SAT). Although, in that case I have no clue how efficient (yet).
Except For Hirsch Type Multi-Variable XORS
These are interwoven multi-variable selectors. There is no conflict maximization possible. They can be flattened, but that does not really help.
Analyzing The Conflict Structure of SAT Problems Gives Strict Upper Bounds For Complexity
The hardness of a problem is strictly defined by m-complexity. The input size is based on number and size of clauses. The absolute worst case upper bound for m-complexity is ceil(k ⁄ 2)m . It is not km .
Analysis of conflict structure and simple transformations based on amortized distributive expansion (only expand, if it strictly reduces overall complexity) reveal the structure of problems and can be used to efficiently deduce suitable variable subsets for decision algorithms.
There Is No Difference Between Clauses And Variables
There is no substantial difference between a traditional selection problem (independent set problem) and a decision problem. In the context of the satoku matrix, a decision algorithm simply confines the possible selections to the variable clauses. A traditional selection problem confines the possible selections to the mapped CNF clauses.
Assumption: The definition "select at least one literal from a clause" seems to lead to a semantic confusion what a selection from a clause and what a decision over a set of variables are.
Making a selection from a clause does not mean that any of the selections in other clauses referencing the same variable are ever made.
The mapping of a propositional formula to an independent set problem from above (Roll Your Own (Case 3)) shows exactly, what "at least one" and "exactly one" stand for.
The correct definition is "select exactly one literal from a clause".
There Are No Atomic Variables In k-SAT CNF Clauses, k > 1
Atomic variables only appear in 1-SAT clauses. Since 1-SAT problems cannot have conflicts without becoming unsatisfiable, all variables are atomic. However, they are also fully determined. I.e., there is no room for any decisions to be made. All selections from the clauses are possible and required:
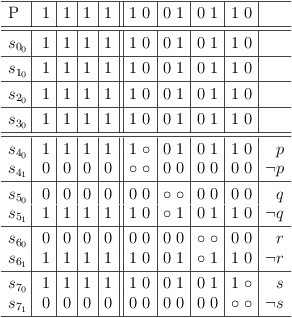
1-SAT example
CNF Is An Abstraction
A CNF formula with clauses of length k, k > 1 is an abstraction or representant of a set of conjunctions of DNF formulas D, where |D| > 1 .
CNF:
(a ∨ b ∨ c)
Set of DNFs D (list is not complete!):
((a ) ∨ ( b ) ∨ ( c)) ((a ) ∨ ( b ) ∨ (¬a ∧ c)) ((a ) ∨ ( b ) ∨ (¬a ∧ ¬b ∧ c)) ((a ) ∨ ( b ) ∨ ( ¬b ∧ c)) ((a ) ∨ (¬a ∧ b ) ∨ ( c)) ((a ) ∨ (¬a ∧ b ∧ ¬c) ∨ ( c)) ((a ) ∨ ( b ∧ ¬c) ∨ ( c)) ((a ∧ ¬b ) ∨ ( b ) ∨ ( c)) ((a ∧ ¬b ∧ ¬c) ∨ ( b ) ∨ ( c)) ((a ∧ ¬c) ∨ ( b ) ∨ ( c)) ((a ) ∨ (¬a ∧ b ) ∨ (¬a ∧ ¬b ∧ c)) ((a ) ∨ (¬a ∧ b ∧ ¬c) ∨ (¬a ∧ c)) ((a ∧ ¬b ) ∨ ( b ) ∨ (¬a ∧ ¬b ∧ c)) ((a ∧ ¬b ∧ ¬c) ∨ ( b ) ∨ ( ¬b ∧ c)) ((a ∧ ¬c) ∨ (¬a ∧ b ∧ ¬c) ∨ ( c)) ((a ∧ ¬b ∧ ¬c) ∨ ( b ∧ ¬c) ∨ ( c))
(I have a truth table somewhere, which proves the equivalence). |:todo:| (I know, that I did not catch them all). |:todo:|
Trivially, a 1-literal CNF clause is the representant of a single element set of DNFs.
CNF:
(a)
Set of DNFs D:
((a))
Remember that clauses of the form (p∨¬p) are not allowed in CNFs? Good, because it makes it easier to define the set of DNFs for variables being the special case of a 2-literal disjunction, where the set of DNFs for each literal is actually a single element. (This is really the only thing "special" about a variable).
Variable clause:
(p ∨ ¬p)
Set of DNFs D for a variable clause:
((p) ∨ (¬p))
It is really not so special, since the biased expansions of a variable would be:
(( p) ∨ ( ¬p ∧ ¬p)) ((¬¬p ∧ p) ∨ ( ¬p))
which is trivially equivalent to:
((p) ∨ (¬p))
General SAT Problem
A general SAT Problem can now be defined as normal CNF SAT-problem with the optional addition of a 2-literal variable clause for each of the variables:
(a ∨ b ∨ c) ∧ (¬a ∨ ¬b ∨ ¬c) ∧ (¬a ∨ ¬b ∨ c) ∧ (a ∨ ¬a) ∧ (b ∨ ¬b) ∧ (c ∨ ¬c)
Optional means, that the variables can be removed arbitrarily without incfluence on the final set of solutions. It also means, that variables can be ignored for sub-algorithms that determine the solving state. (What can be ignored and removed is a whole new can of worms, but very managable and easily provable).
When mapping to a satoku matrix, clauses can be replaced by any representant from the set of DNFs. (It can be done as a pre-mapping step also).
The mapping to a satoku matrix handles variables specially, in that each alternative conjunction of a variable clause is extended across the entire formula (this is not strictly necessary, but it avoids superfluous redundancies):
(c0 ∨ c1 ∨ c2) ∧ (c3 ∨ c4 ∨ c5) ∧ (c6 ∨ c7 ∨ c8) ∧ ((¬c3 ∧ ¬c6) ∨ (¬c0)) ∧ ((¬c4 ∧ ¬c7) ∨ (¬c1)) ∧ ((¬c5) ∨ (¬c2 ∧ ¬c8))
Example satoku matrix with plain variable clauses:
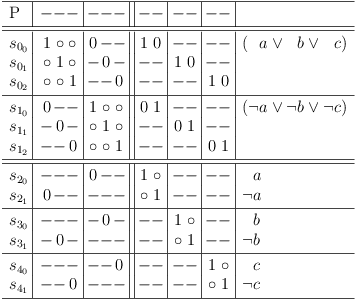
Satoku matrix with plain variable clauses
Example satoku matrix with conjunctive bias clauses:
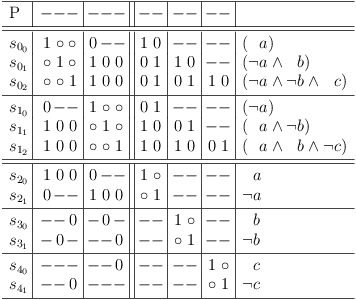
Satoku matrix with conjunctive literal clauses
Hopefully, this example shows, that variable clauses are indistinguishable from CNF clauses. They look like clauses, smell like clauses and squirm like clauses:
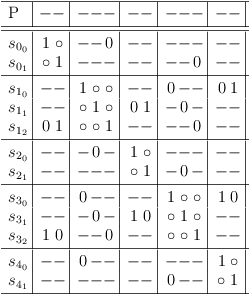
Variable clauses are indistinguishable from CNF clauses
Further Generalization
The mapping to a satoku matrix can handle any type of conjunctions of DNFs. There is no need to confine them to CNFs and their representants.
Amortized Distributive Expansion
Amortized means, that distributive expansion is only performed, if it actually reduces problem complexity.
The consequences of mapping different representants for the clauses can be seen, when performing amortized distributive expansion.
Amortized distributive expansion for reduced complexity, plain variable clauses:

Distributive expansion for reduced complexity, plain variable clauses
The clause sub-matrix S5 defines a set of reliable implicants, which is in turn the defining set for the prime implicants of this problem. In fact it is equivalent to the set of prime implicants in this case.
Amortized distributive expansion for reduced complexity, conjunctive literal clauses:

Distributive expansion for reduced complexity, conjunctive literal clauses
The clause sub-matrix S5 defines a set of reliable implicants, which is in turn the defining set for the implicants of this problem (no longer for the prime implicants!). Their advantage is, that they are unique, which facilitates counting solutions.
Solving Strategies
If desired, a traditional decision algorithm can be implemented on top of the satoku matrix. As well as a traditional selection algorithm. Graph algorithms can also be run, although I have no idea (yet) what they actually do.
But why restrict yourself to a single possibility, if you can have it all?
The natural goal for the satoku matrix is to reduce the problem to a set of 2-SAT problems. A 2-SAT satoku matrix is necessarily free of terminal contradictions or terminates as unsatisfiable, after a single run of the requirements update algorithm (hence the m-complexity of ⌈k ⁄ 2⌉m instead of km ).
If a selection row is present, which reduces the k-SAT problem to a 2-SAT problem, the selection can simply be made to verify it and generate a set of reliable assignments.
If the encoding variables are suitable, it is possible to find a set of variables R , where every conjunction of those variables (r0∧r1∧...∧ri), ri ∈ R reduces the k-SAT problem to a 2-SAT problem. This results in an effective n-complexity of 2|R| . This is the reason for the dependency from encoding variables observed for decision algorithms.
|:todo:| move somewhere else?
For 2-SAT problems the clause bias can be chosen in such a manner, that the number of clauses becomes minimal. This generates reliable assignments of maximal length.
It really depends on the actual state of the matrix which strategy is best.
Here is a good random 3-SAT example, showing clearly that sometimes a simple deduction from the state of specific selection rows is better than any decision at all. (I'm just kidding! I will construct a better example when there is time. Right now it shows, that some more clauses can also be handled.)
043-CHECK-07-genAlea-40-171-LONG.pmaxc.x.v-001.png
Anyway, after matrix construction, the matrix delivers the following information without any decisions whatsoever:
There is one unconditionally required core assignment, i.e. it is the common subset of all implicants. These variables are determined and cannot be assigned otherwise:
[ 1 1 0 _ 1 _ 0 _ _ _ _ _ _ _ _ _ _ _ _ _ 0 _ 0 _ _ 0 _ 0 _ _ _ _ 0 _ _ 1 _ _ 1 _ ]
There are 2 fully verifiable selections (they reduce the k-SAT problem to a 2-SAT/1-SAT problem). Their reliable assignments are:
[ 1 1 0 1 1 1 0 0 0 1 0 0 1 1 0 0 1 _ 1 0 0 1 0 0 1 0 1 0 1 1 0 1 0 1 1 1 1 1 1 1 ] [ 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 0 1 0 1 0 0 1 0 0 _ 0 1 0 1 1 _ 1 0 _ 1 1 1 1 1 0 ] [ 1 1 0 _ 1 1 0 0 0 _ 0 0 1 1 0 _ 1 1 _ 0 0 1 0 0 1 0 1 0 1 1 0 1 0 1 1 1 1 1 1 1 ]
2 of the reliable assignments are also implicants:
[ 1 1 0 1 1 1 0 0 0 1 0 0 1 1 0 0 1 _ 1 0 0 1 0 0 1 0 1 0 1 1 0 1 0 1 1 1 1 1 1 1 ] [ 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 0 1 0 1 0 0 1 0 0 _ 0 1 0 1 1 _ 1 0 _ 1 1 1 1 1 0 ]
1 reliable assignment is not an implicant:
[ 1 1 0 _ 1 1 0 0 0 _ 0 0 1 1 0 _ 1 1 _ 0 0 1 0 0 1 0 1 0 1 1 0 1 0 1 1 1 1 1 1 1 ] ----------------------------------------------------------------------------------- [ _ _ _ 0 _ _ _ _ _ _ _ _ _ _ _ 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ] [ _ _ _ 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ 1 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ] [ _ _ _ _ _ _ _ _ _ 1 _ _ _ _ _ 1 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ]
And this is what you get from a decision algorithm:
==================================[MINISAT]=================================== | Conflicts | ORIGINAL | LEARNT | Progress | | | Clauses Literals | Limit Clauses Literals Lit/Cl | | ============================================================================== | 0 | 171 513 | 57 0 0 nan | 0.000 % | ============================================================================== restarts : 1 conflicts : 29 (inf /sec) decisions : 45 (inf /sec) propagations : 397 (inf /sec) conflict literals : 106 (20.90 % deleted) Memory used : 1.66 MB CPU time : 0 s SATISFIABLE
So it takes 45 dangerously exponential decisions to find out, that the problem is satisfiable.
And the other one:
c This is CryptoMiniSat 2.9.8 c restarts : 1 c conflicts : 29 (inf / sec) c decisions : 41 (0.00 % random) c conflict literals : 116 (31.36 % deleted) s SATISFIABLE v 1 2 -3 -4 5 6 -7 -8 -9 10 -11 -12 13 14 -15 -16 17 -18 -19 -20 -21 22 -23 -24 25 -26 27 -28 29 30 -31 32 -33 34 35 36 37 38 39 40 0
The solution fits the required core assignment perfectly:
[ 1 1 0 _ 1 _ 0 _ _ _ _ _ _ _ _ _ _ _ _ _ 0 _ 0 _ _ 0 _ 0 _ _ _ _ 0 _ _ 1 _ _ 1 _ ] // core assignment [ 1 1 0 0 1 1 0 0 0 1 0 0 1 1 0 0 1 0 0 0 0 1 0 0 1 0 1 0 1 1 0 1 0 1 1 1 1 1 1 1 ] // solution
Structural Decomposition of Regular XORSAT
Case 1 of Experiment
Regular XORSAT, 3-SAT, original problem (case 1 of experiment):
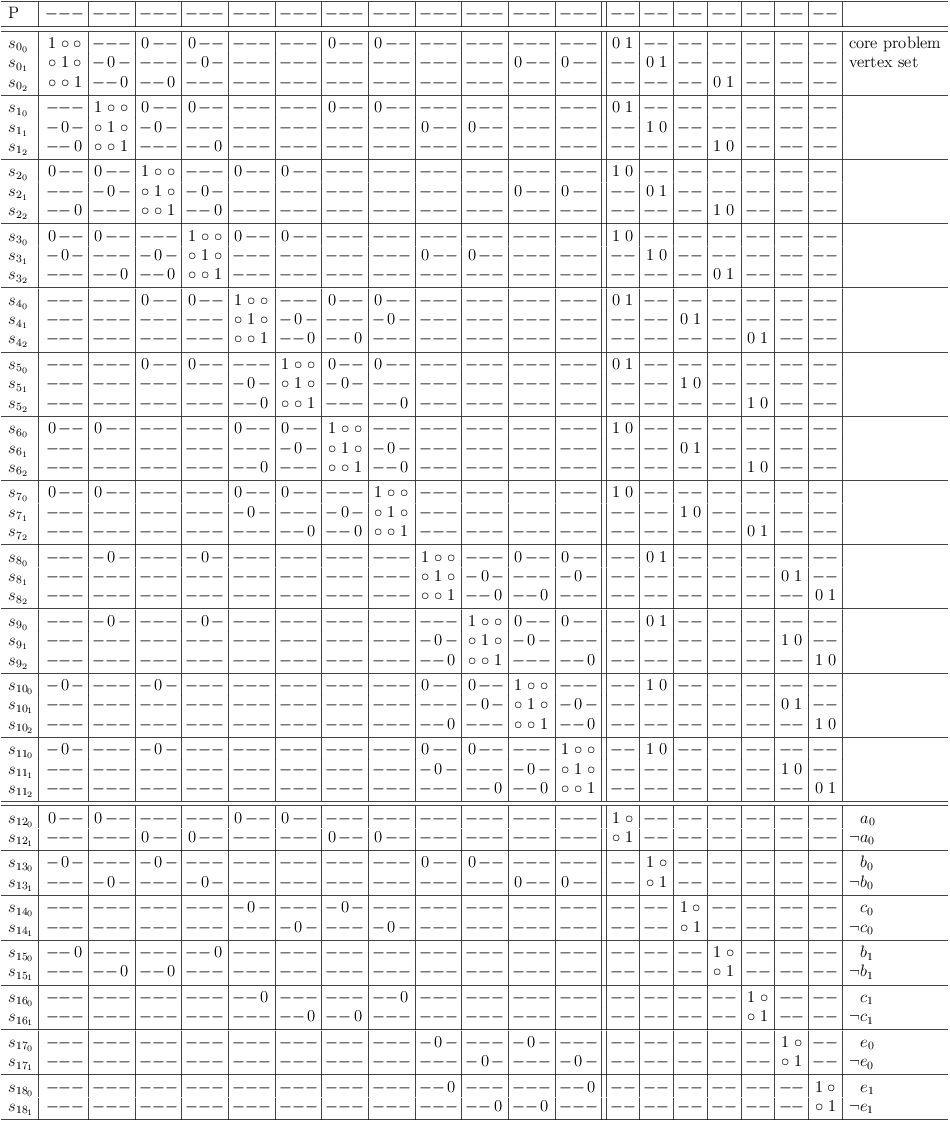
Regular XORSAT, 3-SAT, original problem
Case 2 of Experiment
Regular XORSAT, 3-SAT, satoku matrix stage 1, added conflicts (base problem for case 2 of experiment)
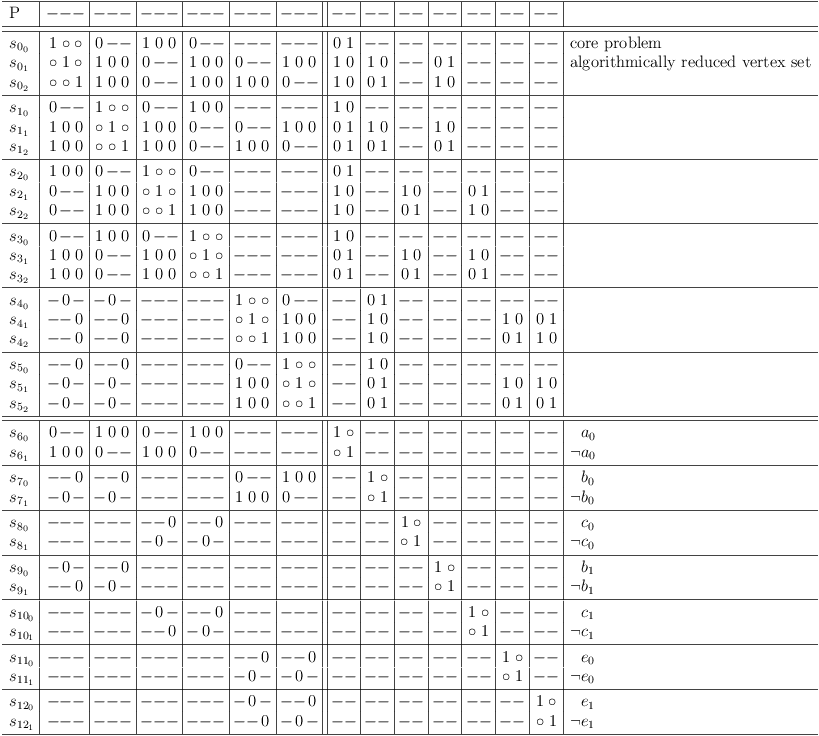
Regular XORSAT, 3-SAT, satoku matrix stage 1, added conflicts
Regular XORSAT, 3-SAT, satoku matrix stage 1, reencoded as independent set problem (case 2 of experiment):
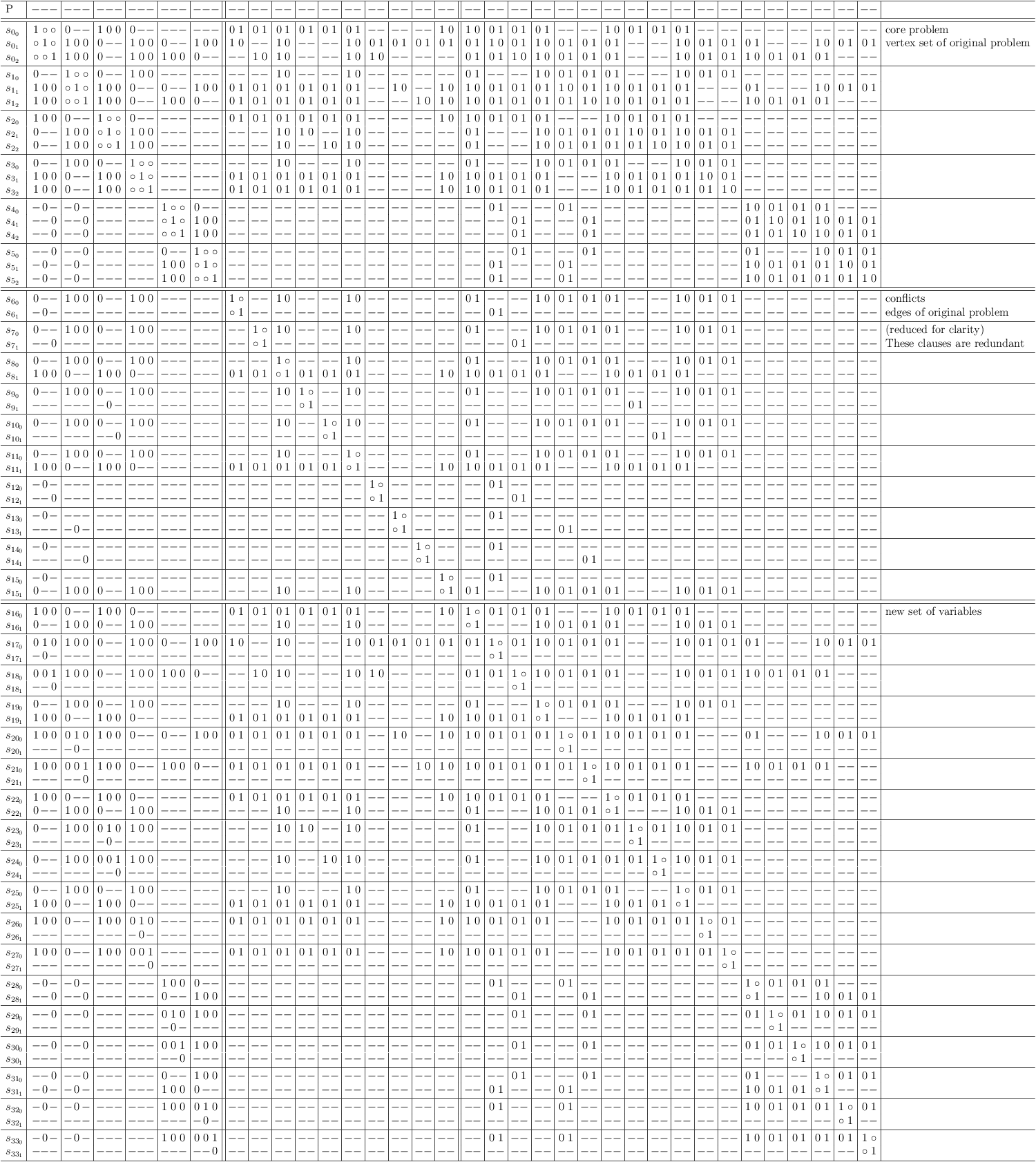
Regular XORSAT, 3-SAT, satoku matrix stage 1, reencoded as independent set problem
Regular XORSAT, 3-SAT, satoku matrix stage 1, reencoded as independent set problem, SAT solver perspective:
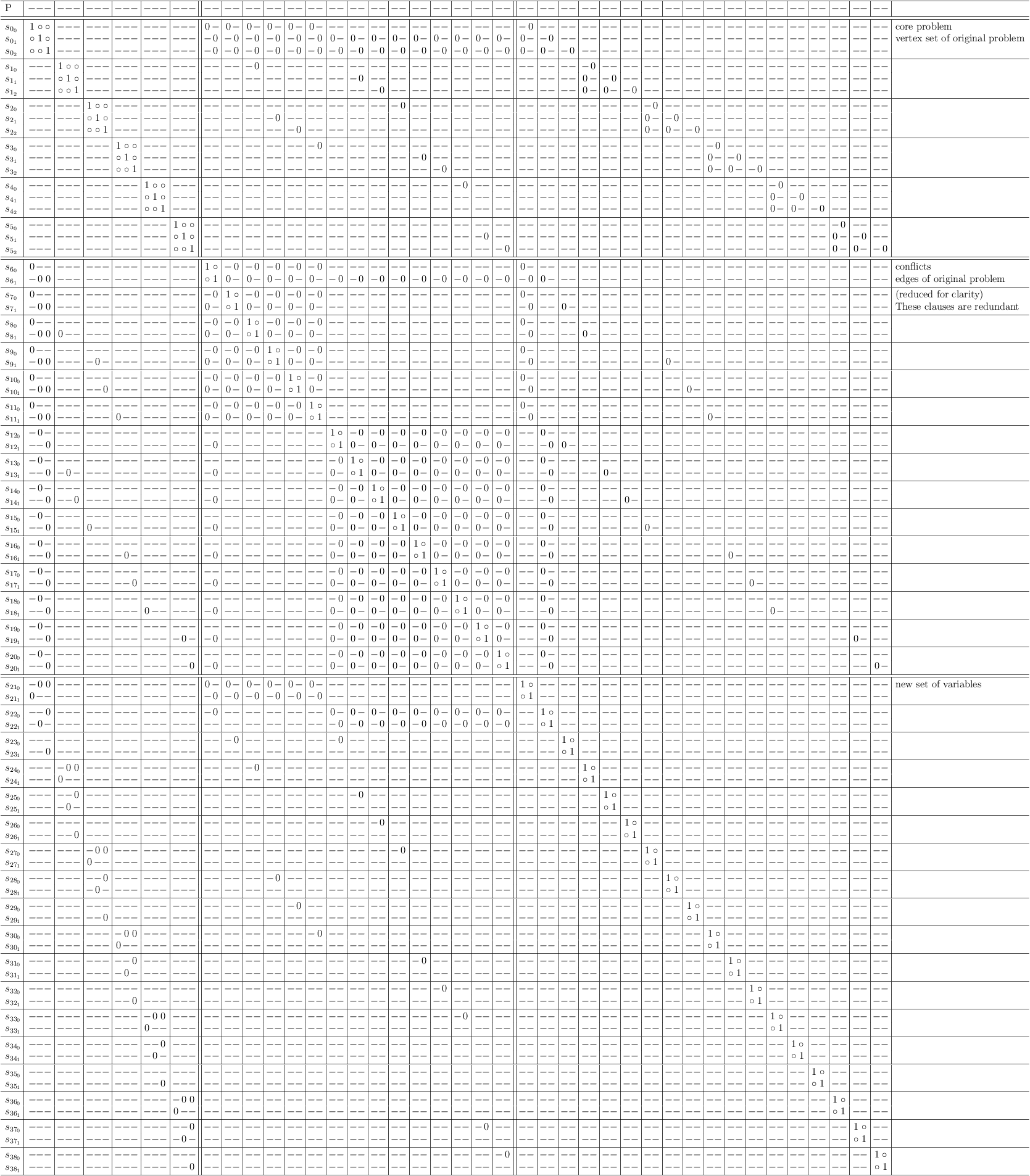
Regular XORSAT, 3-SAT, satoku matrix stage 1, reencoded as independent set problem, SAT solver perspective
Case 3 of Experiment
Regular XORSAT, 3-SAT, reencoded as selection problem (case 3 of experiment):
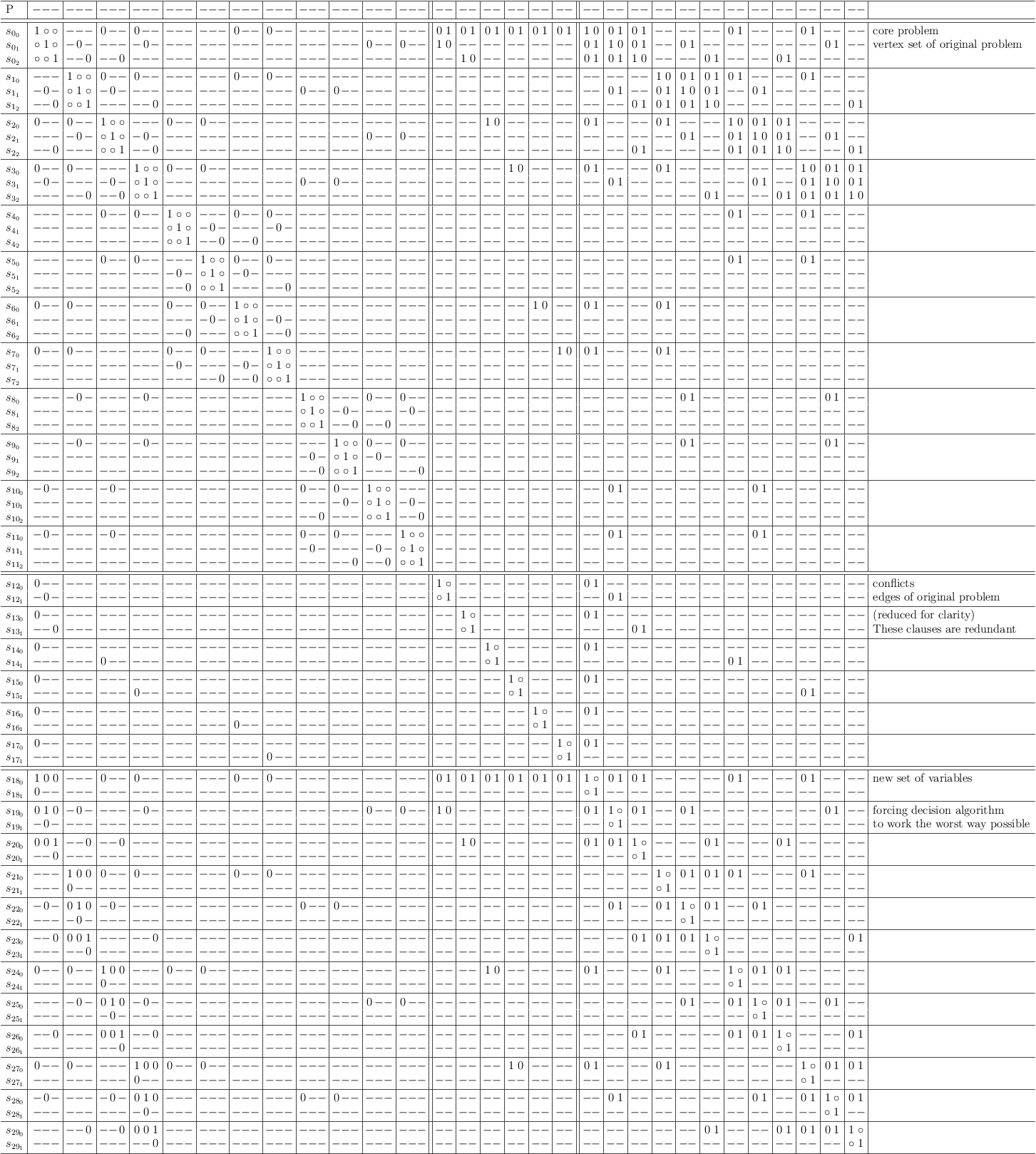
Regular XORSAT, 3-SAT, reencoded as selection problem
Full Logs of SAT-Solver Experiment
MiniSat_v1.14_linux
mod2-3cage-unsat-9-10.cnf:
$ MiniSat_v1.14_linux mod2-3cage-unsat-9-10.cnf ==================================[MINISAT]=================================== | Conflicts | ORIGINAL | LEARNT | Progress | | | Clauses Literals | Limit Clauses Literals Lit/Cl | | ============================================================================== | 0 | 232 696 | 77 0 0 nan | 0.000 % | | 100 | 232 696 | 84 100 1823 18.2 | 0.013 % | | 251 | 232 696 | 93 132 1925 14.6 | 0.013 % | | 477 | 232 696 | 102 91 1132 12.4 | 0.013 % | | 814 | 232 696 | 112 139 1844 13.3 | 0.013 % | | 1320 | 232 696 | 124 116 1428 12.3 | 0.013 % | | 2079 | 232 696 | 136 95 1165 12.3 | 0.013 % | | 3218 | 232 696 | 150 149 2035 13.7 | 0.013 % | | 4926 | 232 696 | 165 145 2098 14.5 | 0.013 % | | 7488 | 232 696 | 181 120 1561 13.0 | 0.013 % | | 11332 | 232 696 | 199 169 2534 15.0 | 0.013 % | | 17099 | 232 696 | 219 155 1878 12.1 | 0.013 % | | 25748 | 232 696 | 241 141 1708 12.1 | 0.013 % | | 38723 | 232 696 | 265 261 3340 12.8 | 0.013 % | | 58185 | 232 696 | 292 251 3162 12.6 | 0.013 % | | 87377 | 232 696 | 321 305 4116 13.5 | 0.013 % | | 131167 | 232 696 | 353 182 2295 12.6 | 0.013 % | | 196852 | 232 696 | 389 236 2756 11.7 | 0.013 % | | 295379 | 232 696 | 428 362 4849 13.4 | 0.013 % | | 443168 | 232 696 | 470 305 3873 12.7 | 0.013 % | | 664851 | 232 696 | 518 389 4560 11.7 | 0.013 % | | 997376 | 232 696 | 569 499 6237 12.5 | 0.013 % | | 1496165 | 232 696 | 626 314 3871 12.3 | 0.013 % | | 2244348 | 232 696 | 689 589 8167 13.9 | 0.014 % | | 3366623 | 233 696 | 758 665 8210 12.3 | 0.027 % | | 5050035 | 229 684 | 834 482 5464 11.3 | 1.163 % | ============================================================================== restarts : 26 conflicts : 6516168 (203110 /sec) decisions : 9885877 (308144 /sec) propagations : 92282116 (2876445 /sec) conflict literals : 87119249 (19.39 % deleted) Memory used : 2.05 MB CPU time : 32.082 s UNSATISFIABLE
mod2-3cage-unsat-9-10-vertex-cover-with-conflicts-red-elim.cnf:
$ MiniSat_v1.14_linux mod2-3cage-unsat-9-10-vertex-cover-with-conflicts-red-elim.cnf ==================================[MINISAT]=================================== | Conflicts | ORIGINAL | LEARNT | Progress | | | Clauses Literals | Limit Clauses Literals Lit/Cl | | ============================================================================== | 0 | 1730 3576 | 576 0 0 nan | 0.000 % | | 101 | 1730 3576 | 633 101 2881 28.5 | 0.001 % | | 252 | 1731 3576 | 696 251 6098 24.3 | 0.001 % | | 478 | 1734 3576 | 766 474 10979 23.2 | 0.001 % | | 816 | 1738 3576 | 843 808 19184 23.7 | 0.001 % | | 1324 | 1740 3576 | 927 777 20474 26.4 | 0.001 % | | 2083 | 1751 3576 | 1020 1038 25913 25.0 | 0.002 % | | 3223 | 1754 3576 | 1122 1026 22338 21.8 | 0.001 % | | 4931 | 1774 3576 | 1234 816 21661 26.5 | 0.001 % | | 7493 | 1784 3576 | 1358 1285 36315 28.3 | 0.001 % | | 11337 | 1791 3576 | 1493 1460 42005 28.8 | 0.001 % | | 17103 | 1800 3576 | 1643 1581 50885 32.2 | 0.001 % | | 25753 | 1807 3576 | 1807 1542 42402 27.5 | 0.001 % | | 38730 | 1830 3576 | 1988 1060 27313 25.8 | 0.001 % | | 58192 | 1842 3576 | 2187 1161 29061 25.0 | 0.001 % | | 87385 | 1861 3576 | 2406 1229 31548 25.7 | 0.001 % | | 131174 | 1879 3576 | 2646 1724 45714 26.5 | 0.001 % | | 196858 | 1887 3576 | 2911 2024 66899 33.1 | 0.001 % | | 295386 | 1895 3576 | 3202 1750 58822 33.6 | 0.001 % | | 443175 | 1916 3576 | 3522 3059 104660 34.2 | 0.001 % | | 664859 | 1933 3576 | 3875 2945 102476 34.8 | 0.001 % | | 997385 | 1945 3576 | 4262 2460 85460 34.7 | 0.001 % | | 1496176 | 1949 3576 | 4688 2275 80916 35.6 | 0.001 % | | 2244358 | 1953 3576 | 5157 2566 88599 34.5 | 0.001 % | | 3366632 | 1954 3576 | 5673 3564 120184 33.7 | 0.001 % | | 5050045 | 1954 3576 | 6240 3859 121915 31.6 | 0.001 % | | 7575162 | 1960 3576 | 6864 4065 152471 37.5 | 0.001 % | | 11362839 | 1960 3576 | 7551 6923 219702 31.7 | 0.007 % | | 17044352 | 1960 3576 | 8306 6207 177760 28.6 | 0.007 % | | 25566625 | 1960 3576 | 9137 5991 215173 35.9 | 0.001 % | | 38350028 | 1960 3576 | 10050 5453 187002 34.3 | 0.001 % | | 57525135 | 1960 3576 | 11055 9157 344012 37.6 | 0.001 % | | 86287793 | 1960 3576 | 12161 8826 301639 34.2 | 0.001 % | | 129431781 | 1960 3576 | 13377 11976 461638 38.5 | 0.007 % | | 194147763 | 1960 3576 | 14715 9009 339113 37.6 | 0.001 % | | 291221737 | 1960 3576 | 16187 13619 520440 38.2 | 0.001 % | | 436832698 | 1961 3576 | 17805 11715 422829 36.1 | 0.012 % | ============================================================================== restarts : 37 conflicts : 492799432 (21651 /sec) decisions : 523453042 (22998 /sec) propagations : 32650223888 (1434474 /sec) conflict literals : 19118584028 (15.50 % deleted) Memory used : 28.08 MB CPU time : 22761.1 s UNSATISFIABLE
mod2-3cage-unsat-9-10-vertex-cover-without-conflicts.cnf:
$ MiniSat_v1.14_linux mod2-3cage-unsat-9-10-vertex-cover-without-conflicts.cnf ==================================[MINISAT]=================================== | Conflicts | ORIGINAL | LEARNT | Progress | | | Clauses Literals | Limit Clauses Literals Lit/Cl | | ============================================================================== | 0 | 2320 4872 | 773 0 0 nan | 0.000 % | | 100 | 2320 4872 | 850 100 2696 27.0 | 0.000 % | | 250 | 2320 4872 | 935 250 7730 30.9 | 0.000 % | | 475 | 2320 4872 | 1028 475 15025 31.6 | 0.000 % | | 813 | 2320 4872 | 1131 813 26086 32.1 | 0.000 % | | 1322 | 2320 4872 | 1244 1322 40334 30.5 | 0.000 % | | 2081 | 2320 4872 | 1369 783 18378 23.5 | 0.000 % | | 3220 | 2320 4872 | 1506 1108 31069 28.0 | 0.000 % | | 4929 | 2320 4872 | 1656 1230 32439 26.4 | 0.000 % | | 7492 | 2320 4872 | 1822 1874 64202 34.3 | 0.000 % | | 11336 | 2320 4872 | 2004 1689 54535 32.3 | 0.000 % | | 17102 | 2320 4872 | 2205 2206 92348 41.9 | 0.000 % | | 25752 | 2320 4872 | 2426 1703 65328 38.4 | 0.000 % | | 38727 | 2320 4872 | 2668 1945 77118 39.6 | 0.000 % | | 58188 | 2320 4872 | 2935 1915 71077 37.1 | 0.000 % | | 87382 | 2320 4872 | 3229 2012 76019 37.8 | 0.000 % | | 131173 | 2320 4872 | 3551 2072 75605 36.5 | 0.000 % | | 196858 | 2320 4872 | 3907 2105 72181 34.3 | 0.000 % | | 295385 | 2320 4872 | 4297 3485 127768 36.7 | 0.000 % | | 443174 | 2320 4872 | 4727 3926 177139 45.1 | 0.000 % | | 664860 | 2320 4872 | 5200 4542 209943 46.2 | 0.000 % | | 997387 | 2320 4872 | 5720 3700 156595 42.3 | 0.000 % | | 1496175 | 2320 4872 | 6292 4308 191208 44.4 | 0.000 % | | 2244358 | 2320 4872 | 6921 3566 159429 44.7 | 0.000 % | | 3366633 | 2320 4872 | 7613 4742 234022 49.4 | 0.000 % | | 5050044 | 2320 4872 | 8375 7289 326987 44.9 | 0.000 % | | 7575163 | 2320 4872 | 9212 7408 339034 45.8 | 0.000 % | | 11362840 | 2320 4872 | 10134 5888 214951 36.5 | 0.000 % | | 17044352 | 2320 4872 | 11147 6992 321011 45.9 | 0.000 % | | 25566622 | 2320 4872 | 12262 7620 324590 42.6 | 0.000 % | | 38350025 | 2320 4872 | 13488 9132 447983 49.1 | 0.000 % | | 57525131 | 2320 4872 | 14837 8502 373241 43.9 | 0.000 % | | 86287791 | 2320 4872 | 16320 12710 621498 48.9 | 0.000 % | | 129431780 | 2320 4872 | 17953 14970 801196 53.5 | 0.000 % | | 194147763 | 2320 4872 | 19748 10371 514816 49.6 | 0.000 % | | 291221738 | 2320 4872 | 21723 13446 680208 50.6 | 0.000 % | | 436832698 | 2320 4872 | 23895 12423 624677 50.3 | 0.000 % | | 655249138 | 2320 4872 | 26285 13921 733198 52.7 | 0.000 % | | 982873799 | 2320 4872 | 28913 16449 748971 45.5 | 0.000 % | | 1474310791 | 2320 4872 | 31804 19079 886125 46.4 | 0.000 % | | -2083501017 | 2320 4872 | 34985 23194 1083272 46.7 | 0.000 % | | -977767784 | 2320 4872 | 38483 28154 1360430 48.3 | 0.000 % | | 680832066 | 2320 4872 | 42332 17063 858971 50.3 | 0.000 % | *** INTERRUPTED *** restarts : 43 conflicts : 10835521721 (13930 /sec) decisions : 12838157330 (16504 /sec) propagations : 1071321181196 (1377230 /sec) conflict literals : 571262903478 (15.21 % deleted) Memory used : 147.38 MB CPU time : 777881 s *** INTERRUPTED ***
cryptominisatLinux64
mod2-3cage-unsat-9-10.cnf:
$ cryptominisatLinux64 mod2-3cage-unsat-9-10.cnf c Outputting solution to console c This is CryptoMiniSat 2.9.8 c Finding non-binary XORs: 0.00 s (found: 32, avg size: 3.8) c conflicts : 158517 (185611.88 / sec) c decisions : 197651 (0.85 % random) c bogo-props : 393560907 (460831202.64 / sec) c conflict literals : 2699507 (17.83 % deleted) c Memory used : 37.68 MB c CPU time : 0.85 s s UNSATISFIABLE
Full log mod2-3cage-unsat-9-10.cnf.log.crypto.
mod2-3cage-unsat-9-10-vertex-cover-with-conflicts-red-elim.cnf:
$ cryptominisatLinux64 mod2-3cage-unsat-9-10-vertex-cover-with-conflicts-red-elim.cnf c This is CryptoMiniSat 2.9.8 *** INTERRUPTED *** c num threads : 1 c restarts : 415 c dynamic restarts : 118 c static restarts : 297 c full restarts : 7 c total simplify time : 0.01 c learnts DL2 : 0 c learnts size 2 : 1649 c learnts size 1 : 0 (0.00 % of vars) c filedLit time : 121.38 (0.16 % time) c v-elim SatELite : 116 (33.33 % vars) c SatELite time : 3924.53 (5.33 % time) c v-elim xor : 0 (0.00 % vars) c xor elim time : 6.58 (0.01 % time) c num binary xor trees : 3 c binxor trees' crown : 7 (2.33 leafs/tree) c bin xor find time : 0.00 c OTF clause improved : 753548 (0.01 clauses/conflict) c OTF impr. size diff : 865263 (1.15 lits/clause) c OTF cl watch-shrink : 75306345 (0.87 clauses/conflict) c OTF cl watch-sh-lit : 526543155 (6.99 lits/clause) c tried to recurMin cls : 4345605 (5.02 % of conflicts) c updated cache : 67090 (0.02 lits/tried recurMin) c clauses over max glue : 0 (0.00 % of all clauses) c conflicts : 86498724 (1175.00 / sec) c decisions : 90622941 (0.10 % random) c bogo-props : 16863905858054 (229078816.06 / sec) c conflict literals : 2926984465 (35.30 % deleted) c Memory used : 1307.41 MB c CPU time : 73616.17 s
Full log mod2-3cage-unsat-9-10-vertex-cover-with-conflicts-red-elim.cnf.log.crypto.
mod2-3cage-unsat-9-10-vertex-cover-without-conflicts.cnf:
$ cryptominisatLinux64 mod2-3cage-unsat-9-10-vertex-cover-without-conflicts.cnf c This is CryptoMiniSat 2.9.8 *** INTERRUPTED *** c num threads : 1 c restarts : 163482 c dynamic restarts : 163209 c static restarts : 273 c full restarts : 7 c total simplify time : 0.30 c learnts DL2 : 0 c learnts size 2 : 2088 c learnts size 1 : 0 (0.00 % of vars) c filedLit time : 129.57 (0.18 % time) c v-elim SatELite : 232 (33.33 % vars) c SatELite time : 27678.63 (37.69 % time) c v-elim xor : 0 (0.00 % vars) c xor elim time : 12.76 (0.02 % time) c num binary xor trees : 0 c binxor trees' crown : 0 (-nan leafs/tree) c bin xor find time : 0.00 c OTF clause improved : 1726122 (0.01 clauses/conflict) c OTF impr. size diff : 2161892 (1.25 lits/clause) c OTF cl watch-shrink : 107939754 (0.71 clauses/conflict) c OTF cl watch-sh-lit : 600143904 (5.56 lits/clause) c tried to recurMin cls : 6396250 (4.19 % of conflicts) c updated cache : 150519 (0.02 lits/tried recurMin) c clauses over max glue : 0 (0.00 % of all clauses) c conflicts : 152569643 (2077.75 / sec) c decisions : 211788006 (0.15 % random) c bogo-props : 12581748824367 (171343166.74 / sec) c conflict literals : 4818835838 (28.25 % deleted) c Memory used : 3297.49 MB c CPU time : 73430.12 s
Full log mod2-3cage-unsat-9-10-vertex-cover-without-conflicts.cnf.log.crypto.
lingeling
Full log mod2-3cage-unsat-9-10.cnf.log.ling.
Full log mod2-3cage-unsat-9-10-vertex-cover-with-conflicts.cnf.log.ling.
Full log mod2-3cage-unsat-9-10-vertex-cover-with-conflicts-red-elim.cnf.log.ling.
Full log mod2-3cage-unsat-9-10-vertex-cover-without-conflicts.cnf.log.ling.
treengeling
Full log mod2-3cage-unsat-9-10.cnf.log.tling.
Full log mod2-3cage-unsat-9-10-vertex-cover-with-conflicts.cnf.log.tling.
Full log mod2-3cage-unsat-9-10-vertex-cover-with-conflicts-red-elim.cnf.log.tling.
Full log mod2-3cage-unsat-9-10-vertex-cover-without-conflicts.cnf.log.tling.
| [1] | I will eventually document the satoku matrix in any case. However, if there is nothing new, I can spare myself the effort of annoying anybody else with my lack of mathematical knowledge. |
Copyright
Copyright (C) 2013, Wolfgang Scherer, <Wolfgang.Scherer@gmx.de>. See the document source for conditions of use under the GNU Free Documentation License.