Quickstart

Please, note:

• You are always looking at the same problem
• Every transformation is a simple propagation of requirements based on conflicting literals
• No complex analysis is done here
• No decision is ever made (except for demonstration)
• Complexity is  ≥ O(m²) (based on clauses, not variables), so it is not about ultimate speed at all times, however for a certain class of problems it is a lot faster than CDCL.

Overview

There are at least three ways to go about solving a propositional problem:

1. Map the clauses to a selection problem and apply algorithms from graph theory.

   Since it is also NP-complete, it does not seem interesting, especially, as it is unclear how the k-SAT clauses are recovered. However, 2-SAT problems are generally solved in polynomial time with graph algorithms.

2. Perform decisions over the set of variables.

   This does not solve 2-SAT problems in polynomial time, which seems counter-intuitive.

3. Perform distributive expansion over the clauses. The resulting DNF is known to produce all prime implicants for CNF problems.

   Since it is worst case exponential, it seems to be dismissed entirely.

   It is noteworthy, that partial distributive expansion is strictly polynomial and delivers partial assignments that must be part of a solution or they are a contradiciton. There is no "guessing" involved and it seems odd, that this technique is not used elsewhere.

The satoku matrix combines all three perspectives of SAT problems, however, no graph algorithms (which are too general) are applied in favor of partial distributive expansion. However, once the options of partial distributive expansion are exhausted, it is possible to continue with any variant of graph algorithms or decsion algorithms.

In the special case of a 2-SAT problem, the satoku matrix is either trivially satisfiable or shows unsatisfiability. No other algorithms are necessary. (This is now proved in Structural Logic).

Therefore, it is not necessary to reduce a k-SAT problem to a 1-SAT problem (as a variable based decision algorithm effectively does for the variable part). It is sufficient to reduce it to a (set of) (possibly mixed 1-SAT and) 2-SAT problems over the clauses of the selection problem. The complexity for a selection problem is therefore not k^m, but rather ⌈k ⁄ 2⌉^m, which for 3-SAT (and 4-SAT) is 2^m.

Note, that the complexity of 2-SAT is ⌈2 ⁄ 2⌉^m = 1^m, which is consistent with the fact, that it is trivially solvable, just as 1-SAT, ⌈1 ⁄ 2⌉^m = 1^m.

It can further be shown, that all 2-literal clauses of "direct encoding" problems can be be effectively ignored and even removed or replaced by more suitable ones, since they no longer contribute to the actual problem (which is to reduce the k-SAT region, k ≥ 3, to at least one 2+1-SAT instance).

This implies directly, that 3-SAT problems in "direct encoding" are harder for decisions over variables, since the number of 3-SAT clauses is less than or equal to the number of variables, and 2-SAT clauses cannot be ignored. In the worst case, a synthetic variable set that just enumerates all possible 2-literal partitions of the k-SAT clauses is far better than the provided variables.

The satoku matrix shows, that a decision algorithm over the variables is effectively a selection problem restricted to the variables, while a classic selection problem is restricted to the clauses. Separating them into graph theory (selection problem over the clauses) and decision problems (selection problems over the 2-literal variable clauses) does not achieve anything. The fact, that either is mathematically sufficient to solve a problem does not mean that having the full picture is worthless.

The satoku matrix further illustrates, that making decisions for variables does indeed reduce the k-SAT region to a mixed 2-SAT/1-SAT problem. The fact, that it can't be seen easily, if noone looks, does not mean that it is not the case.

It can be shown, that for regular XORSAT-problems, the complexity of the selection problem and the complexity of the decision problem become equivalent. The effect of making a decision for a variable then only affects two 4-literal clauses and no further implicit reductions of the selection problem region are triggered.

It can further be shown, that a simple re-encoding of such regular XORSAT problems (but also generally all CNF-problems) - in such a manner that only a single clause is affected by one alternative of a variable decision - makes solving the problem extremely much harder for decision algorithms ("direct encoding").

It can also be shown, that adding conflict maximization to a problem in direct encoding and subsequent re-encoding can make the problem easier for decision algorithms (very much easier in case of regular XORSAT).

The worst case for SAT problems are therefore problems, where variable decisions only have minimal effect and conflict maximization techniques cannot be applied. The Hirsch hgen8 problems are a good example.

XORSAT problems are generally not the worst case. Therefore, special XOR handling (of easily recognizable XORs) is not the final aspect of advanced SAT solving. The fact that XORs can trivially be made unrecognizable emphasizes the necessity of using suitable variable sets for decision algorithms.

Various consequences of the satoku matrix (namely the set of reliable assignments and conflict maximization without a suitable variable set) cannot be achieved in graph theory or propositional logic alone in polynomial time. Therefore, the fact that the satoku matrix is mathematically not necessary for solving logical problems does not mean it can simply be dismissed as not useful.

Example

Propositional formula:

( ¬a ∨ ¬b ∨ ¬f ) ∧
( ¬a ∨  b ∨  g ) ∧
( ¬a ∨  e ∨  g ) ∧
( ¬a ∨  d ∨  f ) ∧
( ¬a ∨  b ∨  d ) ∧
( ¬a ∨ ¬e ∨  f ) ∧
( ¬a ∨ ¬c ∨  g ) ∧
( ¬a ∨  f ∨  g ) ∧
(  a ∨  c ∨  e ) ∧
(  a ∨ ¬d ∨  g ) ∧
(  a ∨ ¬b ∨ ¬g ) ∧
(  a ∨ ¬d ∨ ¬f ) ∧
(  a ∨ ¬b ∨ ¬d ) ∧
(  a ∨ ¬c ∨  d ) ∧
(  a ∨ ¬b ∨ ¬c ) ∧
( ¬b ∨  c ∨  e ) ∧
( ¬b ∨  e ∨  f ) ∧
( ¬b ∨ ¬e ∨ ¬f ) ∧
( ¬b ∨ ¬c ∨  g ) ∧
(  b ∨  d ∨ ¬g ) ∧
(  b ∨  e ∨  g ) ∧
(  b ∨  d ∨  f ) ∧
(  b ∨ ¬d ∨  g ) ∧
( ¬c ∨ ¬e ∨  g ) ∧
(  c ∨  d ∨  f ) ∧
(  c ∨  f ∨ ¬g ) ∧
(  c ∨ ¬d ∨  f ) ∧
(  c ∨ ¬d ∨  e ) ∧
( ¬d ∨ ¬e ∨  g ) ∧
(  d ∨  e ∨ ¬g )

Clause vectors:

[ 0 0 _ _ _ 0 _ ]
[ 0 1 _ _ _ _ 1 ]
[ 0 _ _ _ 1 _ 1 ]
[ 0 _ _ 1 _ 1 _ ]
[ 0 1 _ 1 _ _ _ ]
[ 0 _ _ _ 0 1 _ ]
[ 0 _ 0 _ _ _ 1 ]
[ 0 _ _ _ _ 1 1 ]
[ 1 _ 1 _ 1 _ _ ]
[ 1 _ _ 0 _ _ 1 ]
[ 1 0 _ _ _ _ 0 ]
[ 1 _ _ 0 _ 0 _ ]
[ 1 0 _ 0 _ _ _ ]
[ 1 _ 0 1 _ _ _ ]
[ 1 0 0 _ _ _ _ ]
[ _ 0 1 _ 1 _ _ ]
[ _ 0 _ _ 1 1 _ ]
[ _ 0 _ _ 0 0 _ ]
[ _ 0 0 _ _ _ 1 ]
[ _ 1 _ 1 _ _ 0 ]
[ _ 1 _ _ 1 _ 1 ]
[ _ 1 _ 1 _ 1 _ ]
[ _ 1 _ 0 _ _ 1 ]
[ _ _ 0 _ 0 _ 1 ]
[ _ _ 1 1 _ 1 _ ]
[ _ _ 1 _ _ 1 0 ]
[ _ _ 1 0 _ 1 _ ]
[ _ _ 1 0 1 _ _ ]
[ _ _ _ 0 0 _ 1 ]
[ _ _ _ 1 1 _ 0 ]
  a b c d e f g

Dimacs and log files for Lingeling/CryptoMiniSat/MiniSat demonstrating different direct encoding variants:

030-genalea-30-7.cnf               // genAlea with seed 1733168555
030-genalea-30-7.pmaxc.c-000.mtx   // + conflicts                 => direct encoding
030-genalea-30-7.pmaxc.c-001.mtx   // + conflicts, - redundancies => direct encoding
030-genalea-30-7.pmaxc.r-000.mtx   // - conflicts                 => direct encoding

and the effect on the number of decisions:

030-genalea-30-7.cnf.log.ling:37:c 0 decisions, 0.0 decisions/sec
030-genalea-30-7.pmaxc.c-000.mtx+intra.cnf.log.ling:39:c 0 decisions, 0.0 decisions/sec
030-genalea-30-7.pmaxc.c-001.mtx+intra.cnf.log.ling:38:c 0 decisions, 0.0 decisions/sec
030-genalea-30-7.pmaxc.r-000.mtx+intra.cnf.log.ling:41:c 31 decisions, 11983.0 decisions/sec

030-genalea-30-7.cnf.log.crypto:100:c decisions                : 1           (100.00    % random)
030-genalea-30-7.pmaxc.c-000.mtx+intra.cnf.log.crypto:103:c decisions                : 3           (100.00    % random)
030-genalea-30-7.pmaxc.c-001.mtx+intra.cnf.log.crypto:101:c decisions                : 4           (50.00     % random)
030-genalea-30-7.pmaxc.r-000.mtx+intra.cnf.log.crypto:101:c decisions                : 15          (33.33     % random)

030-genalea-30-7.cnf.log.mini2.2.0:17:decisions             : 3              (0.00 % random) (inf /sec)
030-genalea-30-7.pmaxc.c-000.mtx+intra.cnf.log.mini2.2.0:18:decisions             : 4              (0.00 % random) (2545 /sec)
030-genalea-30-7.pmaxc.c-001.mtx+intra.cnf.log.mini2.2.0:18:decisions             : 6              (0.00 % random) (inf /sec)
030-genalea-30-7.pmaxc.r-000.mtx+intra.cnf.log.mini2.2.0:18:decisions             : 33             (0.00 % random) (inf /sec)

This is not a good example, since it is too small. See CDCL and Direct Encoding for a better test.

Simple Mapping

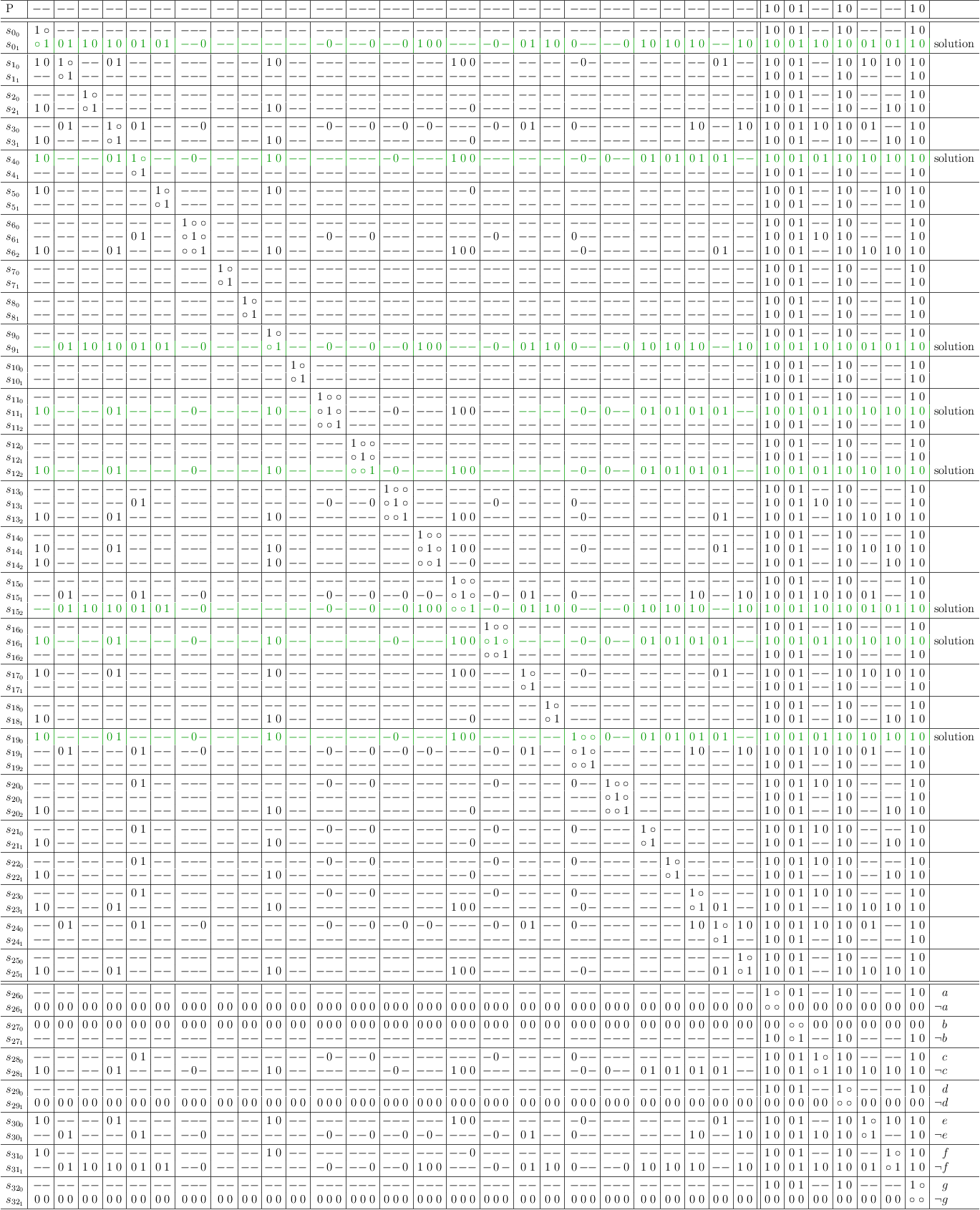
Satoku matrix, simple mapping without conflict maximization.

• the green region is the selection problem
• the blue region is the decision problem. Variables are mapped as 2-literal clauses, p↦(p∨¬p)
• the red region shows partial assignments for the variables

Decision Demonstration

Make a decision on variable a,  by disabling alternative ¬a. Observe, that this will actually reduce clauses S₀, .., S₇ to at least 2-literal clauses:

And solved! Observe, that not only clauses S₀, .., S₇ are reduced, but due to conflict propagation also some others to varying degrees. The solutions already appear in the partial assignments, although the variable region is not fully reduced to a 1-SAT instance yet:

A little clean up:

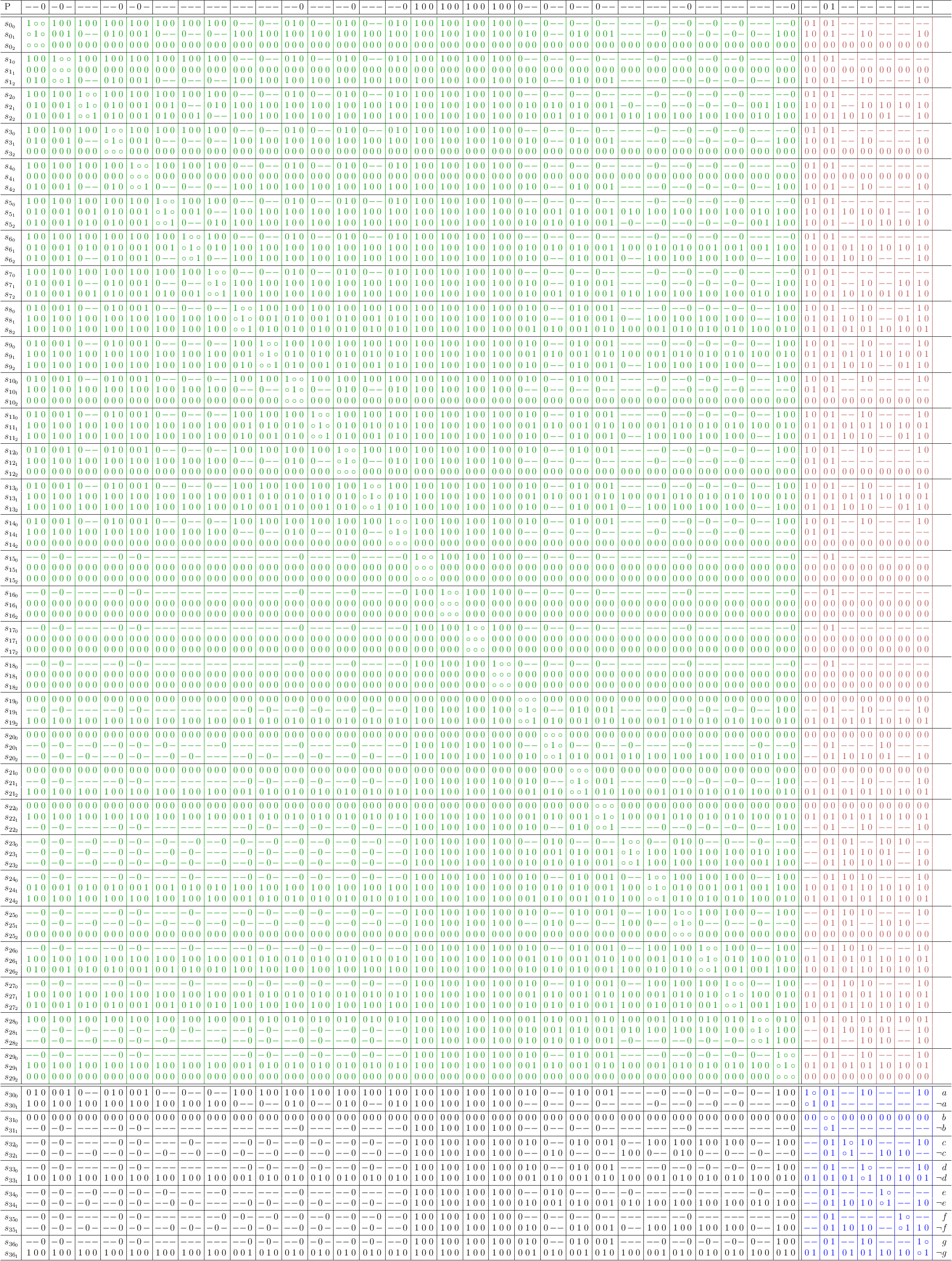
Conflict Maximization

Satoku matrix mapping with simple conflict maximization.

Logically equivalent conjunction of DNFs for the example propositional formula:

(( ¬a ) ∨ (  a ∧ ¬b ) ∨ (  a ∧  b ∧ ¬f )) ∧
(( ¬a ) ∨ (  a ∧  b ) ∨ (  a ∧ ¬b ∧  g )) ∧
(( ¬a ) ∨ (  a ∧  e ) ∨ (  a ∧ ¬e ∧  g )) ∧
(( ¬a ) ∨ (  a ∧  d ) ∨ (  a ∧ ¬d ∧  f )) ∧
(( ¬a ) ∨ (  a ∧  b ) ∨ (  a ∧ ¬b ∧  d )) ∧
(( ¬a ) ∨ (  a ∧ ¬e ) ∨ (  a ∧  e ∧  f )) ∧
(( ¬a ) ∨ (  a ∧ ¬c ) ∨ (  a ∧  c ∧  g )) ∧
(( ¬a ) ∨ (  a ∧  f ) ∨ (  a ∧ ¬f ∧  g )) ∧
((  a ) ∨ ( ¬a ∧  c ) ∨ ( ¬a ∧ ¬c ∧  e )) ∧
((  a ) ∨ ( ¬a ∧ ¬d ) ∨ ( ¬a ∧  d ∧  g )) ∧
((  a ) ∨ ( ¬a ∧ ¬b ) ∨ ( ¬a ∧  b ∧ ¬g )) ∧
((  a ) ∨ ( ¬a ∧ ¬d ) ∨ ( ¬a ∧  d ∧ ¬f )) ∧
((  a ) ∨ ( ¬a ∧ ¬b ) ∨ ( ¬a ∧  b ∧ ¬d )) ∧
((  a ) ∨ ( ¬a ∧ ¬c ) ∨ ( ¬a ∧  c ∧  d )) ∧
((  a ) ∨ ( ¬a ∧ ¬b ) ∨ ( ¬a ∧  b ∧ ¬c )) ∧
(( ¬b ) ∨ (  b ∧  c ) ∨ (  b ∧ ¬c ∧  e )) ∧
(( ¬b ) ∨ (  b ∧  e ) ∨ (  b ∧ ¬e ∧  f )) ∧
(( ¬b ) ∨ (  b ∧ ¬e ) ∨ (  b ∧  e ∧ ¬f )) ∧
(( ¬b ) ∨ (  b ∧ ¬c ) ∨ (  b ∧  c ∧  g )) ∧
((  b ) ∨ ( ¬b ∧  d ) ∨ ( ¬b ∧ ¬d ∧ ¬g )) ∧
((  b ) ∨ ( ¬b ∧  e ) ∨ ( ¬b ∧ ¬e ∧  g )) ∧
((  b ) ∨ ( ¬b ∧  d ) ∨ ( ¬b ∧ ¬d ∧  f )) ∧
((  b ) ∨ ( ¬b ∧ ¬d ) ∨ ( ¬b ∧  d ∧  g )) ∧
(( ¬c ) ∨ (  c ∧ ¬e ) ∨ (  c ∧  e ∧  g )) ∧
((  c ) ∨ ( ¬c ∧  d ) ∨ ( ¬c ∧ ¬d ∧  f )) ∧
((  c ) ∨ ( ¬c ∧  f ) ∨ ( ¬c ∧ ¬f ∧ ¬g )) ∧
((  c ) ∨ ( ¬c ∧ ¬d ) ∨ ( ¬c ∧  d ∧  f )) ∧
((  c ) ∨ ( ¬c ∧ ¬d ) ∨ ( ¬c ∧  d ∧  e )) ∧
(( ¬d ) ∨ (  d ∧ ¬e ) ∨ (  d ∧  e ∧  g )) ∧
((  d ) ∨ ( ¬d ∧  e ) ∨ ( ¬d ∧ ¬e ∧ ¬g ))

Mapping with conflict maximization, redundancies removed:

Rearrange for amortized distributive expansion:

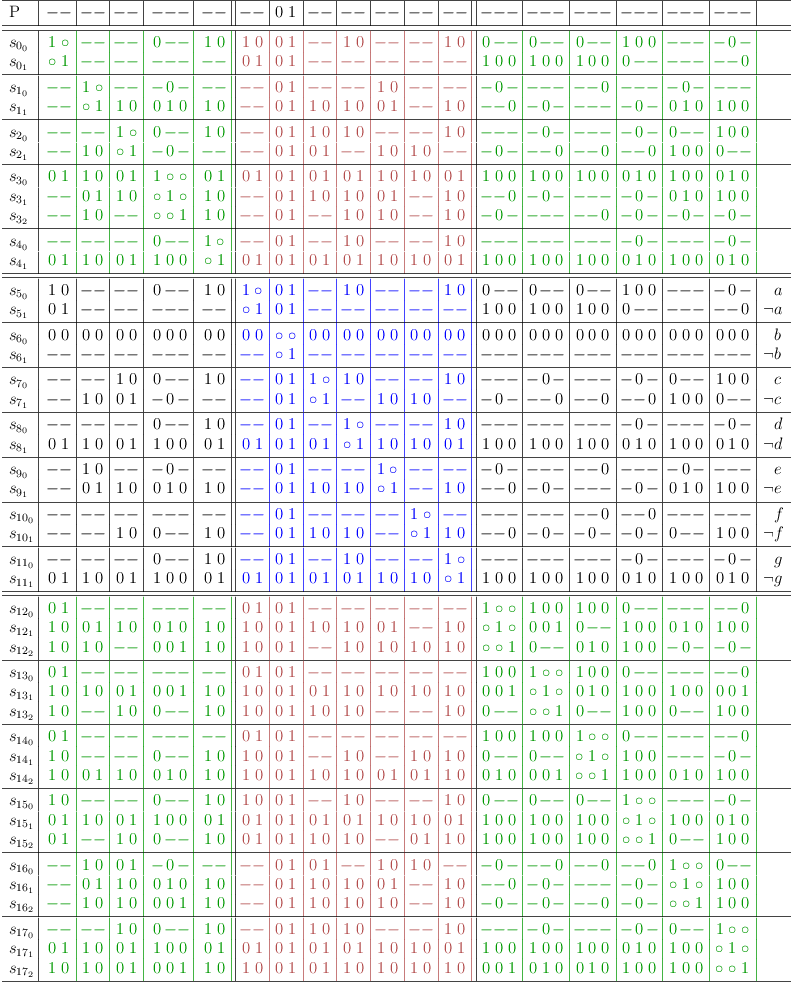
Distributive expansion: each pair of 3-literal clauses amounts to ⌈3 ⁄ 2⌉² = 4 necessary partitions. Their cartesian product, resulting in a 4-literal clause, only requires ⌈4 ⁄ 2⌉¹ = 2 partitions. This strictly reduces complexity and is sub-exponential, since only 4 instead of 9 combinations are required.

Further distributive expansion

Identify covered clauses, which can be removed as redundant:

Complete Set of All Possible Solutions

Remove covered clauses, complete set of solutions:

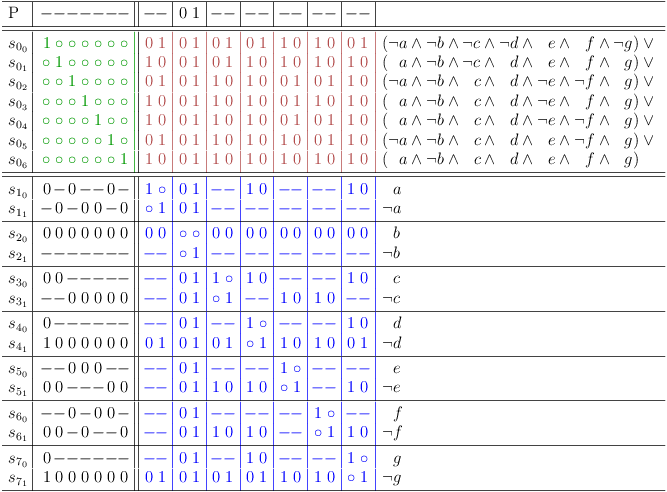
You can now start a decision algorithm over the variables, or you can just use one of the solutions.

Copyright

Copyright (C) 2013, Wolfgang Scherer, <Wolfgang.Scherer@gmx.de>. See the document source for conditions of use under the GNU Free Documentation License.