Scope

The experiments presented are not meant to be an all encompassing explanation of the consequences from re-encoding CNF problems. They provide only a small selection of effects to find a connection to current research in the field.

Should there be a technical reason, which invalidates the results, I am happy to provide measurements with any desired setup.

Environment

A set of 100 CNF problems was randomly generated by genAlea (3sat-toolbox-2003) with 40 variables and 171 clauses each. The problems are not trivially unsatisfiable.

The problem size was chosen large enough to show the effects significantly and small enough to acquire quick results.

The literals of the original problem clauses were sorted so that more frequent literals appear before less frequent literals. This provides the best conflict maximization.

A simple conflict maximization was applied to the CNF problem, based on the logical equivalence of:

(a ∨ b ∨ c ) = ((a) ∨ (¬a ∧ b) ∨ (¬a ∧ ¬b ∧ c))

Please, note, that this is just a simple shortcut for a technique, that can be generally applied to all propositional problems without the need of CNF encoding, or a "meaningful" set of variables for that matter. I.e., it can also be applied to problems which are only available in direct encoding.

Two versions of the problem with conflict maximization were produced. The first, "Cfl max.", is the problem with conflict maximization but without further operations applied and re-encoded with direct encoding. The second, "Cfl red.", is the problem with conflict maximization and additional removal of redundant clauses before re-encoding with direct encoding.

Finally, the problem was simply re-encoded as selection problem (independent set problem) in direct encoding, "Direct enc.", without any conflict maximization at all.

See section Visualization of Conflict Situation for further details. For a description of the logic applied, see Structural Logic.

The SAT solver Lingeling, Version ats 57807c8f410a9e676816984a0ad0c410e485bcae was used without any options to solve each variant of a problem. The number of decisions reported is an average over 5 runs of the solver for each variant.

Results

The common parameters for all solvers are the number of variables and clauses for the experiment.

The number of variables is necessarily constant for CNF (40) "Direct enc." (513),  and "Cfl max." (513). Since redundancy removal results vary, the number of variables necessarily varies for "Cfl red.", the average number of variables is 86.

The number of clauses is constant for CNF (171). The number of clauses for the versions in direct encoding depends on the number of conflicting literals between clauses. Therefore it is necessarily higher than for CNF. The average number of clauses for "Cfl max." is 97905,  for "Cfl red." 2934,  and for "Direct enc." 2309.

The number of clauses for direct encoding might appear to be constant due to scaling, however it is not. The relatively low variation is caused by the random generation of the experiments, which adds conflicting literals in a narrow range.

Conclusions

The increase in decsions from CNF to "Direct enc." is expected, because the number of variables and clauses increases significantly. Since the number of conflicts over the set of 3-literal clauses is actually the same, a closer relation in the number of necessary decisions could be expected. That this is not the case can be explained away with randomness of arbitrary decisions.

The decrease in decisions for "Cfl max." and "Cfl red." compared to CNF cannot be explained with a decrease in clauses, as "Cfl max." has strictly (and significantly) more clauses than CNF and "Cfl red.". There is also no decrease in the number of variables. Although "Cfl max." and "Cfl red." do not have strictly more variables, the number of variables is still significantly more on average.

The only real difference available for explanation is therefore, that the number of conflicts has also been increased significantly.

It can be generalized, that a problem in direct encoding with conflict maximization, "Cfl max., Cfl red.", is easier to solve than a problem in direct encoding without conflict maximization, "Direct enc." , iff the conflicts can actually be increased.

It cannot be be generalized, that a problem in direct encoding with conflict maximization, "Cfl max., Cfl red.", is easier to solve than a problem in CNF encoding. While this is the case for small unstructured problems, it is no longer the case for large and/or highly structured problems.

For the chosen problem size, conflict maximization alone already solves the problem trivially in most cases. I.e. in the satoku matrix, there would be no decision necessary at all (see Structural Logic).

This changes, when the problem size increases or the structure becomes more complex. Then exponentiality comes back into play and CNF may provide more structural insight (e.g. XORSAT).

However, for XORSAT, the structural information can be instantly diffused by direct encoding, so that current SAT solver are no longer able to detect it.

The effects can be explained quite easily and illustrative in the context of the satoku matrix. Other explanations may also be possible. However, there is a set of techniques to analyze and recover structural information that is not availabe outside the satoku matrix, i.e., in plain graph theory or propositional logic alone.

Visualization of Conflict Situation

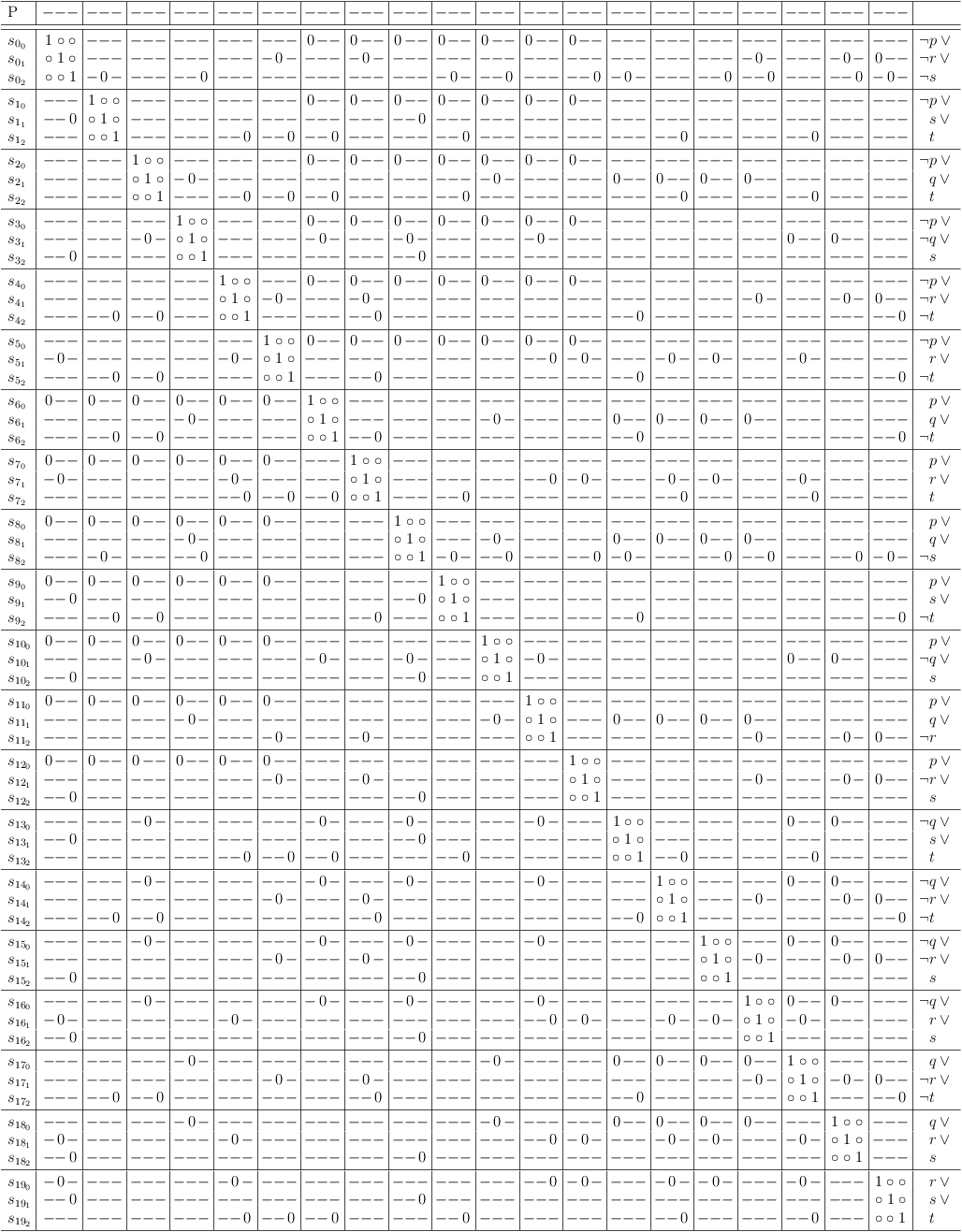
For a description of the satoku matrix, see Structural Logic.

For the purpose of conflict visualization, it is not necessary to understand, how the satoku matrix works. It can simply be viewed as inverted adjacency matrix, where the non-zero entries are classified by decision weakness. A strong connection between two partial solutions is denoted by 1,  while a weak connection is denoted as dash,  − .

The following propositional problem P is used as CNF:

( ¬p ∨ ¬r ∨ ¬s ) ∧
( ¬p ∨  s ∨  t ) ∧
( ¬p ∨  q ∨  t ) ∧
( ¬p ∨ ¬q ∨  s ) ∧
( ¬p ∨ ¬r ∨ ¬t ) ∧
( ¬p ∨  r ∨ ¬t ) ∧
(  p ∨  q ∨ ¬t ) ∧
(  p ∨  r ∨  t ) ∧
(  p ∨  q ∨ ¬s ) ∧
(  p ∨  s ∨ ¬t ) ∧
(  p ∨ ¬q ∨  s ) ∧
(  p ∨  q ∨ ¬r ) ∧
(  p ∨ ¬r ∨  s ) ∧
( ¬q ∨  s ∨  t ) ∧
( ¬q ∨ ¬r ∨ ¬t ) ∧
( ¬q ∨ ¬r ∨  s ) ∧
( ¬q ∨  r ∨  s ) ∧
(  q ∨ ¬r ∨ ¬t ) ∧
(  q ∨  r ∨  s ) ∧
(  r ∨  s ∨  t )

Direct mapping of P without conflict maximization renders the following satoku matrix, which is used to produce the "Direct enc." version:

Conflict maximization of P expands to the logically equivalent PM:

(( ¬p ) ∨ (  p ∧ ¬r ) ∨ (  p ∧  r ∧ ¬s )) ∧
(( ¬p ) ∨ (  p ∧  s ) ∨ (  p ∧ ¬s ∧  t )) ∧
(( ¬p ) ∨ (  p ∧  q ) ∨ (  p ∧ ¬q ∧  t )) ∧
(( ¬p ) ∨ (  p ∧ ¬q ) ∨ (  p ∧  q ∧  s )) ∧
(( ¬p ) ∨ (  p ∧ ¬r ) ∨ (  p ∧  r ∧ ¬t )) ∧
(( ¬p ) ∨ (  p ∧  r ) ∨ (  p ∧ ¬r ∧ ¬t )) ∧
((  p ) ∨ ( ¬p ∧  q ) ∨ ( ¬p ∧ ¬q ∧ ¬t )) ∧
((  p ) ∨ ( ¬p ∧  r ) ∨ ( ¬p ∧ ¬r ∧  t )) ∧
((  p ) ∨ ( ¬p ∧  q ) ∨ ( ¬p ∧ ¬q ∧ ¬s )) ∧
((  p ) ∨ ( ¬p ∧  s ) ∨ ( ¬p ∧ ¬s ∧ ¬t )) ∧
((  p ) ∨ ( ¬p ∧ ¬q ) ∨ ( ¬p ∧  q ∧  s )) ∧
((  p ) ∨ ( ¬p ∧  q ) ∨ ( ¬p ∧ ¬q ∧ ¬r )) ∧
((  p ) ∨ ( ¬p ∧ ¬r ) ∨ ( ¬p ∧  r ∧  s )) ∧
(( ¬q ) ∨ (  q ∧  s ) ∨ (  q ∧ ¬s ∧  t )) ∧
(( ¬q ) ∨ (  q ∧ ¬r ) ∨ (  q ∧  r ∧ ¬t )) ∧
(( ¬q ) ∨ (  q ∧ ¬r ) ∨ (  q ∧  r ∧  s )) ∧
(( ¬q ) ∨ (  q ∧  r ) ∨ (  q ∧ ¬r ∧  s )) ∧
((  q ) ∨ ( ¬q ∧ ¬r ) ∨ ( ¬q ∧  r ∧ ¬t )) ∧
((  q ) ∨ ( ¬q ∧  r ) ∨ ( ¬q ∧ ¬r ∧  s )) ∧
((  r ) ∨ ( ¬r ∧  s ) ∨ ( ¬r ∧ ¬s ∧  t ))

Note, that no new variables are introduced and that the set of possible solutions is therefore not only equivalent over a subset of variables, but it is identical over the entire set of variables.

Mapping of PM produces the following satoku matrix, which is directly encoded as "Cfl max.":

Removal of redundancies produces the following satoku matrix, which is directly encoded as "Cfl red.":

Copyright

Copyright (C) 2013, Wolfgang Scherer, <Wolfgang.Scherer@gmx.de>. See the document source for conditions of use under the GNU Free Documentation License.