Mapping a Logical Problem to a Satoku Matrix

Author: Wolfgang Scherer

Contents

Logical Problem

The logical problem:

(  p ∨  q ) ∧
( ¬p ∨  r )

is mapped step by step to a satoku matrix SM.

This is the clause vector representation of the base problem:

[ 1 1 _ ]
[ 0 _ 1 ]
  p q r

Satoku Matrix Requirements

The satoku matrix for mapping the logical problem needs 2 clause sub-matrixes S0, S1 with 2 possible selections each.

Mapping the variables to clause sub-matrixes with 2 posssible selections is not necessary, but it facilitates construction of the satoku matrix and better visualizes the problem structure.

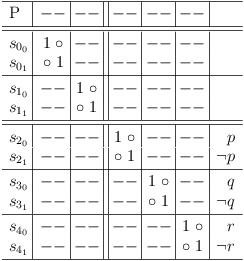
000-p-q-r.step.v-000.png

Satoku matrix for representation of (p∨q)∧(¬p∨r)

The logical interpretation of this SM is:

(s00∨s01)∧(s10∨s11)∧
(p∨¬p)∧(q∨¬q)∧(r∨¬r)

where s00, s01, s10, s11 stand for not yet specified literals. Adding the tautologies representing the necessary selection of either a variable or its negation does not change the set of possible solutions.

Map Clause (p∨q) Into Clause Sub-Matrix S0

The clause (p∨q) is mapped to clause sub-matrix S0 to illustrate the requirements update algorithm RUA.

Map literal p

Mapping a literal is performed by issuing a request for it. This is achieved by making the selection of the negated literal impossible, which in turn makes the selection of the literal a requirement.

Requesting literal p in clause sub-matrix S0 is performed by making the selection of literal ¬p impossible in clause segment cs00, 2 :

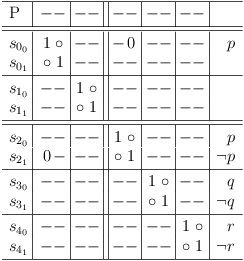
000-p-q-r.step.v-001.png

Requirements update for literal p in clause S0 is unspectacular, since there are no conflicts yet:

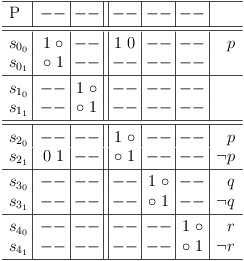
000-p-q-r.step.v-002.png

Map literal q

Mapping literal q into clause sub-matrix S0 is more interesting, since it detects consequences beyond the simple selection of the literal.

Request literal q in clause sub-matrix S0 :

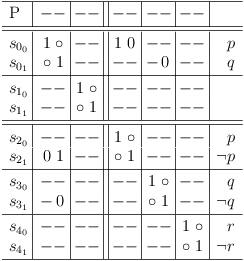
000-p-q-r.step.v-003.png

Requirements update for literal q in clause sub-matrix S0 : clause segment cs01, 3 :

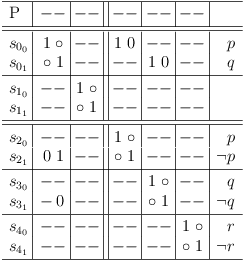
000-p-q-r.step.v-004.png

Requirements update for literal q in clause sub-matrix S0 : clause segment cs31, 0 :

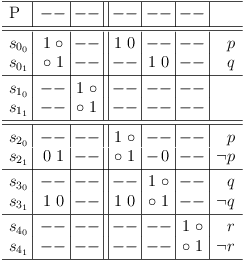
000-p-q-r.step.v-005.png

Requirements update for literal q in clause sub-matrix S0 : clause segment cs21, 3 :

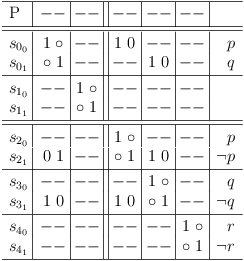
000-p-q-r.step.v-006.png

Interpretation of Consequences

The variable representations S2, S3 now show the consequences from the dependencies of clause sub-matrix S0 .

  • s21 represents the assignment of truth value F to variable p . The requirements specifiy, that in this case the truth value T must be assigned to variable q .
  • s31 represents the assignment of truth value F to variable q . The requirements specifiy, that in this case the truth value T must be assigned to variable p .

Map Clause (¬p∨r) Into Clause Sub-Matrix S1

The mapping of the logical problem is completed by mapping the clause (¬p∨r) into clause sub-matrix S1 .

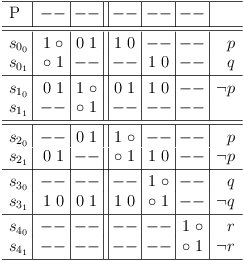
Request literal ¬p in clause sub-matrix S1 :

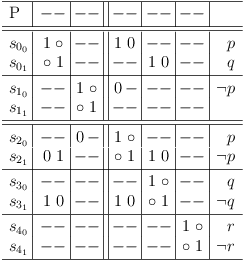
000-p-q-r.step.v-007.png

Requirements update for literal ¬p in clause sub-matrix S1 :

000-p-q-r.step.v-008.png

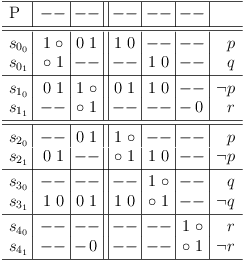
Request literal r in clause sub-matrix S1 :

000-p-q-r.step.v-009.png

Requirements update for literal r in clause sub-matrix S1 :

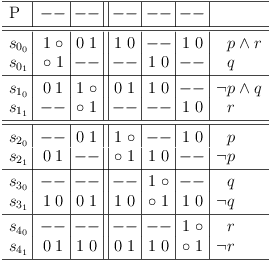
000-p-q-r.step.v-010.png

Distributive Expansion

Distributive expansion of a logical problem in conjunctive normal form CNF results in a disjunctive normal form DNF, where each clause represents a partial assignment of variables that solves the problem. All partial assignments are minimal. (Reference: Bronstein).

Distributive Expansion in a Satoku Matrix

Distributive expansion can be performed in a satoku matrix by combining several clause sub-matrixes into a single clause sub-matrix.

Add clause sub-matrix for all possible conjunctive combinations of clause sub-matrixes S0, S1 :

000-p-q-r.step.v-011.png

Add duplicate requests for selection rows s00, s01 :

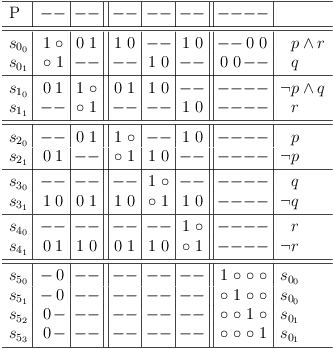
000-p-q-r.step.v-012.png

Add duplicate requests for selection rows s10, s11 :

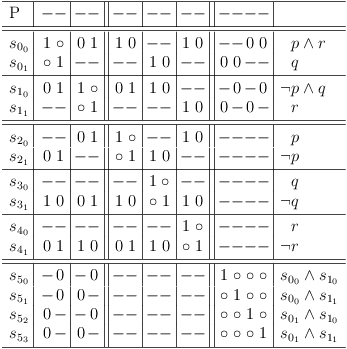
000-p-q-r.step.v-013.png

Requirements update:

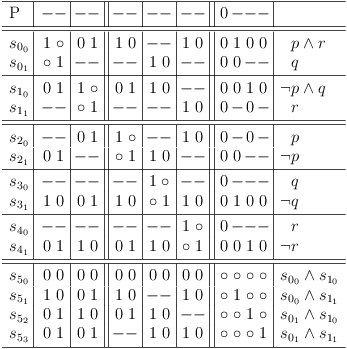
000-p-q-r.step.v-014.png

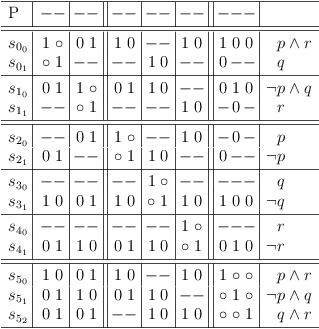
Minimal Conjunctive Assignments

Identify minimal conjunctions:

000-p-q-r.step.v-015.png

Copyright

Copyright (C) 2013, Wolfgang Scherer, <Wolfgang.Scherer@gmx.de>. See the document source for conditions of use under the GNU Free Documentation License.