2-SAT Solutions

Author:	Wolfgang Scherer

Contents

Base Problem
Distributive Expansion
- Set of Minimal Solutions
- Set of Unique Solutions
Micromal Solutions
- Direct Solution Retrieval
Verification of Partial Assignments

Old News

Distributive expansion of CNF problems resulting in a set of minimal partial solutions is well known.

News

Distributive expansion to retrieve a unique set of partial solutions.
Direct collection of partial solutions which are guaranteed to be satisfiable by successive clause elimination.

Base Problem

It is sufficient to use a very simple example to demonstrate the features of the different solution sets, that can be obtained with a satoku matrix.

Boolean formula:

(  p ∨  q ) ∧
( ¬p ∨  r ) ∧
(  q ∨ ¬s )

Clause vectors:

[ 1 1 _ _ ]
[ 0 _ 1 _ ]
[ _ 1 _ 0 ]
  p q r s

Distributive Expansion

Applying distributive expansion to a CNF boolean formula delivers a DNF formula, where each elementary conjunction represents a possibly partial solution for the CNF problem. These solutions are minimal, i.e., after assigning the truth values to the variables, each clause of the CNF problem has at least one literal which is true. Any remaining unassigned variables can be bound arbitrarily either way without changing the final result. (Found in an old issue of Bronstein).

As far as I am concerned, that is suffcient to define a solution. I really do not understand, that a proper solution should have to assign all variables. Especially with optimization in mind, minimal solutions are really the better way to go.

Here is the distributive expansion for the given example problem, done manually in the boolean way:

(  p ∨  q ) ∧ ( ¬p ∨  r ) ∧ (  q ∨ ¬s )

=> (  p  ∧ ( ¬p ∨  r ) ∧ (  q ∨ ¬s )) ∨
   (  q  ∧ ( ¬p ∨  r ) ∧ (  q ∨ ¬s ))

=> (((  p  ∧  ¬p ) ∨ (  p ∧  r )) ∧ (  q ∨ ¬s )) ∨
   (((  q  ∧  ¬p ) ∨ (  q ∧  r )) ∧ (  q ∨ ¬s ))

=> (  p ∧  r ∧ (  q ∨ ¬s )) ∨
   (  q ∧ ¬p ∧ (  q ∨ ¬s )) ∨
   (  q ∧  r ∧ (  q ∨ ¬s ))

=> (  p ∧  r ∧  q ) ∨
   (  p ∧  r ∧ ¬s ) ∨
   (  q ∧ ¬p ∧  q ) ∨
   (  q ∧ ¬p ∧ ¬s ) ∨
   (  q ∧  r ∧  q ) ∨
   (  q ∧  r ∧ ¬s )

=> (  p ∧  r ∧  q ) ∨
   (  p ∧  r ∧ ¬s ) ∨
   (  q ∧ ¬p ) ∨
   (  q ∧ ¬p ∧ ¬s ) ∨
   (  q ∧  r ) ∨
   (  q ∧  r ∧ ¬s )

=> (  p ∧  r ∧ ¬s ) ∨
   (  q ∧ ¬p ) ∨
   (  q ∧  r ) ∨

The result of the programmatic distributive expansion via clause vectors (satoku.py --expand):

[ 1 _ 1 0 ]
[ 0 1 _ _ ]
[ _ 1 1 _ ]
  p q r s

Set of Minimal Solutions

Basic mapping to a satoku matrix

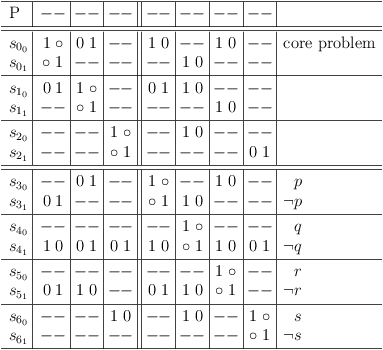
Basic mapping to a satoku matrix

Distributive expansion of core problem: Add quadruplicate requests for s_0₀, s_0₁, s_1₀, s_1₁, s_2₀, s_2₁

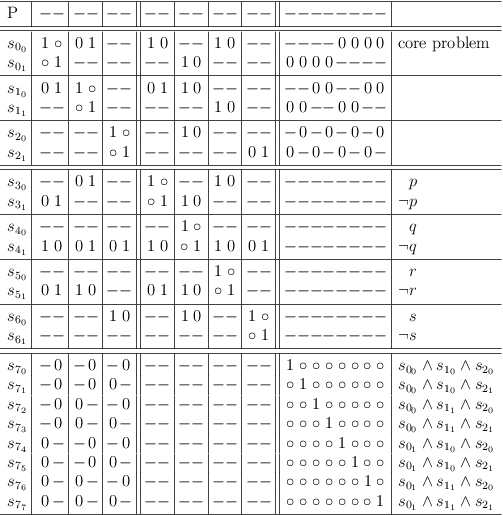
Distributive expansion of core problem: Add quadruplicate requests for s_0₀, s_0₁, s_1₀, s_1₁, s_2₀, s_2₁

Distributive expansion of core problem: Run RUA

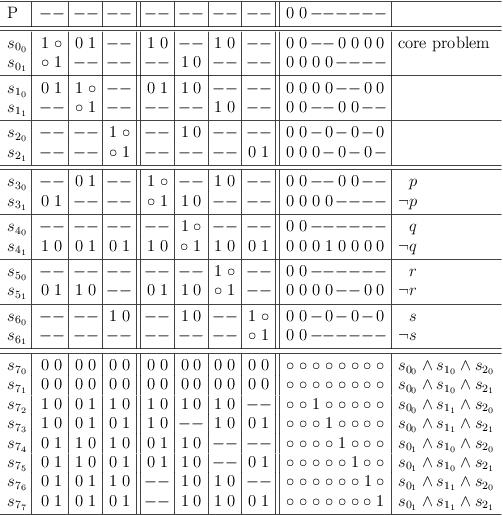
Distributive expansion of core problem: Run RUA

Distributive expansion of core problem: Remove contradictions, identify conjunctions

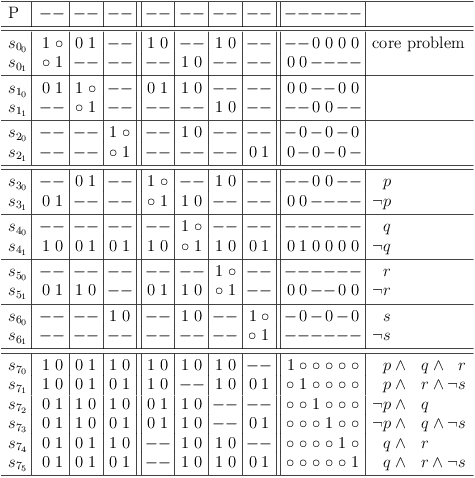
Distributive expansion of core problem: Remove contradictions, identify conjunctions

Remove redundant selections from solution set to obtain minimal solutions

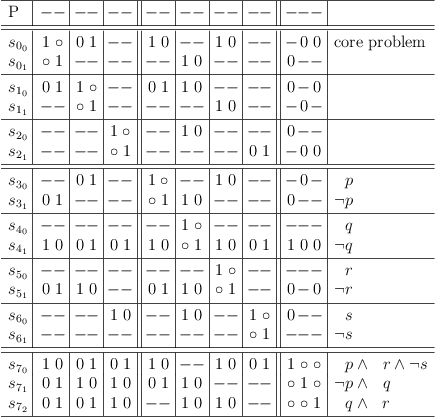
Remove redundant selections from solution set to obtain minimal solutions

=> (  p ∧  r ∧ ¬s ) ∨
   (  q ∧ ¬p ) ∨
   (  q ∧  r ) ∨

Set of Unique Solutions

Mapping to satoku matrix with conflict maximization

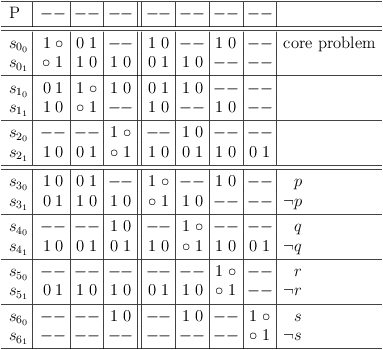
Mapping to satoku matrix with conflict maximization

Remove redundant clause in core problem, distributive expansion, identify unique solutions

Remove redundant clause in core problem, distributive expansion, identify unique solutions

Micromal Solutions

A micromal solution is a variable assignment that guarantees, that no matter which other assignments are made to satisfy as yet unsatisfied clauses consecutively, the result will still be a solution for the problem.

Note

See properly formalized version below (Verification of Partial Assignments).

This type of solution can be retrieved directly from the plain satoku matrix after requirements update. Choose any partial assignment in the intersecting region of the core problem and the variable region and convert it to a conjunctive clause vector ( s_2₁ ):

[ _ _ _ 0 ] // conjunction

Remove satisfied clauses from the original problem clause vectors:

[ _ _ _ 0 ] // solution (conjunction)
-----------
[ 1 1 _ _ ] // unsatisfied clauses (disjunctions)
[ 0 _ 1 _ ]
[ _ 1 _ 0 ]

=>

[ 1 1 _ _ ] // unsatisfied clauses
[ 0 _ 1 _ ]

Consecutively choose a literal from unsatisfied clauses, add it to the partial solution and remove the satisfied clauses:

[ 1 _ _ 0 ]
-----------
[ 1 1 _ _ ]
[ 0 _ 1 _ ]

=>

[ 0 _ 1 _ ]

Remove the negated literal from the unsatisfied clauses:

[ 1 _ _ 0 ]
-----------
[ 0 _ 1 _ ]

=>

[ _ _ 1 _ ]

Note, that if a single literal remains in a clause, it must be added to the partial solution immediately:

[ 1 _ 1 0 ]
-----------
[ _ _ 1 _ ]

=>

[]

Direct Solution Retrieval

Use the following method to retrieve solutions from the satoku matrix avoiding some duplicate solutions.

Choose one of the longest partial assignments in the intersecting region of the core problem and the variable region and convert it to a clause vector ( s_1₀ ):

[ 0 1 _ _ ]
-----------
[ 1 1 _ _ ]
[ 0 _ 1 _ ]
[ _ 1 _ 0 ]

=>

[]

Since there are no remaining clauses, every clause is satisfied. Therefore, this is also a regular minimal solution.

Now disable this selection in the matrix to avoid duplicate assignments:

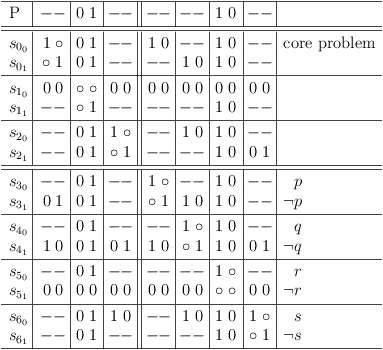
Now disable this selection in the matrix to avoid duplicate assignments

Choose the next longest partial assignment, e.g. s_2₁ :

[ _ _ 1 0 ]
-----------
[ 1 1 _ _ ]
[ 0 _ 1 _ ]
[ _ 1 _ 0 ]

=>

[ 1 1 _ _ ]

Only one clause remains, which can be satisfied either way.

Now disable this selection in the matrix and remove redundant selection rows/clauses:

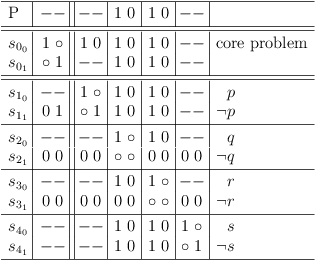
Without any conflicts, use the global problem status as solution

If the core problem section does not present any conflicts ( s_0₁ ), the global problem status can be used as sole solution:

[ _ 1 1 _ ]
-----------
[ 1 1 _ _ ]
[ 0 _ 1 _ ]
[ _ 1 _ 0 ]

=>

[]

Verification of Partial Assignments

Map a set of disjunctive clauses from a CNF problem to a set of disjunctive problem clause vectors, where a column stands for a variable.

If a variable appears unnegated in a clause, set the value in the corresponding clause vector column to 1.
If a variable appears negated in a clause, set the value in the corresponding clause vector column to 0.
If a variable does not appear negated in a clause, set the value in the corresponding clause vector column to `_´.

If a column value is set to 0 or 1, it is assigned. If a column value is set to `_´ it is not assigned.

The complement of 0 is 1 and the complement of 1 is 0. The complement of `_´ is again `_´.

Example for variables a0, a1, a2, a3, a4, a5, a6, a7, a8 :

[ 1 0 1 _ _ _ _ _ _ ] // OR, disjunctions
[ 1 1 0 _ _ _ _ _ _ ]
[ 0 1 1 _ _ _ _ _ _ ]
[ 0 0 0 _ _ _ _ _ _ ]
[ 0 _ _ 0 0 _ _ _ _ ]
[ 0 _ _ 1 1 _ _ _ _ ]
[ 1 _ _ 1 0 _ _ _ _ ]
[ 1 _ _ 0 1 _ _ _ _ ]
[ _ 1 _ _ _ 0 _ _ 1 ]
[ _ 0 _ _ _ 1 _ _ 1 ]
[ _ 1 _ _ _ 1 _ _ 0 ]
[ _ 0 _ _ _ 0 _ _ 0 ]
[ _ _ 0 _ _ 1 1 _ _ ]
[ _ _ 0 _ _ 0 0 _ _ ]
[ _ _ 1 _ _ 1 0 _ _ ]
[ _ _ 1 _ _ 0 1 _ _ ]
[ _ _ _ 0 _ _ _ 1 1 ]
[ _ _ _ 0 _ _ _ 0 0 ]
[ _ _ _ 1 _ _ _ 0 1 ]
[ _ _ _ 1 _ _ _ 1 0 ]
[ _ _ _ _ 0 _ 0 0 _ ]
[ _ _ _ _ 1 _ 1 0 _ ]
[ _ _ _ _ 0 _ 1 1 _ ]
[ _ _ _ _ 1 _ 0 1 _ ]
  a a a a a a a a a
  0 1 2 3 4 5 6 7 8

Partial Assignment Vector

A partial assignment vector is a clause vector representing a conjunction. Example:

[ 1 _ _ _ _ _ 1 _ 0 ] // AND, conjunction
  a a a a a a a a a
  0 1 2 3 4 5 6 7 8

Verification

Place the partial assignment vector on top of the problem clause vectors and separate them with a horizontal line.

Remove all problem clause vectors, that match a variable assignment (0 or 1) in the partial assignment vector at the top (clauses are satisfied).

Example:

[ 1 _ _ _ _ _ 1 _ 0 ] // AND, conjunction
---------------------
[ 0 1 1 _ _ _ _ _ _ ] // OR, disjunctions
[ 0 0 0 _ _ _ _ _ _ ]
[ 0 _ _ 0 0 _ _ _ _ ]
[ 0 _ _ 1 1 _ _ _ _ ]
[ _ 1 _ _ _ 0 _ _ 1 ]
[ _ 0 _ _ _ 1 _ _ 1 ]
[ _ _ 0 _ _ 0 0 _ _ ]
[ _ _ 1 _ _ 1 0 _ _ ]
[ _ _ _ 0 _ _ _ 1 1 ]
[ _ _ _ 1 _ _ _ 0 1 ]
[ _ _ _ _ 0 _ 0 0 _ ]
[ _ _ _ _ 1 _ 0 1 _ ]
  a a a a a a a a a
  0 1 2 3 4 5 6 7 8

For each assigned variable in the partial assignment vectors, remove the complementary assignment from each problem clause vector, by setting the corresponding column to `_´ (satisfying variable assignment is impossible).

Example:

[ 1 _ _ _ _ _ 1 _ 0 ] // AND, conjunction
---------------------
[ _ 1 1 _ _ _ _ _ _ ] // OR, disjunctions
[ _ 0 0 _ _ _ _ _ _ ]
[ _ _ _ 0 0 _ _ _ _ ]
[ _ _ _ 1 1 _ _ _ _ ]
[ _ 1 _ _ _ 0 _ _ _ ]
[ _ 0 _ _ _ 1 _ _ _ ]
[ _ _ 0 _ _ 0 _ _ _ ]
[ _ _ 1 _ _ 1 _ _ _ ]
[ _ _ _ 0 _ _ _ 1 _ ]
[ _ _ _ 1 _ _ _ 0 _ ]
[ _ _ _ _ 0 _ _ 0 _ ]
[ _ _ _ _ 1 _ _ 1 _ ]
  a a a a a a a a a
  0 1 2 3 4 5 6 7 8

Required Variable Assignments, Contradiction

If a conjunctive clause is reduced to a single assigned variable, set the corresponding column of the partial assignment vector to that value (required assignment). If the column in the partial assignment vector already contains the complementary value, the partial assignment vector is a contradiction.

If a conjunctive clause is reduced, such that no variables are assigned, the partial assignment vector is a contradiction.

Arbitrary Variable Assignment

If there are still unsatisfied problem clause vecotrs left, but no problem clause vector contains a single value, arbitrarily choose a variable assignment from any problem clause vector and add it to the partial assignment vector.

It is important, that the variable assignment must be chosen from the problem clause vectors. It is not allowed to arbitrarily choose a variable assignment, that does not satisfy any clause!

Example:

Choose a3 = 0 and proceed

[ 1 _ _ 0 _ _ 1 _ 0 ] // AND, conjunction
---------------------
[ _ 1 1 _ _ _ _ _ _ ] // OR, disjunctions
[ _ 0 0 _ _ _ _ _ _ ]
[ _ _ _ 0 0 _ _ _ _ ]
[ _ _ _ 1 1 _ _ _ _ ]
[ _ 1 _ _ _ 0 _ _ _ ]
[ _ 0 _ _ _ 1 _ _ _ ]
[ _ _ 0 _ _ 0 _ _ _ ]
[ _ _ 1 _ _ 1 _ _ _ ]
[ _ _ _ 0 _ _ _ 1 _ ]
[ _ _ _ 1 _ _ _ 0 _ ]
[ _ _ _ _ 0 _ _ 0 _ ]
[ _ _ _ _ 1 _ _ 1 _ ]
  a a a a a a a a a
  0 1 2 3 4 5 6 7 8

Then proceed with the verification process.

Satisfying Assignment

If no problem clause vectors are left (all clauses are satisfied), the partial assignment vector is a satisfying assignment for the original CNF problem. It is called a solution to the problem.

Example:

[ 1 _ _ 0 1 _ 1 0 0 ] // AND, conjunction
---------------------
[ _ 1 1 _ _ _ _ _ _ ] // OR, disjunctions
[ _ 0 0 _ _ _ _ _ _ ]
[ _ 1 _ _ _ 0 _ _ _ ]
[ _ 0 _ _ _ 1 _ _ _ ]
[ _ _ 0 _ _ 0 _ _ _ ]
[ _ _ 1 _ _ 1 _ _ _ ]
  a a a a a a a a a
  0 1 2 3 4 5 6 7 8

Choose a2 = 1 and proceed

[ 1 0 1 0 1 0 1 0 0 ] // AND, conjunction
---------------------
  a a a a a a a a a
  0 1 2 3 4 5 6 7 8

Minimal, Sub-Minimal, Micromal Solutions

If it is not possible to remove a variable assignment from a solution so that still all clauses are satisfied, the solution is called minimal. Distributive expansion of a CNF delivers a DNF with all minimal solutions.

If it is impossible to derive a contradiction from a solution and a non-empty set of problem clause vectors, the solution is called sub-minimal.

If it is not possible to remove a variable assignment from a solution, without allowing derivation of a contradiction, the solution is called micromal.

The initial solution is micromal for the above example:

[ 1 _ _ _ _ _ 1 _ 0 ] // initial solution (AND)
  a a a a a a a a a
  0 1 2 3 4 5 6 7 8

E.g., if a0 is removed from the initial solution:

[ _ _ _ _ _ _ 1 _ 0 ] // a0 removed
  a a a a a a a a a
  0 1 2 3 4 5 6 7 8

it is possible to derive a contradiction:

Choose a0 = 0 and proceed

[ 0 _ _ _ _ _ 1 _ 0 ] // AND, conjunction
---------------------
[ _ 0 1 _ _ _ _ _ _ ] // OR, disjunctions
[ _ 1 0 _ _ _ _ _ _ ]
[ _ _ _ 1 0 _ _ _ _ ]
[ _ _ _ 0 1 _ _ _ _ ]
[ _ 1 _ _ _ 0 _ _ _ ]
[ _ 0 _ _ _ 1 _ _ _ ]
[ _ _ 0 _ _ 0 _ _ _ ]
[ _ _ 1 _ _ 1 _ _ _ ]
[ _ _ _ 0 _ _ _ 1 _ ]
[ _ _ _ 1 _ _ _ 0 _ ]
[ _ _ _ _ 0 _ _ 0 _ ]
[ _ _ _ _ 1 _ _ 1 _ ]
  a a a a a a a a a
  0 1 2 3 4 5 6 7 8

Choose a1 = 0 and proceed

[ 0 0 0 _ _ 0 1 _ 0 ] // AND, conjunction
---------------------
[ _ _ _ 1 0 _ _ _ _ ] // OR, disjunctions
[ _ _ _ 0 1 _ _ _ _ ]
[ _ _ _ _ _ _ _ _ _ ] // CONTRADICTION
[ _ _ _ 0 _ _ _ 1 _ ]
[ _ _ _ 1 _ _ _ 0 _ ]
[ _ _ _ _ 0 _ _ 0 _ ]
[ _ _ _ _ 1 _ _ 1 _ ]
  a a a a a a a a a
  0 1 2 3 4 5 6 7 8

Copyright