Prime Implicants And Reliable Assignments
| Author: | Wolfgang Scherer |
|---|
Contents
Observation: All prime implicants are a conjunction of elements from a special set of partial assignments A . Although these partial assignments are not necessarily implicants, they are reliable, since a refinement function R exists which only generates implicants. I.e., R never generates unsatisfying assignments from a reliable assignment r.
Rationale: For the special case of 2-SAT problems, the set of reliable assignments defining the prime implicants can be generated much more efficiently with a worst case upper bound of O(n2) than the set of prime implicants, which has a worst case upper bound of O(2n) .
Theory: Asking for a set of implicants representing all solutions to a propositional problem overspecifies the requirements. I.e., it is sufficient to provide a set of implicants, but it is not necessary. Providing a set of reliable assignments is sufficient and necessary to represent all solutions of a propositional formula.
Lemma: It is not necessary to generate a fully satisfying assignment to show satisfiability. Presenting a reliable assignment r and the polynominal time reliable refinement function R is sufficient.
A satisfying assignment C for the generally accepted verfication function V can be produced in polynomial time O(poly) by refining a reliable assignment r with the reliable refinement function R over the set of clauses C .
Lemma: For certain optimization problems, e.g. W2-SAT, it is sufficient but not necessary to enumerate the entire set of solutions. It is known, that a set of prime implicants (or other sets of implicants) is sufficient to represent all solutions. Generating such a set of implicants has a worst case upper bound of O(2m) over the number of clauses C , with m = |C| . With the set of reliable implicants, the worst case upper bound can be reduced to O((m + v)2) , where v is the number of variables.
Note, that the set of reliable assignments can provide a good estimate for the total number of solutions. However, giving an exact count for all solutions is still bound by the worst case running time of O(2u) over the set of remaining unsatisfied clauses U , with u = |U| , for each reliable assignment. Therefore #SAT holds and this algorithm does not violate it.
Base Problem
|:todo:| The example is not the best one, it should be replaced by a better one.
Propositional forumula:
( ¬a ∨ ¬b ) ∧ ( ¬a ∨ d ) ∧ ( a ∨ b ) ∧ ( a ∨ c ) ∧ ( ¬b ∨ c ) ∧ ( b ∨ d ) ∧ ( c ∨ d )
Clause vectors:
[ 0 0 _ _ ] [ 0 _ _ 1 ] [ 1 1 _ _ ] [ 1 _ 1 _ ] [ _ 0 1 _ ] [ _ 1 _ 1 ] [ _ _ 1 1 ] a b c d
Prime implicants:
( ¬a ∧ b ∧ c ) ∨ ( a ∧ ¬b ∧ d ) [ 0 1 1 _ ] [ 1 0 _ 1 ] a b c d
Reliable Assignments
A reliable assignment r over the clauses C of a propositional problem in CNF is determined by the following reliable refinement function R , which returns the set of all assignments defined by r or an empty set, if r is not a reliable assignment.
The steps are defined in order of highest priority to lowest priority. If a higher priority step fails, the next lower priority step is attempted. When a step is completed, evaluation starts again with the highest priority step (not with the next step!). The procedure is repeated until C becomes emtpy and the result set S is returned.
- If C is empty then return S .
- If C contains an empty clause, a contradiction is found. It follows that r is not a reliable assignment. An exception is thrown and at top-level an empty set is returned.
- Remove all clauses from C which are satisfied by r . If C becomes empty, add the current assignment defined by r to the result set S .
- Remove all literals from clauses in C , which conflict with r .
- If C contains a clause X with exactly one literal l and r already contains the conflicting literal ¬l , remove l from clause X . Otherwise refine r by adding l .
- Choose an arbitary literal l (which was not already chosen) from any clause X in C . If r already contains ¬l , remove all literals from X . Otherwise remember the state for backtracking, refine r with l and continue recursively. Return from backtracking: Restore the state and repeat step 6.
Note: Steps 3, 4 and 5 are equivalent to the unit-clause-rule of DPLL. The empty clause corresponds to the unsatisfiabilty condition of the resolution process.
An assignment r is said to be reliable, if the reliable assignment function R(r) returns a non-empty set of assignments. If the result set is empty, assignment r is not reliable.
An assignment e is said to reliably extend a reliable assignment r , if e is element of R(r) . e is said to be a reliable refinement of r .
A reliable assignment r is said to refine reliably to an assignment e , if e is element of R(r) .
Reliable assignments for the base problem:
[ 0 1 1 _ ] reliable assignment, also prime implicant [ 1 0 _ 1 ] reliable assignment, also prime implicant [ _ _ 1 _ ] reliable assignment, but not prime implicant [ _ _ _ 1 ] reliable assignment, but not prime implicant
Proof is done by following all branches of the reliable refinement function:
Remove satisfied clauses:
[ _ _ 1 _ ] reliable assignment, but not prime implicant ----------- [ 0 0 _ _ ] [ 0 _ _ 1 ] [ 1 1 _ _ ] [ _ 1 _ 1 ] a b c d
A branch occurs, when there is no neccessary assignment present in the clauses. In this case, assign an arbitrary variable, so that a literal from one of the clauses becomes true. I.e., in this example d = 1 is allowed, d = 0 is not allowed:
[ _ 0 1 _ ] refined assignment ----------- [ 0 0 _ _ ] [ 0 _ _ 1 ] [ 1 1 _ _ ] [ _ 1 _ 1 ] a b c d
Remove satisfied clauses:
[ _ 0 1 _ ] ----------- [ 0 _ _ 1 ] [ 1 1 _ _ ] [ _ 1 _ 1 ] a b c d
Remove conflicting literals from clauses:
[ _ 0 1 _ ] ----------- [ 0 _ _ 1 ] [ 1 _ _ _ ] // single literal must be assigned [ _ _ _ 1 ] // single literal must be assigned a b c d
Assign next required literal from clauses, where only one literal is left:
[ 1 0 1 _ ] ----------- [ 0 _ _ 1 ] [ 1 _ _ _ ] // single literal must be assigned [ _ _ _ 1 ] // single literal must be assigned a b c d
Remove satisfied clauses:
[ 1 0 1 _ ] ----------- [ 0 _ _ 1 ] [ _ _ _ 1 ] a b c d
Remove conflicting literals from clauses:
[ 1 0 1 _ ] ----------- [ _ _ _ 1 ] [ _ _ _ 1 ] a b c d
Assign next required literal from clauses, where only one literal is left:
[ 1 0 1 1 ] ----------- [ _ _ _ 1 ] [ _ _ _ 1 ] a b c d
Remove satisfied clauses:
[ 1 0 1 1 ] solution ----------- a b c d
If all clauses can be removed, the assignment is satisfying.
Why (a , b, c, d) is not a valid reliable refinement of (c)
Argument: The target assignment (a, b, c, d) is not a satisfying assignment for the problem, therefore (c) is not a reliable assignment:
[ 1 1 1 1 ]
Since (a, b, c, d) extends (c), and (c) refines to (a, b, c, d), it could be argued, that (c) is not reliable. However, if (c) shall be proven unreliable, (a, b, c, d) must be reliably refinable from (c).
The reliable refinement function R is strictly defined and cannot be circumvented after the fact, nor can it be replaced by any other function.
It specifies, that each assignment, that is refinable from a reliable assignment r by following the provisions of the reliable refinement function R must be a satisfying assignment for the problem. No statement is made about other possible assignments that extend a reliable assignment r in other ways.
If an arbitrary assignment e is assumed to be a reliable refinement of a reliable assignment r , it must be proved that R(r) produces said assignment e.
For the assignment (a, b, c, d) it can be shown, that it does not reliably extend the reliable assignment (c).
Try a=1 For Reliable Refinement
Try to refine reliable assignment (c) to unsatisfying target assignment (a, b, c, d):
[ _ _ 1 _ ] reliable assignment, but not prime implicant ----------- [ 0 0 _ _ ] [ 0 _ _ 1 ] [ 1 1 _ _ ] [ _ 1 _ 1 ] a b c d
Arbitrarily choose a=1 from the target assignment for refinement:
[ 1 _ 1 _ ] ----------- [ 0 0 _ _ ] [ 0 _ _ 1 ] [ 1 1 _ _ ] [ _ 1 _ 1 ] a b c d
Remove satisfied clauses:
[ 1 _ 1 _ ] ----------- [ 0 0 _ _ ] [ 0 _ _ 1 ] [ _ 1 _ 1 ] a b c d
Remove conflicting literals from clauses:
[ 1 _ 1 _ ] ----------- [ _ 0 _ _ ] [ _ _ _ 1 ] [ _ 1 _ 1 ] a b c d
Assign next required literal:
[ 1 0 1 _ ] ----------- [ _ _ _ 1 ] [ _ 1 _ 1 ] a b c d
Remove conflicting literals from clauses:
[ 1 0 1 _ ] ----------- [ _ _ _ 1 ] [ _ _ _ 1 ] a b c d
Assign next required literal:
[ 1 0 1 1 ] ----------- [ _ _ _ 1 ] [ _ _ _ 1 ] a b c d
Remove satisfied clauses:
[ 1 0 1 1 ] ----------- a b c d
Try b=1 for Reliable Refinement
Try again to refine reliable assignment (c) to unsatisfying target assignment (a, b, c, d):
[ _ _ 1 _ ] reliable assignment, but not prime implicant ----------- [ 0 0 _ _ ] [ 0 _ _ 1 ] [ 1 1 _ _ ] [ _ 1 _ 1 ] a b c d
Choose b=1:
[ _ 1 1 _ ] ----------- [ 0 0 _ _ ] [ 0 _ _ 1 ] [ 1 1 _ _ ] [ _ 1 _ 1 ] a b c d
Remove satisfied clauses:
[ _ 1 1 _ ] ----------- [ 0 0 _ _ ] [ 0 _ _ 1 ] a b c d
Remove conflicting literals from clauses:
[ _ 1 1 _ ] ----------- [ 0 _ _ _ ] [ 0 _ _ 1 ] a b c d
Assign next required literal:
[ 0 1 1 _ ] ----------- [ 0 _ _ _ ] [ 0 _ _ 1 ] a b c d
Remove satisfied clauses:
[ 0 1 1 _ ] ----------- a b c d
Try d=1 For Reliable Refinement
Try again to refine reliable assignment (c) to unsatisfying target assignment (a, b, c, d):
[ _ _ 1 _ ] reliable assignment, but not prime implicant ----------- [ 0 0 _ _ ] [ 0 _ _ 1 ] [ 1 1 _ _ ] [ _ 1 _ 1 ] a b c d
Arbitrarily choose d=1 for refinement (d=0 would not be allowed!):
[ _ _ 1 1 ] ----------- [ 0 0 _ _ ] [ 0 _ _ 1 ] [ 1 1 _ _ ] [ _ 1 _ 1 ] a b c d
Remove satisfied clauses:
[ _ _ 1 1 ] ----------- [ 0 0 _ _ ] [ 1 1 _ _ ] a b c d
Arbitrarily choose a=1 for assignment:
[ 1 _ 1 1 ] ----------- [ 0 0 _ _ ] [ 1 1 _ _ ] a b c d
Remove satisfied clauses:
[ 1 _ 1 1 ] ----------- [ 0 0 _ _ ] a b c d
Remove conflicting literals from clauses:
[ 1 _ 1 1 ] ----------- [ _ 0 _ _ ] a b c d
Assign next required literal:
[ 1 0 1 1 ] ----------- [ _ 0 _ _ ] a b c d
Remove satisfied clauses:
[ 1 _ 1 1 ] ----------- a b c d
It should be clear, that the assignment (a, b, c, d) cannot be reliably refined from the reliable assignment (c). The fact that (a, b, c, d) extends (c) has no bearing on the reliability of (c) as long as it does not reliably extend (c).
It should also be clear, that it is sufficient to try once. If that does not work, there is no other way.
|:todo:| think of a nice proof
Other Reliable Assignments
If an assignment does not appear as literal in the CNF clauses, it can still be reliable.
[ _ _ 0 _ ] reliable assignment ----------- [ 0 0 _ _ ] [ 0 _ _ 1 ] [ 1 1 _ _ ] [ 1 _ 1 _ ] [ _ 0 1 _ ] [ _ 1 _ 1 ] [ _ _ 1 1 ] a b c d
[ _ _ 0 _ ] reliable assignment ----------- [ 0 0 _ _ ] [ 0 _ _ 1 ] [ 1 1 _ _ ] [ 1 _ _ _ ] [ _ 0 _ _ ] [ _ 1 _ 1 ] [ _ _ _ 1 ] a b c d
[ 1 0 0 1 ] reliable assignment ----------- [ 0 0 _ _ ] [ 0 _ _ 1 ] [ 1 1 _ _ ] [ 1 _ _ _ ] [ _ 0 _ _ ] [ _ 1 _ 1 ] [ _ _ _ 1 ] a b c d
[ 1 0 0 1 ] reliable assignment ----------- a b c d
Unreliable assignment
This unreliable assignment is also a nogood, guaranteed to produce no statisfying assignment.
Unfortunately this example does not contain a simple ambiguous assignment, which allows to produce both satisfying and unsatisfying assignments.
[ 0 0 _ _ ] nogood ----------- [ 0 0 _ _ ] [ 0 _ _ 1 ] [ 1 1 _ _ ] [ 1 _ 1 _ ] [ _ 0 1 _ ] [ _ 1 _ 1 ] [ _ _ 1 1 ] a b c d
[ 0 0 _ _ ] nogood ----------- [ 1 1 _ _ ] [ 1 _ 1 _ ] [ _ 0 1 _ ] [ _ 1 _ 1 ] [ _ _ 1 1 ] a b c d
[ 0 0 _ _ ] nogood ----------- [ _ _ _ _ ] // contradiction! [ _ _ 1 _ ] [ _ 0 1 _ ] [ _ _ _ 1 ] [ _ _ 1 1 ] a b c d
Relation to Satoku Matrix
Proof of Reliability for 2-SAT
Try to construct a reliable assignment r that allows a contradiction.
1. If a reliable assignment r is an implicant, no contradiction is possible. Therefore there must be a prime implicant pr that extends r .
2. The reliable assignment rc must extend r and must allow a contradiction.
3. If rc extends or is equivalent to any prime implicant p , a contradiction is not possible, otherwise p would not be a prime implicant.
Therefore rc must conflict with all prime implicants pn that do not conflict with r . This implies that rc extends a literal lc , such that r does not extend lc . lc must conflict with all prime implicants pn .
4. To trigger the contradiction, there must be a clause cc , with two alternatives: a literal l0 that conflicts with r and the literal lc .
5. Any partial assignment sr which requires r will conflict with l0 and will therefore require lc . Due to partial distributive expansion, all sr will be updated to require both r and lc .
This implies a prime implicant pc so that rc extends pc . Therefore, condition 3 is no longer satisfied and rc cannot cause a contradiction.
QED
Example
Satoku matrix redundancies removed
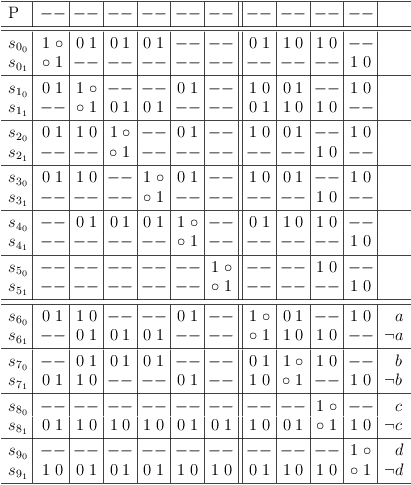
Satoku matrix redundancies removed
Distributive expansion of S0, .., S5 , redundancies removed
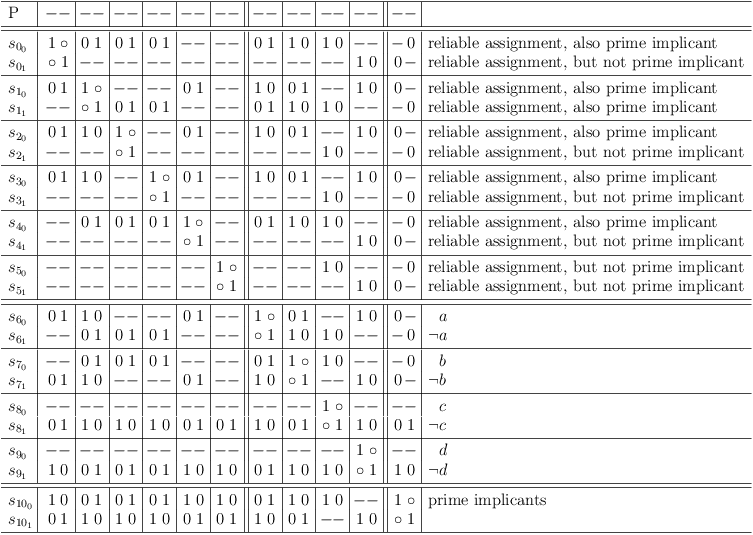
Distributive expansion, redundancies removed
Relation to Other SAT Problems
|:todo:| THIS iS WORK IN PROGRESS. PLEASE SKIP IT.
MAX-2-SAT:
Is there an assignment that satisfies at least K of the clauses.
can be expressed as:
Is there a k-tuple (at least k) of non-conflicting reliable assignments for a 2-CNF formula.
|:todo:| It is equivalent to asking, whether a satisfiable k-SAT instance can be derived from the vertex cover problem.
The conjunction of k reliable assignments results in a reliable assignment r , so that any implicant refined from r with the reliable refinement function R complies with the condition. A satisfying assignment can then be produced from the implicant.
Note, that this requires that redundant clauses are not removed from the satoku matrix. Also, duplicate reliable assignments cannot be eliminated. This would result in a set with multiple occurences of reliable assignments. Since it is not a set in the narrow sense of the definition, the following modification allows to ceate an appropriate set for R .
The duplicate instances of reliable assignments are counted and a set can be produced, that associates a count with a unique reliable assignment:
{ (r_0, 5), (r_1, 7), ... }The question is then modified to:
Is there a non-conflicting conjunction of reliable assignments, whose sum of occurrences is at least k?
(r_0, 5) (r_1, 7) (r_2, 20) (r_3, 1) (r_4, 6) \ / \ / \ / \ / \ / \ / \ / \ / (r, 12) (r, 27) (r, 23) (r, 7) r_0 & !r_1 r_2 & !r_3 r_1 & !r_4 5 0 26 6 0 0 7 33 15 13 20 0 26 0 1 7 0 6
W2SAT can be expressed as:
Is there a reliabe assignment, which can be refined such that at most k of the variables are true.
This is best solved with the related vertex cover problem.
Definition of SAT Problems
MAX-2-SAT
Now consider the problem of, given a 2-CNF formula, maximize the number of clauses satisfied.
To better analyze this problem we translate it into a decision problem. We add to the input a threshold K, and simply ask whether there exists an assignment that satisfies at least K of the clauses. We call this problem Max-2-SAT.
http://en.wikipedia.org/wiki/MAX-2SAT#Maximum-2-satisfiability
In the maximum-2-satisfiability problem (MAX-2-SAT), the input is a formula in conjunctive normal form with two literals per clause, and the task is to determine the maximum number of clauses that can be simultaneously satisfied by an assignment. MAX-2-SAT is NP-hard and it is a particular case of a maximum satisfiability problem.
By formulating MAX-2-SAT as a problem of finding a cut (that is, a partition of the vertices into two subsets) maximizing the number of edges that have one endpoint in the first subset and one endpoint in the second, in a graph related to the implication graph, and applying semidefinite programming methods to this cut problem, it is possible to find in polynomial time an approximate solution that satisfies at least 0.940... times the optimal number of clauses.[35] A balanced MAX 2-SAT instance is an instance of MAX 2-SAT where every variable appears positively and negatively with equal weight. For this problem, one can improve the approximation ratio to min left{(3 - cos theta)^{-1} (2 + (2/pi)theta) ,:, pi/2 leq theta leq pi right} = 0.943....
If the unique games conjecture is true, then it is impossible to approximate MAX 2-SAT, balanced or not, with an approximation constant better than 0.943... in polynomial time.[36] Under the weaker assumption that P ≠ NP, the problem is only known to be inapproximable within a constant better than 21/22 = 0.95454...[37]
Various authors have also explored exponential worst-case time bounds for exact solution of MAX-2-SAT instances.[38]
Weighted-2-satisfiability
http://en.wikipedia.org/wiki/MAX-2SAT#Weighted-2-satisfiability
In the weighted 2-satisfiability problem (W2SAT), the input is an n-variable 2SAT instance and an integer k, and the problem is to decide whether there exists a satisfying assignment in which at most k of the variables are true. One may easily encode the vertex cover problem as a W2SAT problem: given a graph G and a bound k on the size of a vertex cover, create a variable for each vertex of a graph, and for each edge uv of the graph create a 2SAT clause u ∨ v. Then the satisfying instances of the resulting 2SAT formula encode solutions to the vertex cover problem, and there is a satisfying assignment with k true variables if and only if there is a vertex cover with k vertices. Therefore, W2SAT is NP-complete.
Moreover, in parameterized complexity W2SAT provides a natural W[1]-complete problem,[39] which implies that W2SAT is not fixed-parameter tractable unless this holds for all problems in W[1]. That is, it is unlikely that there exists an algorithm for W2SAT whose running time takes the form f(k)·nO(1). Even more strongly, W2SAT cannot be solved in time no(k) unless the exponential time hypothesis fails.[40]
DPLL
Handbook of Satisfiablitiy, p. 19.
The notion of concensus was rediscovered by Samson and Mills [SM54] (1954) and Quine [Qui55] (1955). Later, Quine [Qui59] (1959) and McCluskey [McC59] (1959) provided a systematic method for the minimization of DNF expressions through the notion of essential prime implicants (necessary prime implicants) by turning the 2-level minimization problem into a covering problem. This was perhaps the first confrontation with complexity issues: although they did not know it at the time, the problem they were trying to solve is NP-complete and the complexity of their algorithm was O(3^n/√n), where n is the number of variables.
DPLL
Handbook of Satisfiablitiy, p. 20.
The one literal rule also known as the unit-clause-rule: for each clause (l), called a unit clause, remove all clauses containing l and all literals ¬l.
The affirmative-negative rule also known as the pure-literal-rule: if literal l is in some clause but ¬l is not, remove all clauses containing l. Literal l is called a pure literal .
The rule for eliminating atomic formulas: that is, replace
(p ∨ l1,1 ∨ . . . ∨ l1,k1 ) ∧ (¬p ∨ l2,1 ∨ . . . ∨ l2,k2 ) ∧ C
with
(l1,1 ∨ . . . ∨ l1,k1 ∨ l2,1 ∨ . . . ∨ l2,k2 ) ∧ C
if literals l1,i and l2,j are not complementary for any i, j.
The splitting rule, called in the manuscript ‘the rule of case analysis.’
Frequently Asked Questions
| Q: | Why is it so important that a reliable assignment should be acceptable as a certificate for satisfiability? Can't you just generate a total assignment? |
|---|---|
| A: | The satisfiability problem requires, that the certificate for statisfiability C given by an algorithm L for a propositional problem P , must be verifyable by a function V in polynomial time O(V(C, P)) = O(poly) for all P, C exists V: C = L(P) and O(V(C, P)) = O(poly) => V is a polynomial time verfication function => C is acceptable as input for V Usually this is interpreted as:
C := total assignment of variables
V_f(C, P):= evaluate P with the truth values of the
variables defined by C and
verify that the result is TRUE
Example:
V = V_f
C = ((a, T), (b, F), (c, F))
P = (a ∨ ¬b) ∧ (b ∨ ¬c)
V(C, P) => (T ∨ T) ∧ (F ∨ T)
= T ∧ T
= T
In this case, not even an implicant is acceptable as certificate. Defining certificates as implicants and a verfication function Vi as: C := implicant V_i(C, P) := set all unassigned variables of C to FALSE, return V_f(C, P) allows implicants (as well as total assignments) as certificates:
V = V_i
C = ((a, T), (c, F))
P = (a ∨ ¬b) ∧ (b ∨ ¬c)
V(C, P) => (T ∨ T) ∧ (F ∨ T)
= T ∧ T
= T
Using reliable assignments r as certificate and the verification function Vr based on the reliable refinement function R , which produces an implicant from r in polynomial time is also sufficient: C := reliable assignment V_r(C, P) := V_i(R(C, P), P) Example:
V = V_r
C = ((c, T))
P = ( ¬a ∨ b ∨ c ) ∧ ( a ∨ ¬b ∨ d )
R(C, P) => ((a, T), (b, F), (c, T), (d, T))
V(C, P) => (F ∨ F ∨ T) ∧ (T ∨ T ∨ T)
= T ∧ T
= T
For all I know (which is not very exhaustive), refinement of partial assignments is basically some educated guesswork. Satisfiability is detected, when all clauses are satisfied, which may or may not result in a partial assignment. These implicants are pretty much random and have no well-defined properties in relation to other implicants. So there is not much difference in presenting an implicant or a total assignment as certificate. Producing a total assignment as certificate for satisfiability makes the algorithm L and the refinement function R a black box. And if it were just for satisfiability, that would be fine. However, perfectly good assignments are very useful on their own, even more so than prime implicants, and I wish to use them in other contexts (e.g. MAX-2-SAT). Since they appear as input there, they would have to be explained again and again, which just does not make any sense. |
Copyright
Copyright (C) 2013, Wolfgang Scherer, <Wolfgang.Scherer@gmx.de>. See the document source for conditions of use under the GNU Free Documentation License.