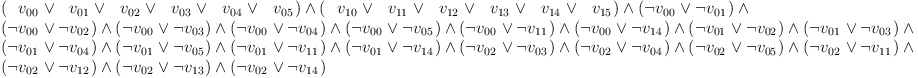1. Satoku Matrix¶
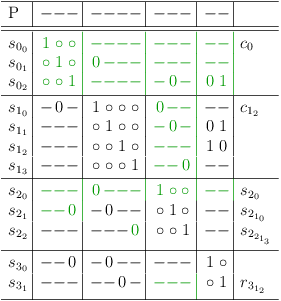
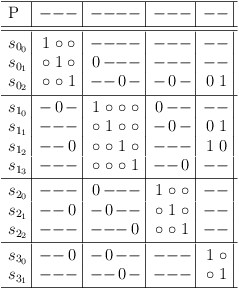
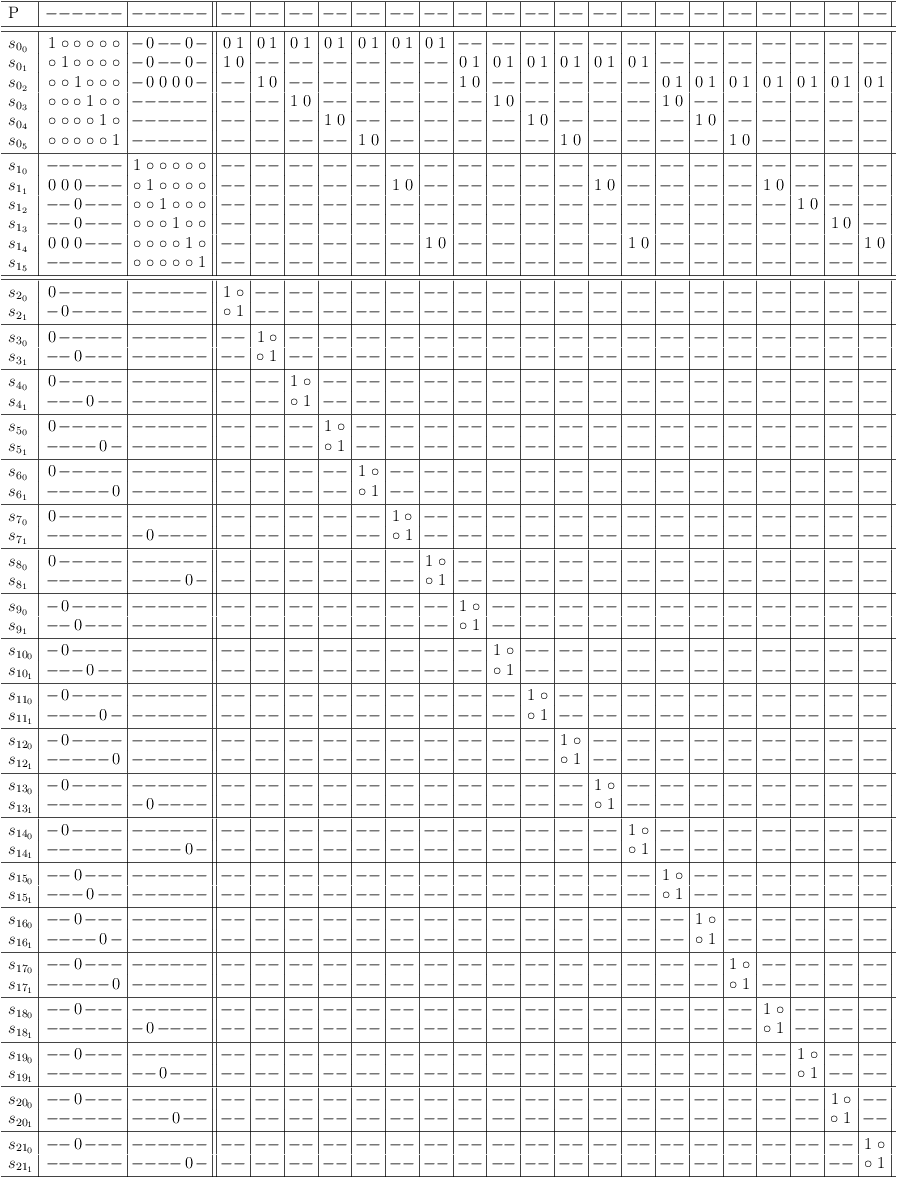
A satoku matrix is an inverted adjacency matrix preserving clause boundary information for implementing a requirement update algorithm (see figure 1.3).
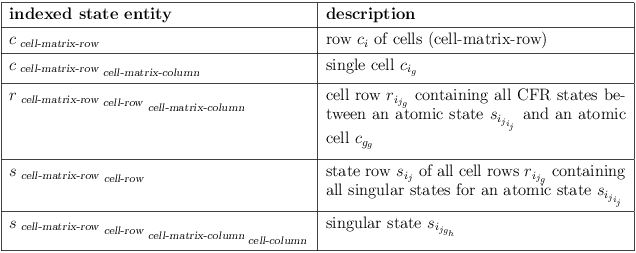
A satoku matrix \(\mathbb{S}\) is formally defined as a sequence of cell-matrix rows \(c_{i},\; 0 \le i < |\mathbb{S}|\), where a \(\mbox{\it cell-matrix row}\) \(c_i\) consists of cells \(c_{i_g},\: 0 \le g < |\mathbb{S}|\). A cell \(c_{i_g}\) consists of cell rows \(r_{i_{j_g}},\; 0 \le j < |c_{i_g}|\), where a cell row \(r_{i_{j_g}}\) consists of states \(s_{i_{j_{g_h}}},\; 0 \le h < |r_{i_{j_g}}|\). A state \(s_{i_{j_{g_h}}}\) represents a conflict relationship CFR with the state \(s_{g_{h_{i_j}}}\), where a conflict relationship is either \(\mbox{\it possible} = 1\) or \(\mbox{\it impossible} = 0\). A state row \(s_{i_j},\; 0 \le j < |c_{i_i}|\) is the sequence of cell rows \(r_{i_{j_g}}\). The index scheme is summarized in table 1.1.
|
For better readability, if a cell row \(r_{i_{j_g}}\) contains more than one 1-state, all 1-states in \(r_{i_{j_g}}\) are represented by a dash (-) (see figure 1.1).
figure 1.1 Satoku Matrix Index Scheme Example
Merging a sequence of state rows \(S\) into a state row \(s_{i_j}\), denoted as \(\mathbf{Mrg}(s_{i_j}, S)\), is defined by the algorithm in figure 1.2. It returns the number of \(1 \rightarrow 0\) transitions performed.
figure 1.2 Merge State Rows \(S\) Into State Row \(s_{i_j}\)¶
The requirement update algorithm in figure 1.3 distributes conflict relationships into all cell rows which have a single 1-state. After applying the requirement update algorithm, the satoku matrix \(\mathbb{S}\) is called consolidated.
figure 1.3 Requirement Update Algorithm¶
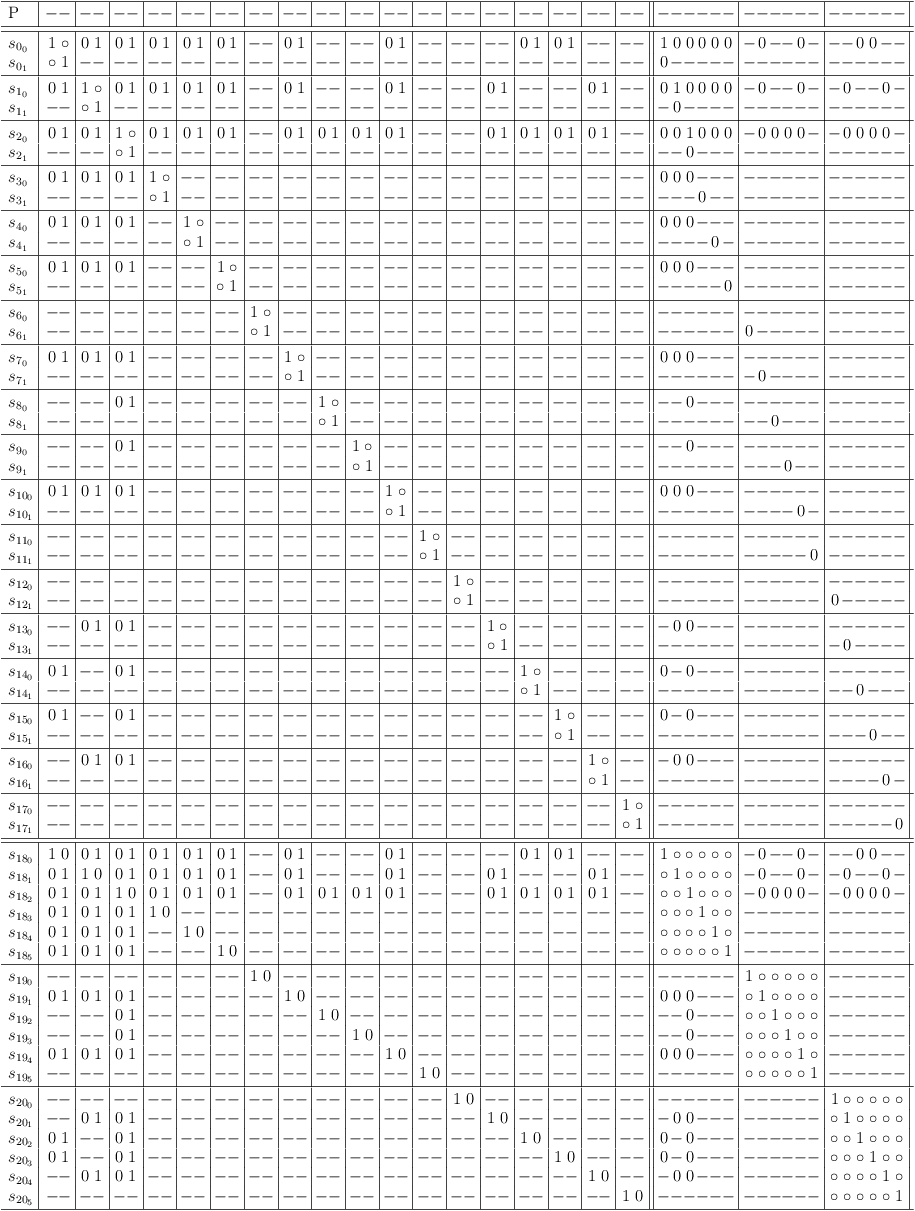
The consolidated version of the Satoku Matrix Index Scheme Example from figure 1.1 is shown in figure 1.4. Notably \(s_{0_{2_{3_1}}}\) triggered a merge of \(s_{3_1}\) into \(s_{0_2}\). This led to state \(s_{3_{1_{1_2}}}\) causing \(1 \rightarrow 0\) transitions of state \(s_{0_{2_{1_2}}}\) and state \(s_{1_{2_{0_2}}}\).
figure 1.4 Consolidated Satoku Matrix Index Scheme Example
2. Mapping a CNF Formula to a Satoku Matrix¶
A CNF formula \(F\) is a conjunction of \(m\) disjunctive clauses \(C_i\) each containing \(k_i\) literals \(l_j\), where a literal \(l_j\) is a negated or unnegated boolean variable:
Mapping a CNF formula \(F\) to a satoku matrix \(\mathbb{S}\) with the algorithm in figure 2.1 results in an unconsolidated satoku matrix \(\mathbb{S}\).
figure 2.1 Mapping a CNF Formula to a Satoku Matrix¶
3. Mapping a Satoku Matrix to a CNF Formula¶
See figure 3.1 for an algorithm to map a satoku matrix to a CNF formula.
figure 3.1 Mapping a Satoku Matrix to a CNF Formula¶
4. Initial Information Encoding¶
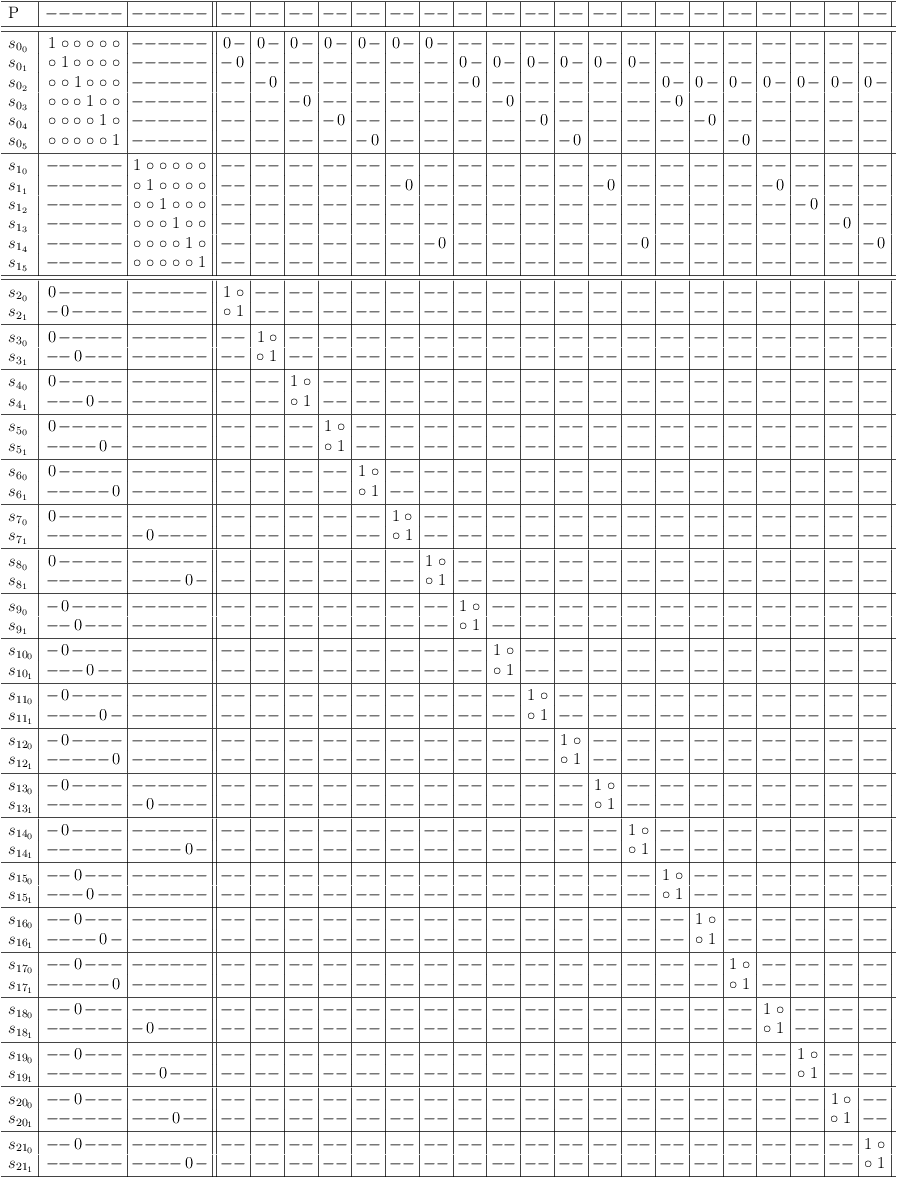
Arbitrary pixel blocks like “HAPPYEASTER!<smile><egg><egg>” can be encoded in the upper right half of a satoku matrix in a simple manner by flipping 1-states to 0 (see figure 4.1).
figure 4.1 Text Encoded in a Satoku Matrix
The satoku matrix in figure 4.1 can then be mapped to CNF formula (see figure 6.1). Since this formula is huge, only a reduced version is shown here in figure 4.2.
figure 4.2 Reduced CNF Formula of Mapped Satoku Matrix
Mapping the CNF formula in figure 4.2 to an unconsolidated satoku matrix, effectively hides the encoded information (see figure 4.3).
figure 4.3 Reduced CNF Formula Mapped to Unconsolidated Satoku Matrix
Performing the requirement update (figure 1.3) to the satoku matrix in figure 4.3 results in a consolidated satoku matrix, which shows the restored original information (see figure 4.4).
figure 4.4 Consolidated Satoku Matrix for Reduced CNF Formula
5. Advanced Information Hiding¶
Removing the at-least-1 clauses from the reduced CNF formula in figure 4.3 results in a set of 2-literal clauses (see figure 5.1). For the full formula in figure 6.1 without at-least-1 clauses see figure 7.1.
figure 5.1 Reduced CNF Formula Without At-Least-1 Clauses
Producing a consolidated satoku matrix from the formula in figure 5.1 lacks any information whatsoever (see figure 5.2).
figure 5.2 Consolidated Satoku Matrix for Reduced CNF Formula Without At-Least-1 Clauses
When the variables of the CNF formula in figure 5.1 are mapped via 2-literal clauses of the form \(( p \vee \neg p )\), only the conflict relationships between the clauses and variables become visible (see figure 5.3)
figure 5.3 Unconsolidated Satoku Matrix of Reduced CNF With Mapped Variables
Only when the requirement update algorithm in figure 1.3 is applied to the unconsolidated satoku matrix in figure 5.3 the information reappears in the lower right mapped variable quadrant (see figure 5.4).
figure 5.4 Consolidated Satoku Matrix of Reduced CNF With Mapped Variables
The mapped variable quadrant of the satoku matrix derived from the full CNF formula in figure 7.1 already hints strongly at the encoded message (see figure 5.5).
figure 5.5 Mapped Variable Quadrant of Full CNF Formula Without At-Least-1 Clauses
The original message can be restored by adding the at-least-1 clauses manually to the mapped variable quadrant from figure 5.4 and making exactly one mapped variable required in the lower right quadrant for each literal of the at-least-1 clauses (see figure 5.6).
figure 5.6 At-Least-1 Clauses Manually Added to Mapped Variable Quadrant
Running the requirement update algorithm from figure 1.3 consolidates the satoku matrix from figure 5.6 and restores the original message in the lower right Quadrant (see figure 5.7).
figure 5.7 Requirement Update Restores Original Message
Removing the mapped variables finally leaves an exact copy of the original message (see figure 5.8).
figure 5.8 Removing Mapped Variables Leaves Exact Copy of Original Message
6. Satoku Matrix Mapped to CNF Formula¶
figure 6.1 Satoku Matrix Mapped to CNF Formula
