Partial Distributive Expansion of CNF Problems

The Foundation of the Satoku Matrix

Author:	Wolfgang Scherer

Contents

Human Friendly Propositional Logic
Satoku Matrix

Human Friendly Propositional Logic

Propositional logic does not provide the best abstraction for the satoku matrix. In fact it is actually quite misleading. However, it is still useful to express the principle of partial distributive expansion in propositional logic, as it provides a good amount of redundancy to understand the concept.

Since it is meant as a hint only, the description is informal to avoid a duplication of efforts. I.e., nothing in this description is necessary to define the satoku matrix.

Starting with the propositional CNF formula P with m = |P| disjunctive clauses C of size k:

( ¬a ∨ ¬b ) ∧ ( ¬a ∨ d ) ∧ ( a ∨ b ) ∧ ( a ∨ c )

Convert each disjunction C of literals to a disjunction S of conjunctions s:

(( ¬a ) ∨  ( ¬b )) ∧
(( ¬a ) ∨  (  d )) ∧
((  a ) ∨  (  b )) ∧
((  a ) ∨  (  c ))

As visual hint, spread each conjunction s of each disjunction S over two lines:

(( ¬a                                    ) ∨
 (      ¬b                               )) ∧
((           ¬a                          ) ∨
 (                 d                     )) ∧
((                      a                ) ∨
 (                           b           )) ∧
((                                a      ) ∨
 (                                     c ))

Extend each conjunction s with truth values TRUE to a length of k*m in the following manner:

(( ¬a ∧  T ∧  T ∧  T ∧  T ∧  T ∧  T ∧  T ) ∨
 (  T ∧ ¬b ∧  T ∧  T ∧  T ∧  T ∧  T ∧  T )) ∧
((  T ∧  T ∧ ¬a ∧  T ∧  T ∧  T ∧  T ∧  T ) ∨
 (  T ∧  T ∧  T ∧  d ∧  T ∧  T ∧  T ∧  T )) ∧
((  T ∧  T ∧  T ∧  T ∧  a ∧  T ∧  T ∧  T ) ∨
 (  T ∧  T ∧  T ∧  T ∧  T ∧  b ∧  T ∧  T )) ∧
((  T ∧  T ∧  T ∧  T ∧  T ∧  T ∧  a ∧  T ) ∨
 (  T ∧  T ∧  T ∧  T ∧  T ∧  T ∧  T ∧  c ))

If pseudo code is preferred:

def spread_problem(P):
    PM = []
    w = sum([len(C) for C in P])
    o = 0
    for C in enumerate(P):
        d = []
        PM.append(d)
        for lit in C:
            c = [ true for i in range(w) ]
            c[o] = lit
            d.append(c)
            o += 1
    return PM

Disjunctions S are labeled Si, i = (0, 1, .., m − 1), m = |P|.
Conjunctions s are labeled sij, j = (0, 1, .., |Si| − 1).
Literals are labeled as row, column pairs sij, fg, f = (0, 1, .., m − 1), g = (0, 1, .., |Si| − 1).
Literals sij, ij are the original literals of the clause.

Matrix Representation

It is easier to work on a matrix SM, (or call it table, if you must) when performing the partial distributive expansion for partial assignments s_{i_j} representing selections of the corresponding selection problem:

---------------------+-------+-------+-------+-------+
:math:`s_{{0}_{0}}`  | ¬a    |       |       |       |
:math:`s_{{0}_{1}}`  |    ¬b |       |       |       |
---------------------+-------+-------+-------+-------+
:math:`s_{{1}_{0}}`  |       | ¬a    |       |       |
:math:`s_{{1}_{1}}`  |       |     d |       |       |
---------------------+-------+-------+-------+-------+
:math:`s_{{2}_{0}}`  |       |       |  a    |       |
:math:`s_{{2}_{1}}`  |       |       |     b |       |
---------------------+-------+-------+-------+-------+
:math:`s_{{3}_{0}}`  |       |       |       |  a    |
:math:`s_{{3}_{1}}`  |       |       |       |     c |
---------------------+-------+-------+-------+-------+

Identifying Requirements

Following the consequences of the selection problem, observe, that if s_0₀ is eventually selected, then s_2₀ can no longer be selected, because literal a at position s_2₀, 2₀ conflicts with literal ¬a at position s_0₀, 0₀, therefore, s_2₁ must then be selected to preserve satisfiability.

It makes no difference, whether this required selection is made later as a matter of circumstances, or if it is promised in advance by refining partial assignment s_0₀ with literal b at position s_0₀, 2₁:

---------------------+-------+-------+-------+-------+
:math:`s_{{0}_{0}}`  | ¬a    |       |     b |       |
:math:`s_{{0}_{1}}`  |    ¬b |       |       |       |
---------------------+-------+-------+-------+-------+
:math:`s_{{1}_{0}}`  |       | ¬a    |       |       |
:math:`s_{{1}_{1}}`  |       |     d |       |       |
---------------------+-------+-------+-------+-------+
:math:`s_{{2}_{0}}`  |       |       |  a    |       |
:math:`s_{{2}_{1}}`  |       |       |     b |       |
---------------------+-------+-------+-------+-------+
:math:`s_{{3}_{0}}`  |       |       |       |  a    |
:math:`s_{{3}_{1}}`  |       |       |       |     c |
---------------------+-------+-------+-------+-------+

By analogy, the same is true for conflicting selections s_2₀ and s_0₀:

---------------------+-------+-------+-------+-------+
:math:`s_{{0}_{0}}`  | ¬a    |       |     b |       |
:math:`s_{{0}_{1}}`  |    ¬b |       |       |       |
---------------------+-------+-------+-------+-------+
:math:`s_{{1}_{0}}`  |       | ¬a    |       |       |
:math:`s_{{1}_{1}}`  |       |     d |       |       |
---------------------+-------+-------+-------+-------+
:math:`s_{{2}_{0}}`  |    ¬b |       |  a    |       |
:math:`s_{{2}_{1}}`  |       |       |     b |       |
---------------------+-------+-------+-------+-------+
:math:`s_{{3}_{0}}`  |       |       |       |  a    |
:math:`s_{{3}_{1}}`  |       |       |       |     c |
---------------------+-------+-------+-------+-------+

Distributive expansion of clauses S₀, S₂ shows, that this is exactly what will happen:

( ¬a ∨ ¬b ) ∧ ( a ∨ b )
= (( ¬a ∧ ( a ∨  b )) ∨ ( ¬b ∧ ( a ∨  b )))
= ( ¬a ∧ a ) ∨ ( ¬a ∧ b ) ∨ ( ¬b ∧ a ) ∨ ( ¬b ∧ b )
=              ( ¬a ∧ b ) ∨ ( ¬b ∧ a )

Determining the complete set of satisfying assignments is equivalent to distributive expansion of the entire CNF formula P, which generates the set of prime implicants I for a formula P, where each I extends to one or more satisfying assignments.

Therefore performing partial distributive expansion facilitates obtaining the complete set of satisfying assignments for a proposisitional problem in CNF.

Requirement Propagation Round 1

Proceeding further, SM is transformed to:

---------------------+-------+-------+-------+-------+
:math:`s_{{0}_{0}}`  | ¬a    |       |     b |     c |
:math:`s_{{0}_{1}}`  |    ¬b |       |  a    |       |
---------------------+-------+-------+-------+-------+
:math:`s_{{1}_{0}}`  |       | ¬a    |     b |     c |
:math:`s_{{1}_{1}}`  |       |     d |       |       |
---------------------+-------+-------+-------+-------+
:math:`s_{{2}_{0}}`  |    ¬b |     d |  a    |       |
:math:`s_{{2}_{1}}`  | ¬a    |       |     b |       |
---------------------+-------+-------+-------+-------+
:math:`s_{{3}_{0}}`  |    ¬b |     d |       |  a    |
:math:`s_{{3}_{1}}`  |       |       |       |     c |
---------------------+-------+-------+-------+-------+

SM is equivalent to the region of clause conflict sub-matrixes [S_0₀, S_3₃] of the following satoku matrix:

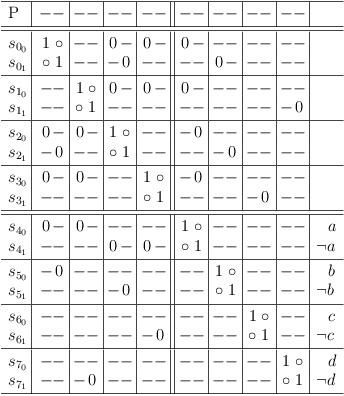
Requirement Propagation Round 2

Observe, that partial assignment s_0₁, which requires partial assignment s_2₀ is no longer consistent, since s_2₀ has been refined with d from s_1₁, 1₁ by the first round of partial distributive expansion. It is therefore necessary to refine s_0₁ with d at position s_0₁, 1₁ also:

---------------------+-------+-------+-------+-------+
:math:`s_{{0}_{0}}`  | ¬a    |       |     b |     c |
:math:`s_{{0}_{1}}`  |    ¬b |     d |  a    |       |
---------------------+-------+-------+-------+-------+
:math:`s_{{1}_{0}}`  |       | ¬a    |     b |     c |
:math:`s_{{1}_{1}}`  |       |     d |       |       |
---------------------+-------+-------+-------+-------+
:math:`s_{{2}_{0}}`  |    ¬b |     d |  a    |       |
:math:`s_{{2}_{1}}`  | ¬a    |       |     b |       |
---------------------+-------+-------+-------+-------+
:math:`s_{{3}_{0}}`  |    ¬b |     d |       |  a    |
:math:`s_{{3}_{1}}`  |       |       |       |     c |
---------------------+-------+-------+-------+-------+

Following all consequences, SM is transformed to:

---------------------+-------+-------+-------+-------+
:math:`s_{{0}_{0}}`  | ¬a    |       |     b |     c |
:math:`s_{{0}_{1}}`  |    ¬b |     d |  a    |       |
---------------------+-------+-------+-------+-------+
:math:`s_{{1}_{0}}`  | ¬a    | ¬a    |     b |     c |
:math:`s_{{1}_{1}}`  |       |     d |       |       |
---------------------+-------+-------+-------+-------+
:math:`s_{{2}_{0}}`  |    ¬b |     d |  a    |       |
:math:`s_{{2}_{1}}`  | ¬a    |       |     b |     c |
---------------------+-------+-------+-------+-------+
:math:`s_{{3}_{0}}`  |    ¬b |     d |  a    |  a    |
:math:`s_{{3}_{1}}`  |       |       |       |     c |
---------------------+-------+-------+-------+-------+

which is equivalent to the region of clause conflict sub-matrixes [S_0₀, S_3₃] in the following satoku matrix:

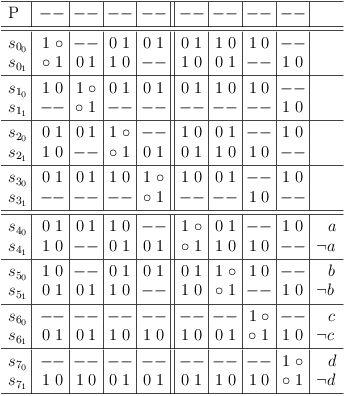
Relation Between Partial Assignments and CNF

Translating SM into a propositional formula PM renders a conjunction of disjunctions of partial assignments s_{i_j}:

(( ¬a ∧  b ∧  c ) ∨ (  a ∧ ¬b ∧  d )) ∧
(( ¬a ∧  b ∧  c ) ∨ (  d )) ∧
((  a ∧ ¬b ∧  d ) ∨ ( ¬a ∧  b ∧  c )) ∧
((  a ∧ ¬b ∧  d ) ∨ (  c )) ∧

Induction over the full truth table shows that P and PM are logically equivalent. And since that is so, it is irrelevant to propose a logical difference between CNF and a conjunction of DNFs.

Relation Between Partial Assignments and Prime Implicants

It is obvious, that each of the prime implicants I:

( ¬a ∧  b ∧  c )
(  a ∧ ¬b ∧  d )

obtained by a full distributive expansion of PM must necessarily be a conjunction s_{i_j}∧..∧s_{f_g} of at least 2 non-conflicting partial assignments from PM.

Reliable Assignments

Under certain conditions, the set of partial assignments s_{i_j} represents a set RA of reliable assignments r, which are guaranteed to extend to a satisfying assignment under all branches of DPLL. I.e., DPLL can never resolve an empty clause.

For a 2-SAT problem, the conditions are met as soon as the partial distributive expansion is fully completed. A 2-SAT problem is also trivially satisfiable, if the partial distributive expansion does not produce 2 contradictions in a single clause.

Satoku Matrix

The satoku matrix processes propositional problems by mapping propositional formulas specified as a conjunction of arbitrary DNFs to the equivalent selection problem in an inverted adjacency matrix. It further abstracts propositional variables to special cases of 2-literal clauses (p∨¬p).

It is obvious, that graph theory is necessary to describe the satoku matrix, but not sufficient to describe partial distributive expansion as it lacks the necessary expressiveness in regard to clause constraints of CNF formulas. The atoms of the satoku matrix are not vertices, but vertex clusters including edges. A variety of subatomic particles includes edge clusters, partial assignments (aka. selections). The ambiguity of propositional variables is permanently exposed instead of hidden behind the necessity that a decision has to be made eventually.

It is obvious, that propositional logic is sufficient and necessary to describe the satoku matrix, but it lacks the necessary expressiveness to describe partial distributive expansion in a simple and intuitive manner. It also lacks the connectivity and transformative power of a graph.

Many observations made in the context of the satoku matrix are very hard to deduce in both graph theory and propositional logic alone. However, none of those observations violates established knowledge in these fields.

For example, the mentioned set RA of reliable assignments does not appear from refinement of partial assignments, unless partial distributive expansion is performed in the exact manner described above. There is also no incentive to construct RA by further minimizing prime implicants due to the exponential time complexity of the algorithm. A full verification of the reliability property also has exponential time complexity (although far less than a full distributive expansion). Therefore this useful property obviously remains undetected, until deduction from the state of the satoku matrix insistently suggests, that the reliable assignment presented must actually be necessary and sufficient to solve the problem.

Another counter-intuitive effect is that nogoods are actually highly desired in the context of the satoku matrix. Because they appear only as a result of necessary deductions, they reduce the problem size, which is a good thing. There is no back-tracking in the traditional sense in the satoku matrix, unless a selection or decision algorithm is implented on top of it.

The consequences from the illusionary notions of both well-defined CNFs and atomic propositional variables are especially hard to understand without the transformational power of the satoku matrix.

Copyright